Trigonometric Levelling  

• It is an indirect method of levelling in which the relative elevation of various points are determined from vertical angle and horizontal distance measured with a theodolite and tape / chain /  Tacheometer respectively.
• It is not as accurate as direct leveling but can be used for topographic work or where direct levelling is not possible.
• This technique if levelling work is usual to find a RL of any point which has elevation is very high / low.
• In these techniques after setting the instrument at any location first back sight reading is taken then angle of elevation is measured to the target.

1.Determination of elevation of object when its base is accessible.

Let the base B of the any structure (like: tower, chimney, etc) is accessible, and the horizontal distance D between the instrument station A and the base B can be measured using a tape. Let Q be the top of structure whose elevation is to be calculated.

Set up the theodolite over A. Take a backsight on the B.M. and determine the height of instrument(s).

R.L. of the line of collimation  = R.L. of B.M. + s

If the line of collimation intersects the structure at Q. the distance PQ’ is same as the horizontal distance D.

Sight the top of the chimney, and measure the angle of elevation θ.

In the triangle PQQ’.

QQ’=Dtanθ

h = Dtanθ

R.L of the top of the structure = R.L. of B.M. + s + Dtanθ.

2.Determination of elevation of object when its base is not accessible.

In this case instrument shift at two known locations and staff reading are taken to the Benchmark (BM) and vertical angle is measured to the target from both stations.

All three points [A, B, C] are in the same vertical plane.

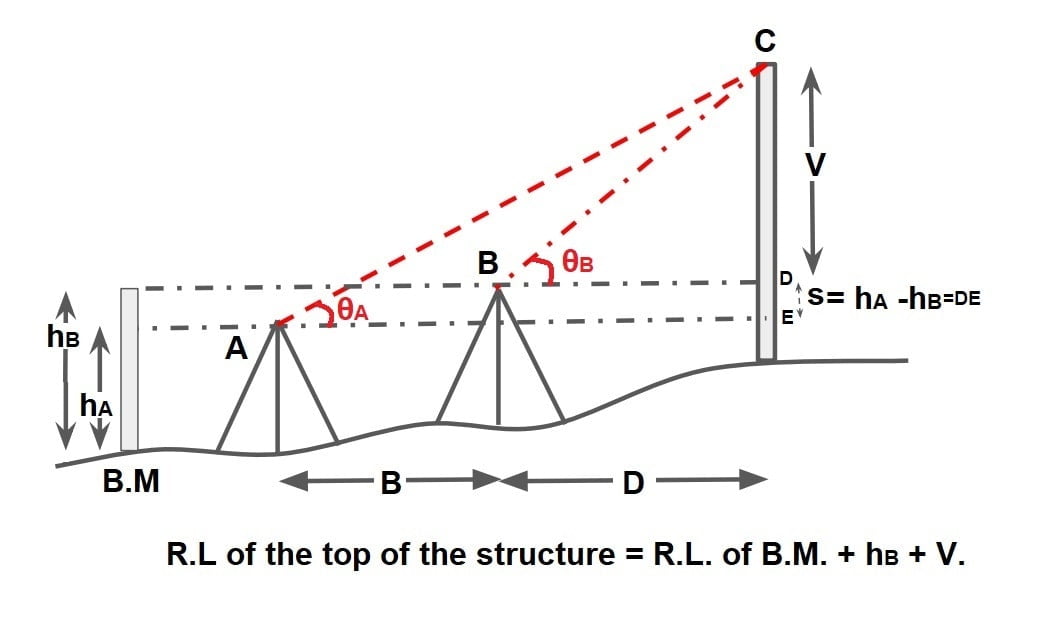
from Δ ACE

CE = AE⋅tanθ_A

(V+S)= (B+D)⋅tanθ_A   ….(1)

from Δ BCD

CD = BD⋅tanθB

V= D⋅tanθB   ….(2)

In equation 1 & 2, V & D are unknow. There are two equation and two unknow so we calculate the value of V & D by solving the equation.

Note:

Higher the angle of elevation near is the instrument to the target.

Higher the back sight reading higher the elevation of the instrument at position.

3.Determination of elevation of the object when the two instruments are not in the same vertical plane.

The instrument stations A and B are not in the same vertical plane. And assume point C is the top point of the object.  The procedure used is as follows:

• Set up the instrument over A. Measure the vertical angle ∠DAC= θ_A, Measure the horizontal angle ∠CAB= α_A.
• Set up the instrument over B. Measure the vertical angle ∠EBC= θ_B, Measure the horizontal angle ∠CBA= α_B.

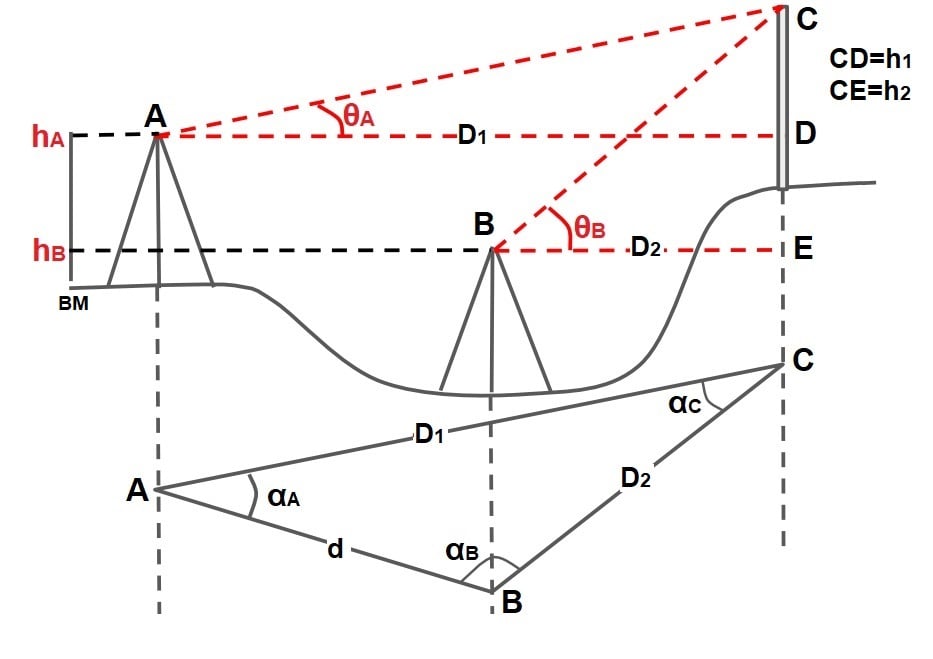
Find the RL of Q

from Δ ACD on vertical plane

CD = AD⋅tanθ_A

h₁= D₁×tanθ_A   ….(1)   {Unknown is h_1, D₁}

from Δ BCE on vertical plane

CE = BE⋅tanθ_B

h₂= D₂×tanθ_B   ….(2)  {Unknown is h_2, D₂}

from Δ ABC on horizontal plane {Unknown is h_2, D₂}

{Unknown is D_1, D_2, & α_C (α_C = 180°-α_A -α_B) }

for D_1, D_2, 

\(\frac{sin\alpha _A}{D_2}=\frac{sin\alpha _B}{D_1}=\frac{sin\alpha _C}{d}\) …(3)

D_{1, &} D_2, is calculated by equation 3. And for find the value of h_1, put the value of D₁ in equation 1. Same procedure for find the value of h_2, put the value of D₂ in equation 2.

RL of Q = RL of BM + h_A + h₁

h_A =staff reading at BM when the instrument is at A

For checking purpose

RL of Q = RL of BM + h_B + h₂

h_B =staff reading at BM when the instrument is at B

FOR MORE INFORMATION ABOUT SURVEYING