Specific Energy in Open Channel Flow
⇒ The total energy of the channel with respect to datum is given by
H = z + y·cosθ + α·v2/2g
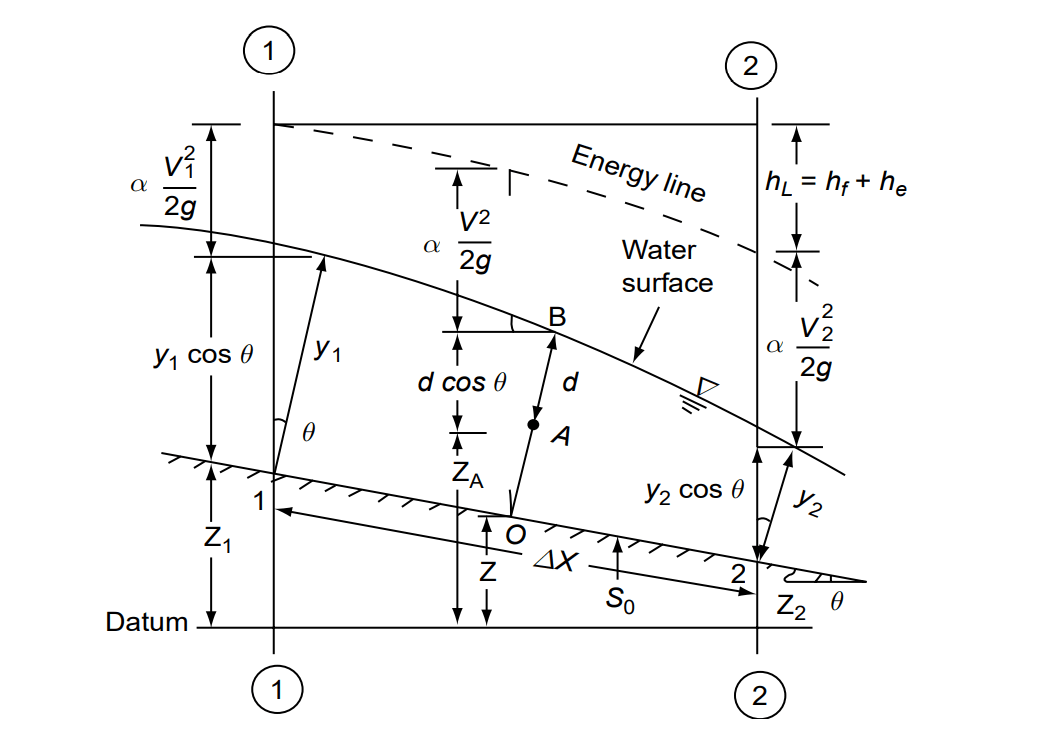
⇒ If datum is considered to be channel bottom, then energy with respect to channel bottom/datum is termed as “Specific Energy (E)”.
E= y·cosθ + α·v2/2g
⇒ If flow is turbulent (α=1).
E= y·cosθ+ v2/2g
⇒ If channel bottom is horizontal, θ= 0° so cosθ=1.
E= y + v2/2g
where, y= normal depth or depth of flow section, v= mean velocity of flow.
Note: If vertical depth or depth of flow is given, normal depth = vertical depth×cosθ.
⇒ The total energy in a real fluid always decreases in the direction of flow/downstream direction in order to overcome the resistance offered by friction & channel boundaries.
⇒ But specific energy is constant for uniform flow & can either decrease or increase in case of varied flow.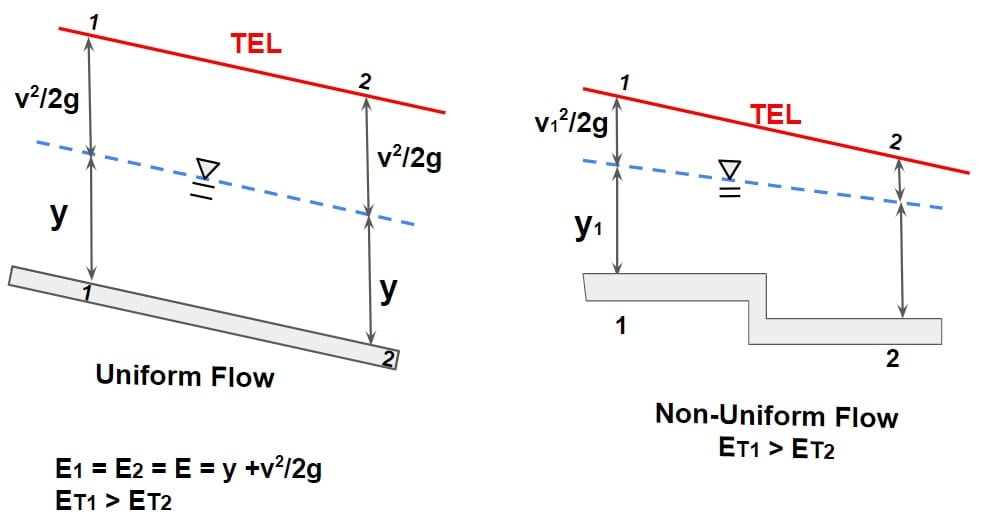
⇒ In frictionless channel total energy is constant the specific energy is varies. The specific energy will be constant if the channel bed is horizontal. 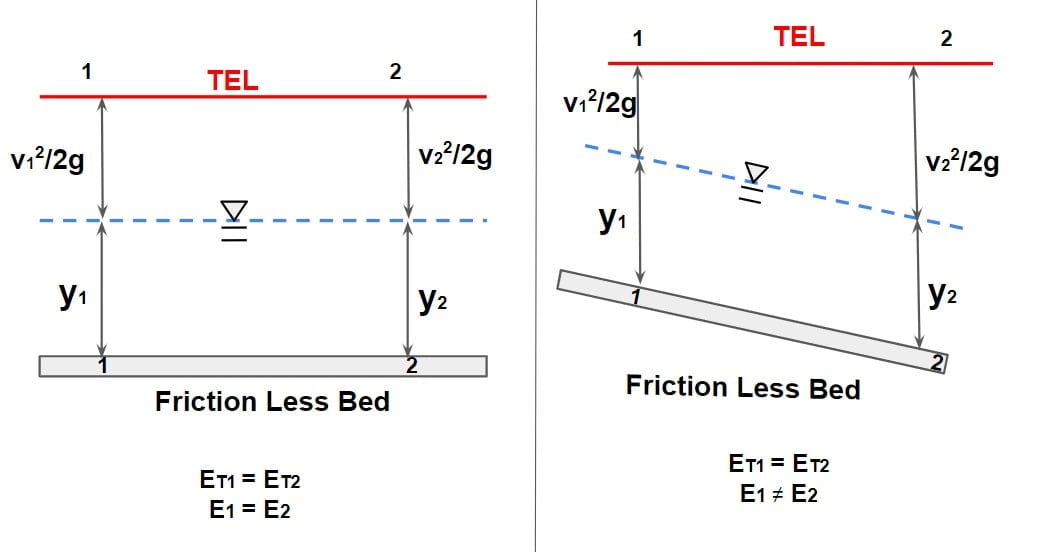
ET= Total Energy, E= Specific Energy
Relationship Between Specific Energy and Depth of Flow (Energy Depth Relationship)
Case.1 When Discharge is Constant
\(E=y+\frac{v^{2}}{2g}\)
\(E=y+\frac{(Q/A)^{2}}{2g}\)
\(E=y+\frac{Q^{2}}{2gA^{2}}\)
⇒ From above relationship it can be inferred that
E= ƒ(y,Q)
⇒ If discharge is kept constant specific energy varies with depth of flow cubically. (The above equation is a cubic parabola equation.)
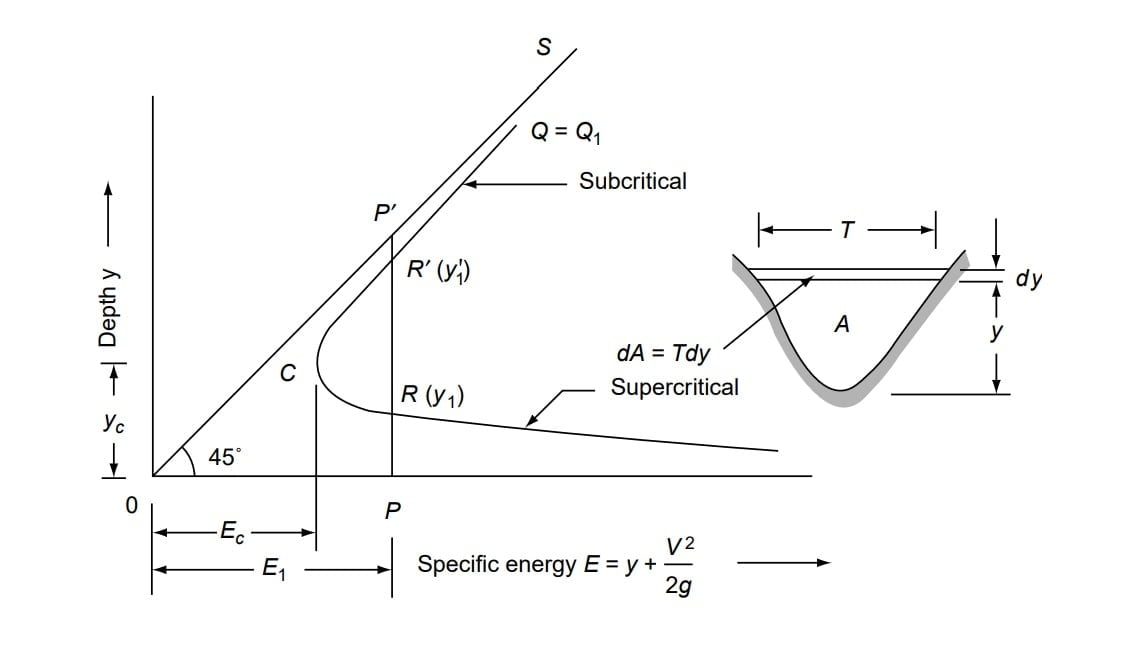
\(E=y+\frac{Q^{2}}{2gA^{2}}\)
⇒ The above equation of cubic parabola have two positive roots for the given value of E.
⇒ Hence, it can be stated that for a given discharge passing through a section, there can be two depth in the channel section having same specific energy(E1).
⇒ Alternate Depths
⇒ These two possible depth having the same specific energy are known as ‘Alternate Depths‘.
⇒ A line (OS) having a slope of when drawn from origin, signifies E= pressure head + kinetic head. (\(E=y+\frac{Q^{2}}{2gA^{2}}\))
⇒ The upper limb of specific energy curve is asymptote to this line OS.
⇒ As shown in the above figure for specific energy E there are two depths of flow.
if, depth of flow, y1 = PR
then, velocity head = RP’
also,
if, depth of flow, y’1 = PR’
then, velocity head = R’P’
⇒ If pressure head is more y’1>y1 then kinetic head corresponding to it v’12/2g ( R’P’) <v12/2g (RP’) would be comparatively less.
⇒ With increase in specific energy (E1), difference between alternate depth (y’1-y1) increases & with decrease in specific energy (E1), difference between alternate depth (y’1-y1) decreases.
⇒ The one of the alternate depth y’1 is corresponding to subcritical flow and the other depth y1 is corresponding to super critical flow.
⇒ At certain value of E=Ec, the two alternate depth will merge with each other.
⇒ No value of y can be obtained for E<Ec, denoting the flow under given condition is not possible in this region.
⇒ The condition of minimum specific energy is know as “Critical Flow Condition or Critical State” & the corresponding depth yc is termed as “Critical Depth”.
⇒ At critical depth, the specific energy is minimum. Thus differentiating Equation of “E”
with respect to y (keeping Q constant) and equating to zero,
\(\frac{\mathrm{d} E}{\mathrm{d} y}=0\).
\(E=y+\frac{Q^{2}}{2gA^{2}}\).
\(\frac{\mathrm{d} E}{\mathrm{d} y}=1-\frac{Q^{2}}{gA^{3}}\frac{\mathrm{d} A}{\mathrm{d} y}\)=0.
⇒ But \(\frac{\mathrm{d} A}{\mathrm{d} y}=T\)= top width, i.e. width of the channel at the water surface.
| \(\frac{Q^{2}T}{gA^{3}}=1\) |
Note: If value of α is not unity, then for critical state
| \(\alpha\frac{ Q^{2}T}{gA^{3}}=1\). |
⇒ The critical flow condition is governed only by the channel geometry & discharge and K.E correction factor (α) & is independent of bed slope, roughness of channel section.
From critical state condition, Froude Number will be:
\(\frac{Q^{2}T}{gA^{3}}=1\).
\(\frac{(\frac{Q^{2}}{A^{2}})\times T}{gA}=1\).
\(\frac{v^{2}\times T}{gA}=1\).
\(\frac{v^{2}}{g\frac{A}{T}}=1\).
Taking the square roots
\(\frac{v}{\sqrt{g\frac{A}{T}}}=1\).
we know that
\(F= \frac{v}{\sqrt{gL_c}}\). (\(L_c= \frac{A}{T}\))
\(F= \frac{v}{\sqrt{g\frac{A}{T}}}\).
Fc=1
⇒ So, when the flow is critical flow, Froude Number will be one. ( at the critical flow y = yc
and F = Fc = 1.0)
Note: For a channel with large longitudinal slope θ and having a flow with an energy correction factor of α, the Froude number F will be defined as
\(F=\frac{v}{\sqrt{\frac{gAcos\theta }{\alpha T}}}\).

- If Fr <1: Flow is called sub critical.
- If Fr = 1: Flow is called critical. At critical flow condition specific energy a minimum.
- If Fr >1: Flow is called super critical or shooting flow or torrential flow called rapid flow.
| Type of flow | Depth Of flow | Velocity of Flow | Froude Number |
| Subcritical | y>yc | v<vc | Fr<1 |
| Critical | y=yc | v=vc | Fr=1 |
| Super critical | y<yc | v>vc | Fr>1 |
Note: for non prismatic channel, the channel section varies along the length of the channel and hence, the specific energy differs from section to section.
Case.2 When Discharge is Variable
⇒ In the above section the critical-flow condition was derived by keeping the discharge constant. (If y = constant, and discharge is increase then specific energy is increases. So when discharge is increase then curve shifted to right.)
⇒ The specific-energy diagram can be plotted for different discharges Q1, Q2, …..Qn = constant, as

⇒ The difference between alternate depth decreases [(y2)1-(y1)1 >(y2)2-(y1)2 ] with increase in discharge (Q2> Q1).
⇒ Draw the specific energy curve for Q = Qm such that Q3 < Qm < Q4, This curve will be just tangential to PP’ at Point C.
⇒ Specific energy curve for Q=Qm (Q3 < Qm < Q4), represents the maximum value of discharge that can be passed in the channel while keeping the specific energy at a constant value E₁.
⇒ Specific energy curve for Q> Qm will have no intercept on the line PP’ and hence there will be no depth at which such discharge can be passed in the channel with the given specific energy.
\(E=y+\frac{Q^{2}}{2gA^{2}}\)
\(Q= A\sqrt{2g(E-y)}\)
⇒ The condition for maximum discharge can be obtained by differentiating the Eq. of Q with respect to y and equating it to zero while keeping E = constant.
Thus \(\frac{\mathrm{d} Q}{\mathrm{d} y}=\sqrt{2g(E-y)}\frac{\mathrm{d} A}{\mathrm{d} y}-\frac{gA}{\sqrt{2g(E-y)}}=0\).
by putting, \(\frac{\mathrm{d} A}{\mathrm{d} y}=T\) and \(\frac{Q}{ A}=\sqrt{2g(E-y)}\).
\(\frac{Q}{A}T-\frac{gA\cdot A}{Q}=0\).
\(\frac{Q}{A}T=\frac{gA\cdot A}{Q}\).
\(\frac{Q^{2}T}{gA^{3}}=1\).
⇒ \(\frac{Q^{2}T}{gA^{3}}=1\). corresponds to critical flow condition therefore critical flow condition corresponds to the condition for maximum discharge in a channel for a fixed specific energy.
Note:
\(\frac{Q^{2}T}{gA^{3}}=1\) is the condition such that
- For a given discharge, specific energy to be minimum.
- For a given specific energy, discharge to be maximum.
Critical Depth (yc): Critical depth is defined as that depth of flow of water at which the specific energy is minimum. This is denote by yc.
Critical Velocity (vc): The velocity of flow at the critical depth is know as critical velocity. This is denote by vc.
Calculation of the Critical Depth
\(\frac{Q^{2}T}{gA^{3}}=1\).
Using above equation, expressions for the critical depth in channels of various geometric shapes can be obtained as follows:
Critical Depth of Rectangular Section
For a rectangular section,

A = By and T = B
For critical flow condition,
\(\frac{Q^{2}T}{gA^{3}}=1\).
\(\frac{Q^{2}B}{g(By_c)^{3}}=1\).
\(\frac{Q^{2}B}{gB^{3}y_c^{3}}=1\).
\(y_c^{3}=\frac{Q^{2}}{gB^{2}}\).
Also, if q = discharge per unit width = Q/B,
| \(y_c=(\frac{q^{2}}{g})^{1/3}\)…..(1) |
Specific energy at critical depth “Ec“
\(E_c=y_c+\frac{v_c^{2}}{2g}\).
\(E_c=y_c+\frac{Q^{2}}{2gA^{2}}\).
\(E_c=y_c+\frac{q^{2}}{2g\cdot y_c^{2}}\).
from equation (1) \(g\cdot y_c^{3}=q^{2}\).
\(E_c=y_c+\frac{g\cdot y_c^{3}}{2g\cdot y_c^{2}}\).
\(E_c=y_c+\frac{y_c}{2}\).
| \(E_c=\frac{3}{2}y_c\). |
Note that specific energy at critical depth of flow is independent of width of channel section
Froude number for rectangular channel will be
\(F_r=\frac{v}{\sqrt{g\times \frac{A}{T}}}\).
Since A/T = y, the Froude number for a rectangular channel will be defined as
\(F_r=\frac{v}{\sqrt{g\times y}}\).
For critical flow, Fr= 1
\(1=\frac{v_c}{\sqrt{g\times y_c}}\).
| \(v_c=\sqrt{g\times y_c}\). |
Critical Depth of Triangular Section
For a triangular channel having a side slope of m horizontal: 1 vertical, A=\(A=\frac{1}{2}2my\cdot y\)=my2 and T = 2my.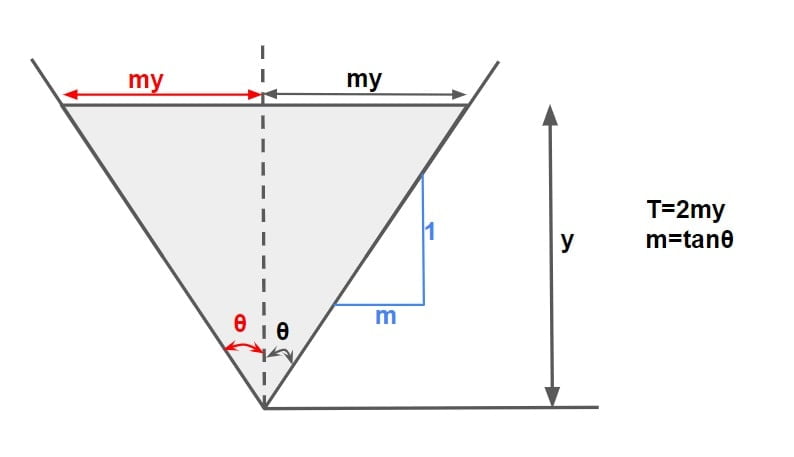
For critical flow condition,
\(\frac{Q^{2}T}{gA^{3}}=1\).
\(\frac{Q^{2}(2my_c)}{g(m\cdot y_c^{2})^{3}}=1\).
\(\frac{2Q^{2}}{g\cdot m^{2}\cdot y_c^{5}}=1\).
| \(y_c=(\frac{2Q^{2}}{gm^{2}})^{1/5}\). m= tanα |
Specific energy at critical depth “Ec“
\(E_c=y_c+\frac{v_c^{2}}{2g}\).
\(E_c=y_c+\frac{Q^{2}}{2gA^{2}}\).
\(E_c=y_c+\frac{\frac{A^{3}}{T}}{2A^{2}}\).
\(E_c=y_c+\frac{A}{2T}\).
\(E_c=y_c+\frac{my_c^{2}}{2\times 2my_c}\).
\(E_c=y_c+\frac{y_c}{4}\).
| \(E_c=1.25y_c\). |
Froude number for rectangular channel will be
\(F_r=\frac{v}{\sqrt{g\times \frac{A}{T}}}\).
\(F_r=\frac{v}{\sqrt{g\times \frac{my^{2}}{2my}}}\).
\(F_r=\frac{\sqrt{2}\cdot v}{\sqrt{g\times y}}\).
\(F_r=\frac{v_c}{\sqrt{g\times \frac{y_c}{2}}}=1\).
for critical flow Fr=1
| \(\frac{\sqrt{2}\cdot v_c}{\sqrt{g\times y_c}}=1\). |
Section Factor Z
The expression \( A\sqrt{A/T}\) is a function of the depth y for a given channel geometry which can be used to simplify the analysis of flow in open channel flow and is known as the section factor (Z).
Thus,
\(Z= A\sqrt{A/T}\).
\(Z_c= A_c\sqrt{A_c/T}\).
Squaring Both Sides
\(Z_c^{2}= \frac{A_c^{3}}{T}\)…..(1)
for critical flow condition
\(\frac{Q^{2}T}{gA^{3}}=1\).
\(\frac{A^{3}}{T}=\frac{Q^{2}}{g}\)……(2)
comparing equation 1 & 2
\(Z_c^{2}=\frac{Q^{2}}{g}\).
| \(Q_c=Z_c\sqrt{g}\) |
Relation Between Discharge & Depth of Flow
For rectangular channel the specific energy equation is
\(E=y+\frac{v^{2}}{2g}\).
Q=v×A,
A=B×y,
q= Q/B, discharge per unit width
\(E=y+\frac{q^{2}}{2g\cdot y^{2}}\).
\(q=\sqrt{2g(E-y)y^{2}}\)
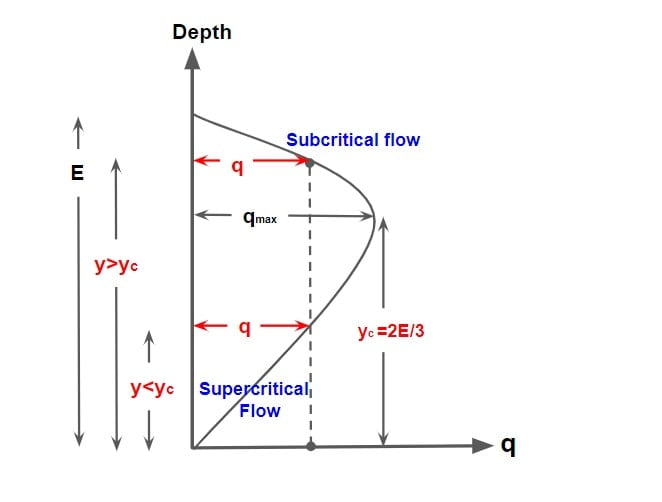
- From the previous discussion we know that at critical flow condition discharge(Q) is maximum.
- Two possible depth of flow are available for a certain value of ‘q’ as long as it is less than qmax.
- At maximum discharge the two depth merge into single depth termed as critical depth ‘yc‘.
- At y<yc, flow is supercritical.
- At y>yc, flow is subcritical.
Question: If y1 & y2 are alternate depth in a rectangular channel, than show that \(y_c=(\frac{2y_1^{2}\cdot y_2^{2}}{y_1+y_2})^{1/3}\) and \(E=\frac{y_1^{2}+y_2^{2}+y_1\cdot y_2}{y_1+y_2}\).
Solution:
At alternate depth, specific energy E= constant.
E= E1 = E2
\(y_1+\frac{v_1^{2}}{2g}=y_2+\frac{v_2^{2}}{2g}\).
\(y_1+\frac{Q^{2}}{2g(By_1)^{2}}=y_2+\frac{Q^{2}}{2g(By_2)^{2}}\).
\(y_1+\frac{q^{2}}{2g(y_1)^{2}}=y_2+\frac{q^{2}}{2g(y_2)^{2}}\).
for rectangular section \(y_c^{3}=\frac{q^{2}}{g}\).
\(y_1+\frac{y_c^{3}}{2(y_1)^{2}}=y_2+\frac{y_c^{3}}{2(y_2)^{2}}\).
\(\frac{y_c^{3}}{2}(\frac{1}{y_1^{2}}-\frac{1}{y_2^{2}})=y_2-y_1\).
| \(y_c=(\frac{2y_1^{2}\cdot y_2^{2}}{y_1+y_2})^{1/3}\). |
specific energy E= E1 = E2
\(E=y_1+\frac{y_c^{3}}{2(y_1)^{2}}\).
\(E=y_1+\frac{2y_1^{2}y_2^{2}}{2(y_1)^{2}(y_1+y_2)}\).
\(E=\frac{y_1(y_1+y_2)+y_2^{2}}{y_1+y_2}\).
| \(E=\frac{y_1^{2}+y_2^{2}+y_1\cdot y_2}{y_1+y_2}\). |
Channel Transition
- A transition is the portion of a channel with varying cross section, which connects one uniform flow channel to another uniform flow channel.
- This variation of a channel section may be caused either by reducing or increasing the width, or by raising or lowering the bottom of the channel.
- Some use of channel transition are measuring of flow, dissipation of energy, reduction or increase of velocities, change in channel section or alignment with minimum of energy dissipation.
- When the change in cross sectional dimensions of the channel occurs in a relatively short length then the transition is termed as sudden transition.
- When the change of cross sectional area of the channel takes place gradually in a relatively long length of channel then the transition is termed as gradual transition.
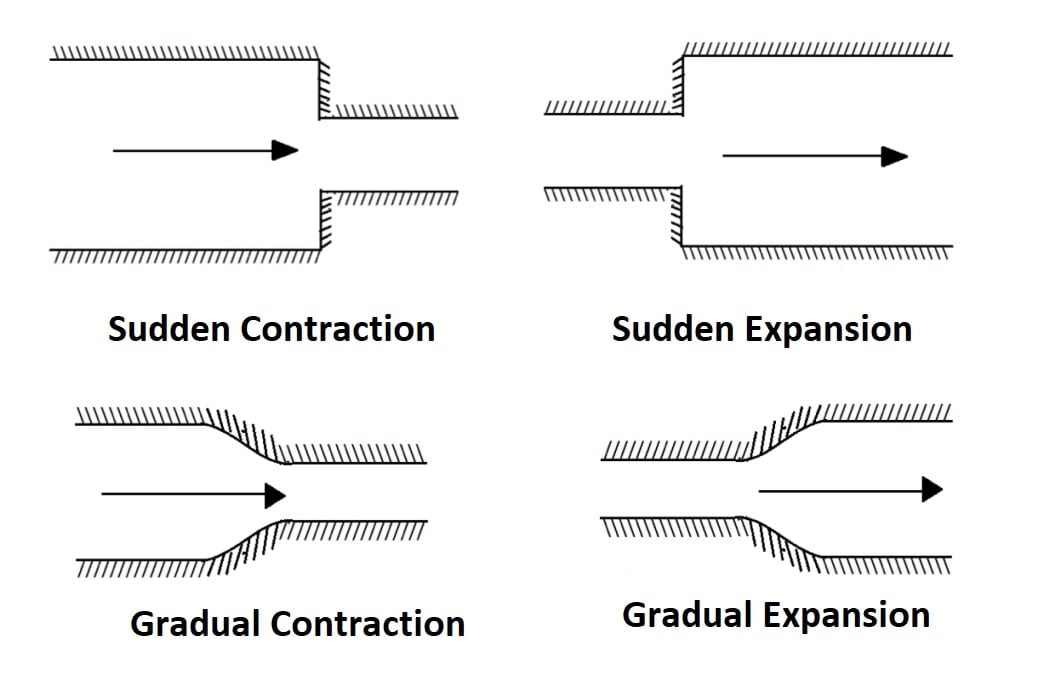
- The concept of specific energy and critical depth are extremely useful in analysis of problems associated with channel transitions.
- While analyzing channel transition following assumptions are made.
- Channel bed is horizontal and frictionless i.e. TEL will be parallel to the channel bed.
- There is no loss of energy takes place between any two section in channel.
Channel with a Hump (Flow Transition Due to Hump Creations)
- We are considering the situation in which flow has been already established after creation of disturbance. hence discharge is same after established of flow equal to discharge before disturbance.
- Nature of flow (subcritical/ super critical) is first find out.
- If the flow is initially sub critically it is assumed that after the disturbance it will remain subcritical at almost become critical. similar will be case for super critical.
1. Subcritical Flow
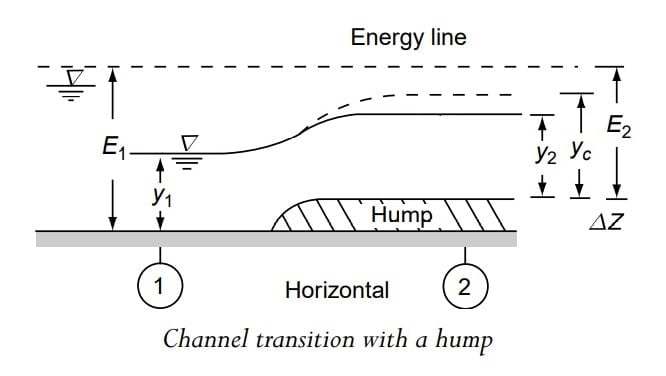
Consider a horizontal, frictionless rectangular channel of width B carrying Q at a depth y1.
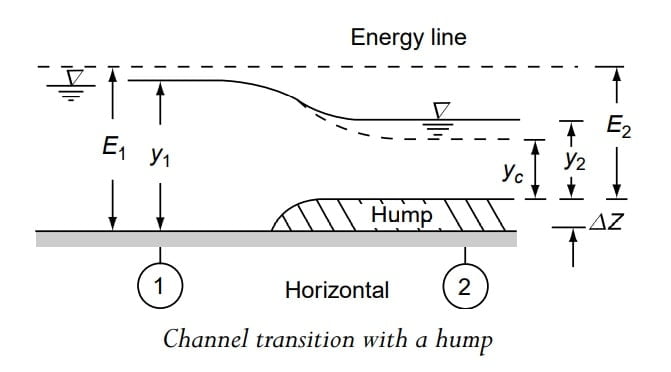 Provided with a rise in bottom of the channel bed termed as ‘Hump’. And the height of hump is Δz.
Provided with a rise in bottom of the channel bed termed as ‘Hump’. And the height of hump is Δz.
There are no energy loss between section (1) and (2).
Construction of a hump causes the specific energy at Section (2) to decrease by Δz.
Thus the specific energies at Sections 1 and 2 are given by
\(E_1=y_1+\frac{v_1^{2}}{2g}\).
\(E_2=E_1-\Delta z\).
E2 < E1
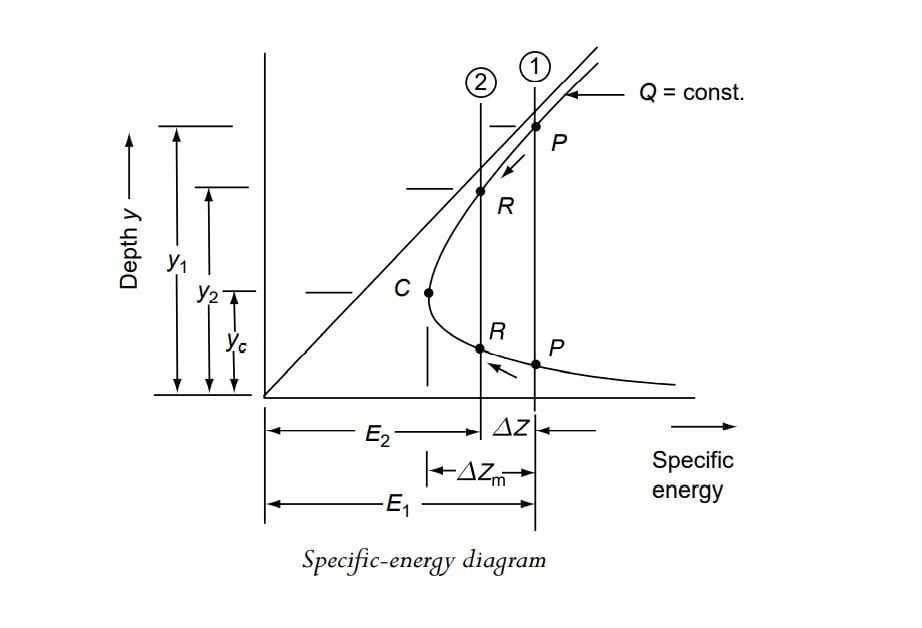
From the specific energy curve it is clear that in case of subcritical flow, as the specific energy decreases, the depth of flow decreases, so y2 is less than y1. (y2 < y1)
Δz can be increased upto that value at which specific energy (E2) reached its critical value (Ec), i.e the minimum value of y2 can be yc.
Let Δzm be the maximum height the hump. the condition at Δzm is given by the relation
E1 – Δzm =E2 = Ec
We know that for rectangular channel \(E_c=\frac{3}{2}y_c\).
so
\(E_2=\frac{3}{2}y_c\). (max height of hump)
What happens when hump is increases such that Δz’ > Δzm.
If the height of the hump is increased further such that Δz’ > Δzm, flow will not occurs because minimum energy required is not there (E2 < Ec) that is choking condition how ever flow pattern will change and E1 become E1‘ = Ec +Δz‘ such that at section (2) energy is Ec.
If Δz’ > Δzm
Ec = E1 – Δzm
E2 = E1 – Δz’
E2 <Ec
So Flow condition is choked.
After establishment of flow downstream condition will become critical & u/s condition will change such that
E2 =Ec & E1‘ = Ec +Δz‘.
y2 =yc & y1‘>y1
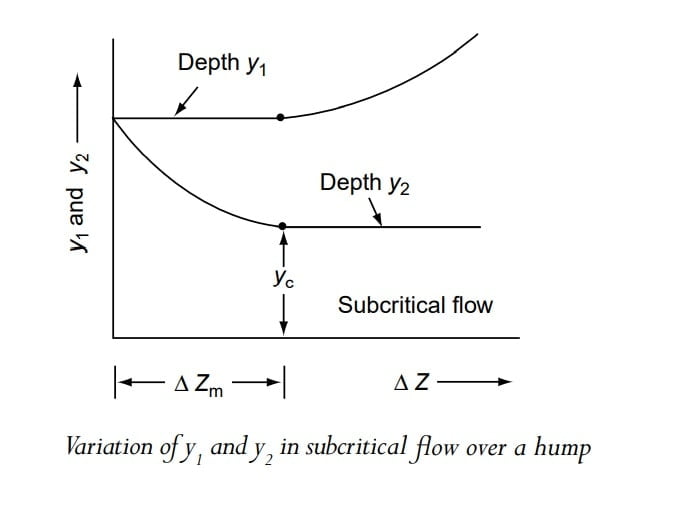
Summarizing all the various sequences for subcritical flow, when 0<Δz <Δzmax the upstream water level remains stationary at y1, while the depth of flow at section 2 decreases with y reaching a minimum value of yc, at Δz =Δzmax, With further increase in the value of Δz, i.e Δz’>Δzm, y2 will continue to remain at yc and y1 will increase to y’1 to have higher specific energy E1.
2. Super Critical Flow
 If the flow is super critical, from the specific energy curve it is clear that in case of super critical flow, as the specific energy decreases, the depth of flow increases, so y2 is more than y1. (y2 > y1)
If the flow is super critical, from the specific energy curve it is clear that in case of super critical flow, as the specific energy decreases, the depth of flow increases, so y2 is more than y1. (y2 > y1)
\(E_1=y_1+\frac{v_1^{2}}{2g}\).
\(E_2=E_1-\Delta z\).
E2 < E1
y2 > y1

The maximum height of the hump (Δzm) can be provided upto that value at which specific energy (E2) reached its critical value (Ec), i.e y2 can be yc.
E1 – Δzm =E2 = Ec
What happens when hump is increases such that Δz’ > Δzm.
If the height of the hump is increased further such that Δz’ > Δzm, flow will not occurs because minimum energy required is not there (E2 < Ec) that is choking condition how ever flow pattern will change and E1 become E1‘ = Ec +Δz‘ such that at section (2) energy is Ec.
If Δz’ > Δzm
Ec = E1 – Δzm
E2 = E1 – Δz’
E2 <Ec
So Flow condition is choked.
After establishment of flow downstream condition will become critical & u/s condition will change such that
E2 =Ec & E1‘ = Ec +Δz‘.
y2 =yc & y1‘<y1
Summarizing all the various sequences for super critical flow, when 0<Δz <Δzmax the upstream water level remains stationary at y1, while the depth of flow at section 2 increases with y reaching a value of yc, at Δz =Δzmax, With further increase in the value of Δz, i.e Δz’>Δzm, y2 will continue to remain at yc and y1 will decrease to y’1 to have higher specific energy E1.
Size of Maximum Hump For Critical Flow
Relation between specific energies at a section upstream of hump (E1) and at the section on the hump (E2) is given as
E1 =E2 + Δz
if Δz= Δzmax , then E2 =Ec
E1 =Ec + Δzmax
Δzmax =E1 -Ec
We know that for rectangular channel \(E_c=\frac{3}{2}y_c\).
| \(\Delta z_m=E_1-\frac{3}{2}y_c\) |
Energy Loss due to Hump
- If there is a energy loss taking place between upstream and down stream sections equal to hL. We can consider a new hump of height (Δz+ hL) in place of original hump of Δz and proceed the calculation. .
- New specific energy equation will be
E1 =E2 +Δz+ hL
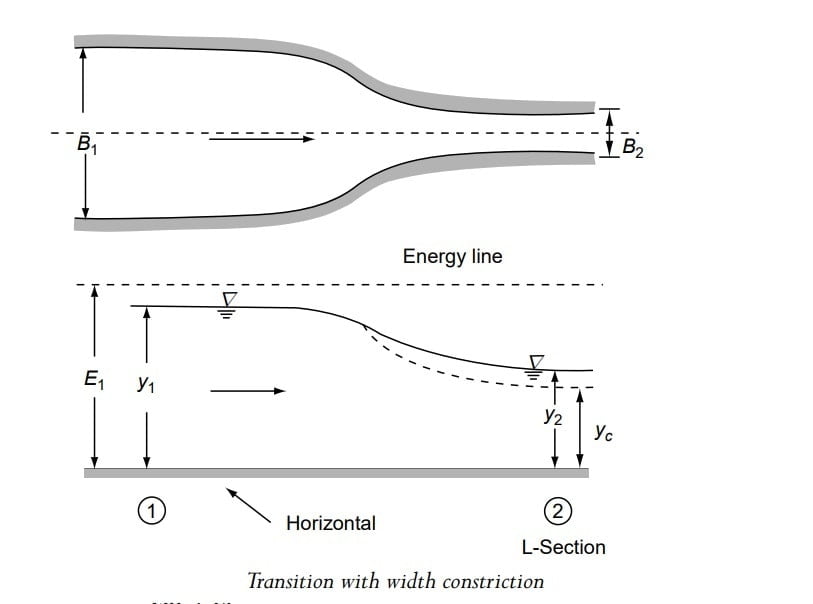
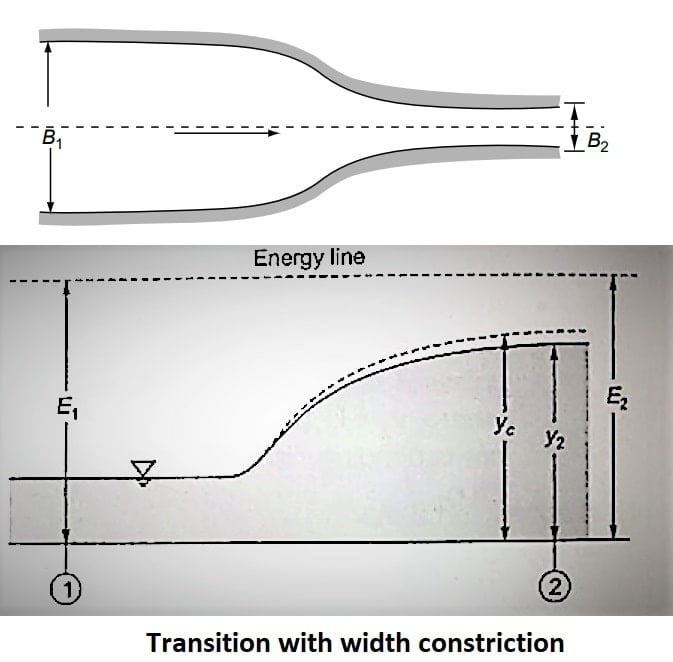
Transition With Reduction of Width in a Rectangular Channel (Flow Transition Due to Width Contraction)
Consider a friction less horizontal channel of width B1, carrying a discharge Q at a depth of flow y1. At section 2 the channel width is been reduced to B2, by a smooth transition.
As there are no energy losses involved and since bed elevations are same at section 1 and section 2, the specific energy at both the section is same.
As the total discharge Q remains same between section 1 and 2. But discharge per unit width changes between section 1 and section 2.
Discharge per unit width at section 1 (B=B1), q1 = Q/B1
Discharge per unit width at section 2 (B=B2), q₂ = Q/B2
∴ Q = Constant and B1 > B2.
∴ q1 < q2
Further if width of section is reduced to B3 < B2 min, the discharge per unit width would further increased.
1. Subcritical Flow
As the approaching flow at section 1 is in subcritical state and depth of flow y1, discharge per unit width q1 = Q/B1.
At section 2, width of section gets reduced to B2, and hence discharge per unit width increase to q1<q2.
 It is observed that for subcritical state of flow if discharge per unit width of flow increases, the depth of flow will decrease.
It is observed that for subcritical state of flow if discharge per unit width of flow increases, the depth of flow will decrease.
Therefore now new depth of flow at section 2 will be y2 <y1.
E1 = E2
\(q_1=\frac{Q}{B_1}\) &\(q_2=\frac{Q}{B_2}\)
y2 <y1
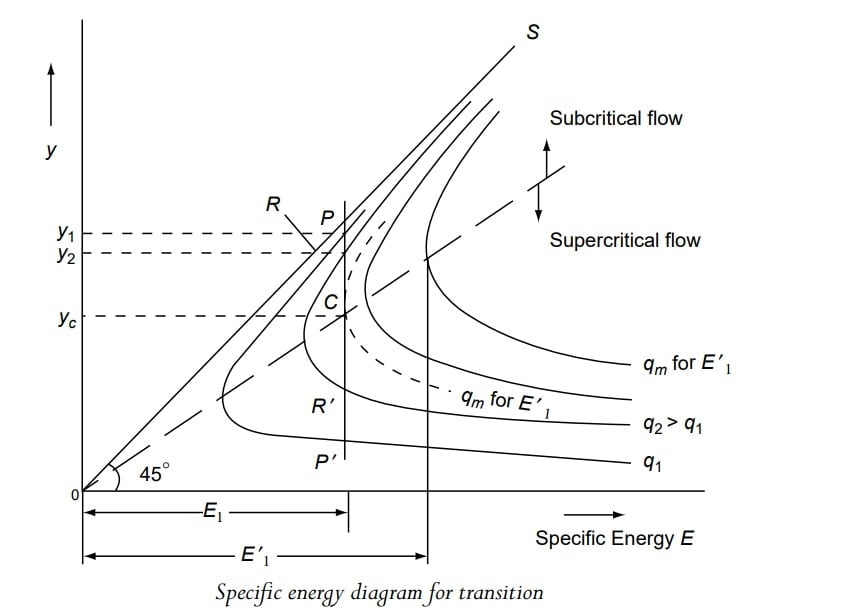
If width is reduced at section 2-2, discharge per unit width would increase but depth will decrease.
This depth of flow decreases upto a certain minimum value “yc” corresponding to which discharge per unit width is max (qmax) & width of throat would be min “B2 min“.
At B2 min, \(q_{max}=\frac{Q}{B_{2 min}}\)
such that E1 =E2 = Ec
Any further q beyond qmax is not possible for same value of specific energy E & this condition is termed as chocking condition .
At chocking condition
y2 =yc
We know that for rectangular channel \(E_c=\frac{3}{2}y_c\).
so
\(y_2=y_c=\frac{2}{3}E_c\).
also we know that for rectangular channel \(y_c=(\frac{q^{2}}{g})^{1/3}\). here for critical flow q= qmax = (Q/B2min).
so \(y_c=(\frac{q_{max}^{2}}{g})^{1/3}\).
\(y_c=(\frac{Q^{2}}{B_{2 min}^{2}g})^{1/3}\).
\(y_c^{3}=\frac{Q^{2}}{B_{2 min}^{2}g}\).
\(B_{2 min}^{2}=\frac{Q^{2}}{y_c^{3}g}\).
\(B_{2 min}=\sqrt{\frac{Q^{2}}{y_c^{3}g}}\).
we know \(y_c=\frac{2}{3}E_c\).
\(B_{2 min}=\sqrt{\frac{27Q^{2}}{8gE_c^{3}}}\).
or
\(B_{2 min}=\sqrt{\frac{27Q^{2}}{8gE_1^{3}}}\).
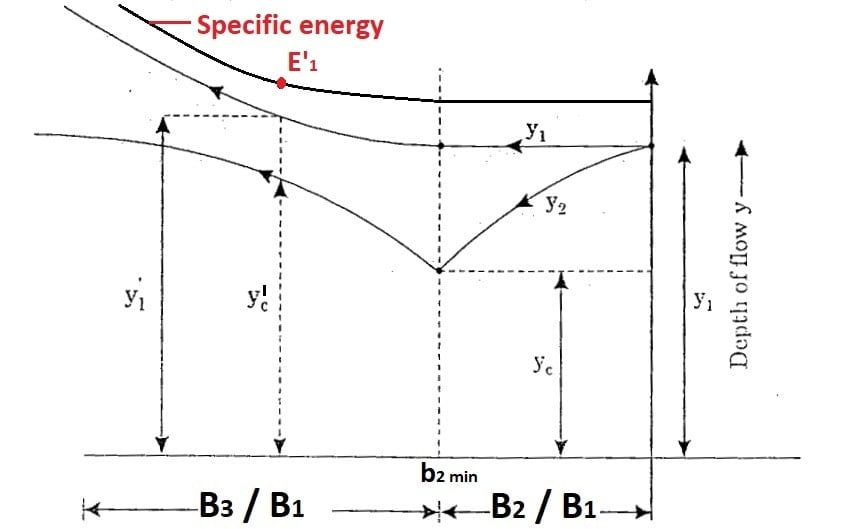
In case of subcritical flow, when width of section 2-2 is reduced further B3< B2min where q3 = qmax’ > qmax , to pass this discharge, specific energy at section 1-1 ‘E1‘ is to be increased. (E1‘>E1).
This results in increase in depth of flow at section 1-1 (y1‘> y1).
The flow at section 2-2, would still remain critical but depth of flow for this new critical state would increase(yc‘>yc).
\({y_2}’={y_c}’=(\frac{q_{3}^{2}}{g})^{1/3}\).
where q3= Q/B3
and E1‘ =E2‘ =Ec‘
where \({E_c}’=\frac{3}{2}(\frac{q_3^{2}}{g})^{1/3}\).
for y1‘
\({E_1}’={y_1}’+\frac{Q^{2}}{2g(B_1^{2}\cdot y_1’^{2})}\).
Here by we can conclude that in subcritical state of flow if width of the throat section b3 <bmin there will be critical flow at section 2 such that new critical depth of flow y’c, will be greater than previous critical depth of flow yc. At section 1 also new depth of flow y’1 >y1, (previous depth of flow for q=qmax).
The variation of y1, y2, with B is shown schematically in figure below.
 2. Supercritical Flow
2. Supercritical Flow
As the approaching flow at section 1 is in supercritical state and depth of flow y1, discharge per unit width q1 = Q/B1.
At section 2, width of section gets reduced to B2, and hence discharge per unit width increase to q1<q2.
 It is observed that for supercritical state of flow if discharge per unit width of flow increases, the depth of flow will increase.
It is observed that for supercritical state of flow if discharge per unit width of flow increases, the depth of flow will increase.
Therefore now new depth of flow at section 2 will be y2 >y1.
E1 = E2
\(q_1=\frac{Q}{B_1}\) &\(q_2=\frac{Q}{B_2}\)
y2 >y1
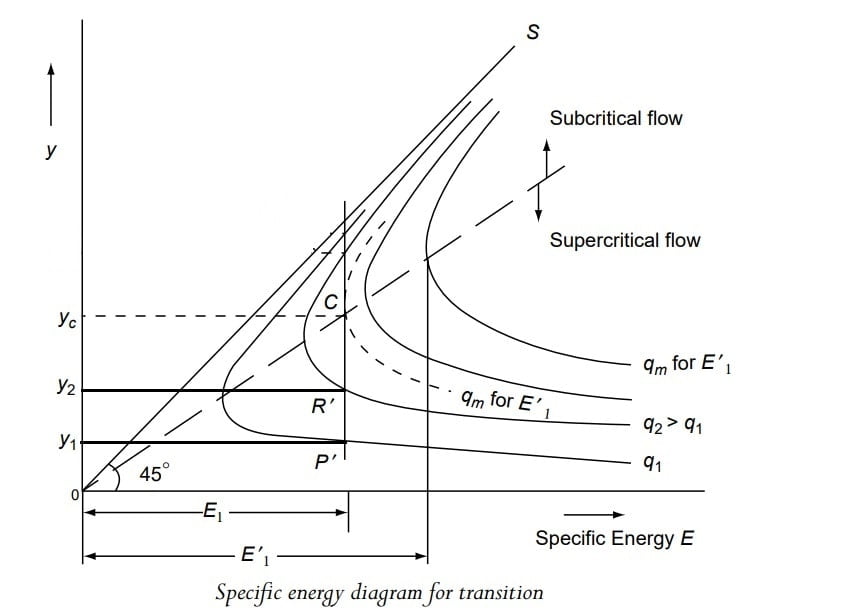
If width is reduced at section 2-2, discharge per unit width would increase, also depth will increase.
This depth of flow increase upto “yc” corresponding to which discharge per unit width is max (qmax) & width of throat is min “B2 min“.
At B2 min, \(q_{max}=\frac{Q}{B_{2 min}}\)
such that E1 =E2 = Ec
Any further q beyond qmax is not possible for same value of specific energy E & this condition is termed as chocking condition .
At chocking condition
y2 =yc
We know that for rectangular channel \(E_c=\frac{3}{2}y_c\).
so
\(y_2=y_c=\frac{2}{3}E_c\).
also we know that for rectangular channel \(y_c=(\frac{q^{2}}{g})^{1/3}\). here for critical flow q= qmax = (Q/B2min).
so \(y_c=(\frac{q_{max}^{2}}{g})^{1/3}\).
\(y_c=(\frac{Q^{2}}{B_{2 min}^{2}g})^{1/3}\).
\(y_c^{3}=\frac{Q^{2}}{B_{2 min}^{2}g}\).
\(B_{2 min}^{2}=\frac{Q^{2}}{y_c^{3}g}\).
\(B_{2 min}=\sqrt{\frac{Q^{2}}{y_c^{3}g}}\).
we know \(y_c=\frac{2}{3}E_c\).
\(B_{2 min}=\sqrt{\frac{27Q^{2}}{8gE_c^{3}}}\).
or
\(B_{2 min}=\sqrt{\frac{27Q^{2}}{8gE_1^{3}}}\).
In case of supercritical flow, when width of section 2-2 is reduced further B3< B2min where q3 = qmax’ > qmax , to pass this discharge, specific energy at section 1-1 ‘E1‘ is to be increased. (E1‘>E1).
This results in increase in depth of flow at section 1-1 (y1‘< y1).
The flow at section 2-2, would still remain critical but depth of flow for this new critical state would increase(yc‘>yc).
\({y_2}’={y_c}’=(\frac{q_{3}^{2}}{g})^{1/3}\).
where q3= Q/B3
and E1‘ =E2‘ =Ec‘
where \({E_c}’=\frac{3}{2}(\frac{q_3^{2}}{g})^{1/3}\).
for y1‘
\({E_1}’={y_1}’+\frac{Q^{2}}{2g(B_1^{2}\cdot y_1’^{2})}\).
Here by we can conclude that in supercritical state of flow if width of the throat section b3 <bmin there will be critical flow at section 2 such that new critical depth of flow y’c, will be greater than previous critical depth of flow yc. At section 1 also new depth of flow y’1 <y1, (previous depth of flow for q=qmax).
The variation of y1, y2, with B is shown schematically in figure below.
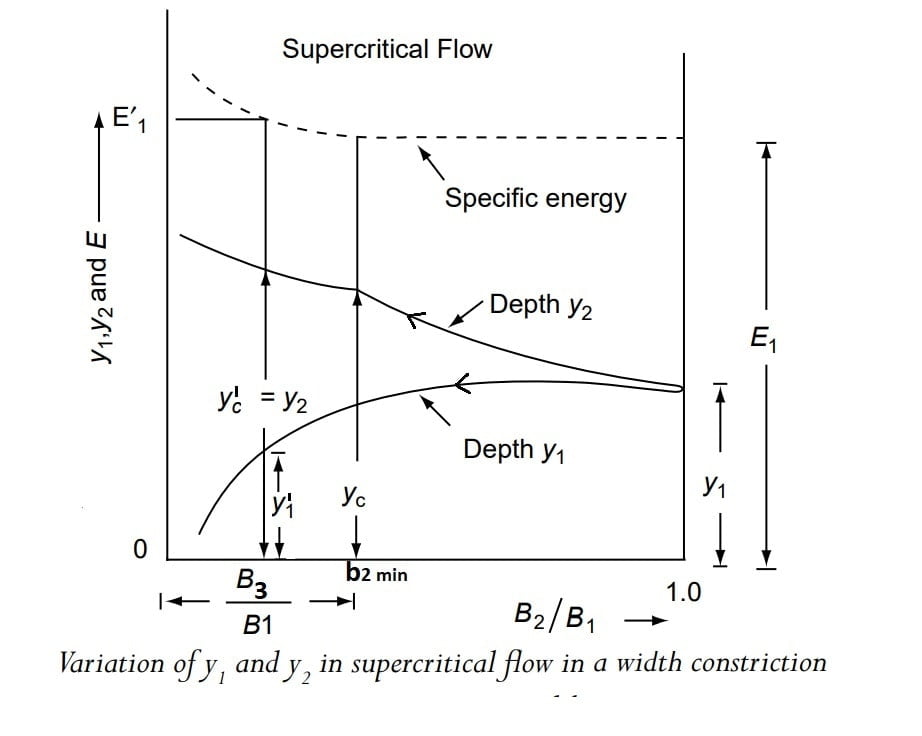
 2. Supercritical Flow
2. Supercritical Flow