Introduction
Many surveys have the primary goal of finding the area of the surveyed tract and the amount of earthwork.
Measurement of Area
- The method adopted for measurement of area and volume depends upon
1. Accuracy required
2. Shape/ Geometry of track. - Measurement can be done by either
1. By field measurement
2. By plan measurement - If the plan is enclosed by a straight line, it can be divided into geometrical figures, like: triangle, rectangle, square etc. The area of these figures can be determined by using standard formulas.
- But if the boundaries are irregular, then approximate methods are being used.
Note: Planimeter meter is used to determine areas of irregular shape.
Computation of Area of Geometrical Figures
1.Rectangle | Area= length(L) × width(b) |
2.Square | Area= length(L) × width(b) |
3.Triangle | Area= half of the base(b) × perpendicular height(h) |
4.Circle | Area = Π × (Radius)2 |
5.Parallelogram | Area= base × perpendicular height |
6.Trapezoid | Area= half of the sum of parallel sides × perpendicular height |
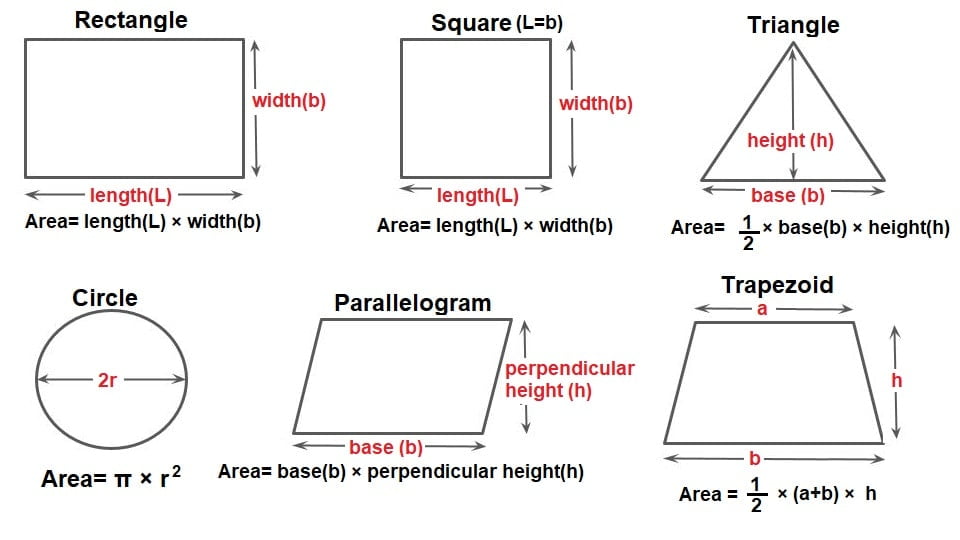
7.Trapezium
Area (ABCD) = Area(ABC) + Area(ACD)
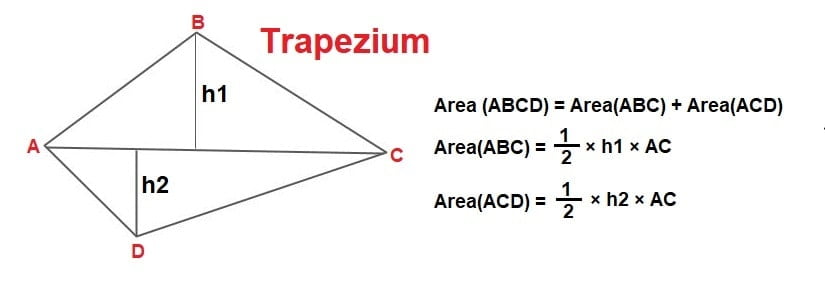
8.Oblique Triangle
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)
where a, b, care the sides.
\(s=\frac{a+b+c}{2}\)
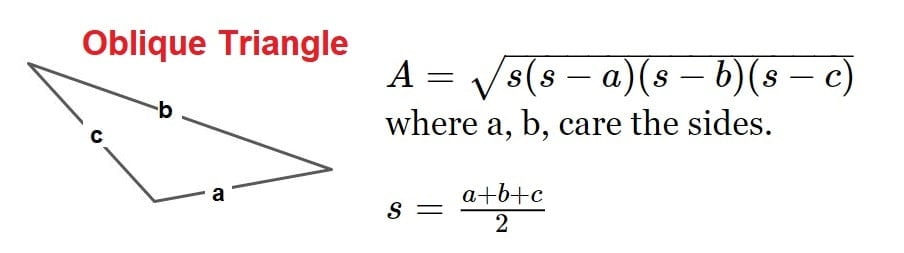
9.Area of a Segment
Area of segment (ACB) = Area of sector (ACBO) – Area of triangle (AOB)
| \(A=\frac{\Pi R^{2}}{360^{\circ}}\times \alpha -\frac{1}{2}\times 2Rsin\frac{\alpha }{2}\times Rcos\frac{\alpha }{2}\) |
| \(A=R^{2}\left ( \frac{\Pi \alpha }{360^{\circ}} -\frac{sin}{2}\right )\) |
\(A=R^{2}\left ( \frac{\Pi \alpha }{360^{\circ}} -\frac{sin}{2}\right )\)
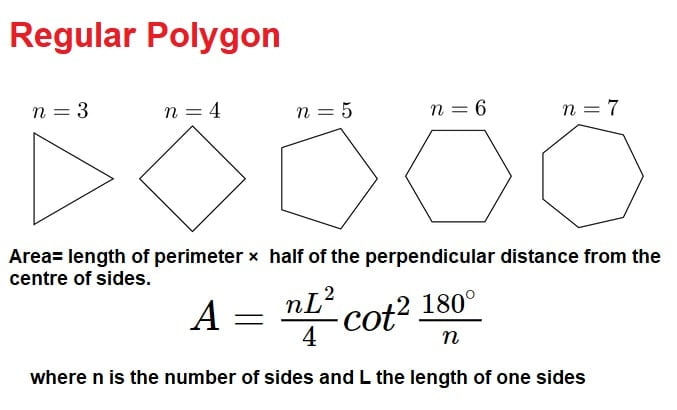
10.Regular Polygon
Area= length of perimeter × half of the perpendicular distance from the centre of sides.
| \(A=\frac{nL^{2}}{4}cot^{2}\frac{180^{\circ}}{n}\) |
where n is the number of sides and L the length of one sides
Computation of Area of Irregular Shape
1.Mid Ordinate Rule
If offsets h1, h2, …., hn-1. are measured at the mid point of each division.
Area = average ordinate × length of base.
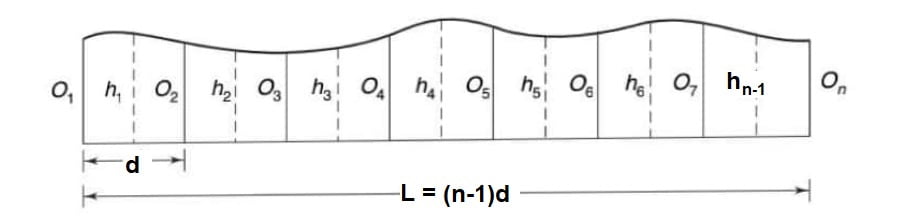
\(A=\frac{h_1+h_2+….+h_{n-1}}{n-1}L\).
∴L=(n-1)d
| \(A=\frac{h_1+h_2+….+h_{n-1}}{n-1}(n-1)d\) |
| \(A=(h_1+h_2+…+h_{n-1})d\) |
where
n-1 = number of division
d = distance between the two perpendicular offsets.
L = length of base line {L=(n-1)d}
2.Average Offset Rule
If offsets O1, O2, …., On. are measured at the mid point of each division and spaced apart at equal distance d.

Area = average of all ordinate × length of base.
\(A=\frac{O_1+O_2+….+O_n}{n}L\)
| \(A=\frac{O_1+O_2+….+O_n}{n}(n-1)d\) |
\(A=\frac{(n-1)d}{n}\Sigma O_i\)
3.Trapezoidal Rule
The accuracy of this method is more than mid-ordinate and average ordinate method.
Area of first trapezoid \(=\frac{O_1+O_2}{2}d\).
Area of second trapezoid \(=\frac{O_2+O_3}{2}d\).
Area of last trapezoid \(=\frac{O_{n-1}+O_n}{2}d\).
Total area of trapezoid
| \(A=\frac{1}{2}(O_1+O_2)d+\frac{1}{2}(O_2+O_3)d+….+\frac{1}{2}(O_{n-1}+O_n)d\) |
| \(A=\frac{1}{2}d[O_1+2O_2+2O_3+2O_{n-1}+O_n]\) |
| \(A=d[\frac{O_1+O_N}{2}+O_2+O_3+…O_{n-1}]\) |
4.Simpson’s One Third Rule
- If the boundaries of irregular tract are curved then Simpson method is preferred over the trapezoidal rule to calculate the area of given track.
- In this the curved boundary is considered to be a parabolic arch.

| \(A=\frac{d}{3}[(O_1+O_n)+4(O_2+O_4+…+O_{n-1})+2(O_3+O_5+…+O_{n-2})]\) |
Note
- To apply Simpson’s rule offsets should be odd in number.
- To work with even no of offsets Simpson’s should be apply upto last offsets and remaining area should be calculated using trapezoidal rule.
Measurement Of Volume
The computation of the volume of different quantities is required for planning & designing of various engineering work .
- Earthwork for highway, railway, retaining walls.
- Volume for reservoir capacity
- Concreting work
- Storage requirement
Computation of Volume of Irregular Shape
1.Trapezoidal Rule / End Area Method
This method is also called as end are method.
| \(V=d[\frac{A_1+A_n}{2}+A_2+A_3+…A_{n-1}]\) |
2.Prismoidal / Simpson’s Rule
| \(V=\frac{d}{3}[(A_1+A_n)+4(A_2+A_4+…+A_{n-1})+2(A_3+A_5+…+A_{n-2})]\) |
Note
- This formula usually gives less volume than trapezoidal formula.
- This formula is not suitable for rock excavation and concrete work.
- To apply Simpson’s rule offsets should be odd in number.
- To work with even no of offsets Simpson’s should be apply upto last offsets and remaining volume should be calculated using trapezoidal rule.
Amazing detailed elaborative concepts. It is only examples you have not included