Introduction of Unsteady Flow
Unsteady flow also called ‘Transient Flow’, occurs in the open channel when the discharge or depth or both vary with respect to time at a given section.
Unsteady flow can be due to natural cause, planned action, or accidental happenings.
Unsteady flows can be further classified, based on curvature
1. Gradually varied unsteady flow (GUVF), Example: Flood flow in a stream.
2. Rapidly varied unsteady flow (RUVF). Example: Formation and travel of surge due to sudden closure of a sluice gate.
Surges in Open Channel
⇒ Surge is an unsteady phenomenon that occurs under a situation like closure or opening of valves, gates, loading or unloading of turbines, start or stopping of pumps, failure of dams leading to flow of reservoir downstream, ETC.
⇒ Depending on the direction of movement of these waves, flow depth either may decrease or increase in the flow direction.
⇒ A surge producing an increase in flow depth is called a positive surge and the one which causes a decrease in flow depth is called a negative surge.
⇒ In other words if the wave is higher than the original steady flow depth, we call it a positive surge. In a negative surge, the situation is just the opposite.
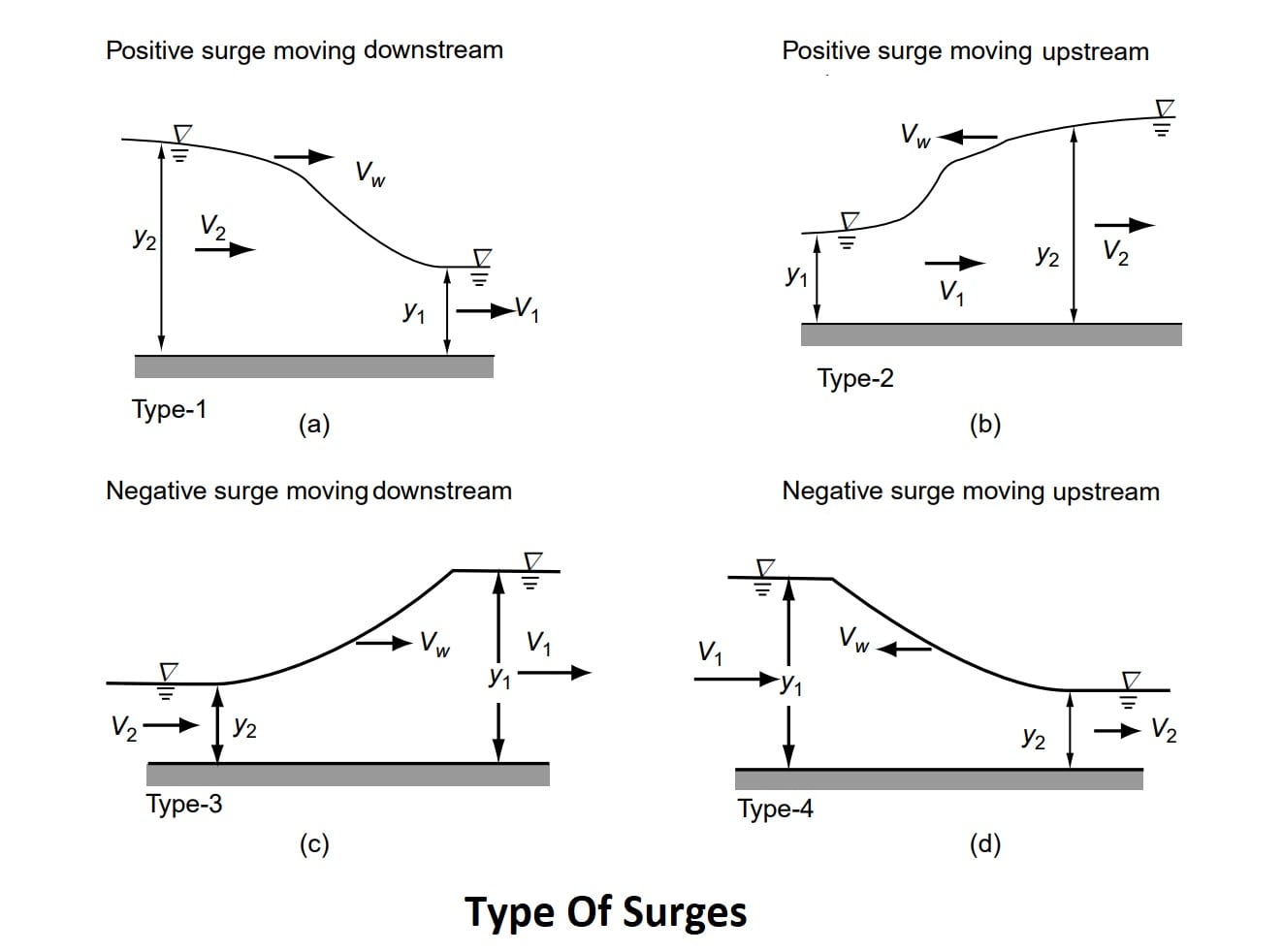
⇒ A surge can travel either upstream or downstream direction, thus giving rise to four basic types.
Type Of Surges
Where vw = Velocity of wave or surge
(A) Positive Surge Moving Downstream:
In figure -a (Type -1). At section 1, the depth of flow is y1 at a time ‘t’. when wave (surge) passes section 1 (time = t+Δt), the depth of flow is increased that wise surge is positive, and the surge moves in the downward direction so it is called a “Positive Surge Moving Downstream”.
(B) Positive Surge Moving Upstream:
In figure -b (Type -2). At section 1, the depth of flow is y1 at a time ‘t’. when wave (surge) passes section 1 (time = t+Δt), the depth of flow is increased that wise surge is positive, and the surge moves in the upward direction so it is called a “Positive Surge Moving Upstream”.
(C) Negative Surge Moving Downstream:
In figure -c (Type -3). At section 1, the depth of flow is y1 at a time ‘t’. when wave (surge) pass section 1 (time = t+Δt), the depth of flow is decreased that wise surge is negative, and the surge moves in the downward direction so it is called a “Negative Surge Moving Downstream”.
(D) Negative Surge Moving Upstream:
In figure -D (Type -4). At section 1, the depth of flow is y1 at a time ‘t’. when wave (surge) passes section 1 (time = t+Δt), the depth of flow is decreased that wise surge is negative, and the surge moves in the upward direction so it is called a “Negative Surge Moving Upstream”.
Note:
- How to decide surge increase or decrease the depth.⇒ If y2>y1 ⇒ Positive Surge. y2 < y1 ⇒ Negative Surge. (In other words, we say that in fig (a). when the wave passed section 2 at a time ‘t’, the depth of flow at section 2 is y2 which increased due to the wave then the wave will pass section 1 at a time ‘t+Δt’ the depth of flow will increase.)
- Arrow of a wave for downstream flow (→) and for upstream flow(←).
- Section 1 will always be on the front side of the arrow. And section 2 will always be on the back side of the arrow.
- (y2 → y1) (y1 ← y2).
| Surge Type | Example |
| Positive surge moving downstream | Downstream to sluice gate when suddenly open. |
| Positive surge moving upstream | Upstream to sluice gate when suddenly closed. |
| Negative surge moving downstream | Downstream to sluice gate when suddenly closed. |
| Negative surge moving upstream | Upstream to sluice gate when suddenly open. |
Analysis of Surges
For the analysis of surges which is a rapid varied unsteady flow, an equivalent steady flow situation is formed by considering the flow with respect to the surge.
Case A- Positive Surge Moving Downstream Due to Sudden Open Sluice Gate
⇒ Consider a situation in which positive surge is formed & is moving in d/s direction.
⇒ Flow depth at section 1 and 2 are y1, and y2, with velocities being v1, and v2.
⇒ A wave of height Z (+ve surge) is moving downstream with velocity vw
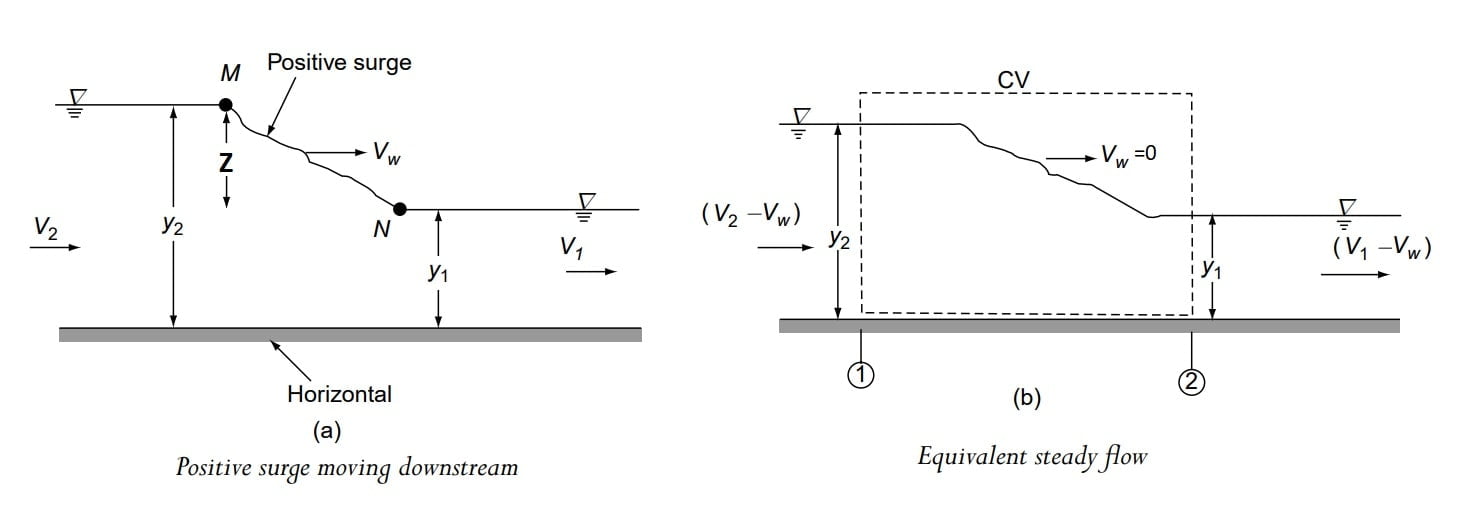
⇒ If a negative velocity equal to -vw is super imposed on the flow field, the wave will appear to have a stationary reference and flow field will convert to a steady flow.
Note: Superimposing a negative velocity of (-vw) can be considered to the observing the flow by taking surge as a reference frame.
Step-1 Apply continuity equation between section 1 and 2
A1 (v1-vw) = A2 (v2-vw)
Step-2 Application of Momentum Equation
Applying momentum equation between section 1 and 2 by neglecting fractional losses, and assuming hydrostatic pressure distribution at section 1 & 2.
P1 – P2 = M2 – M1
M1 & M2= momentum per unit time at section 1 & 2 respectively or momentum flux
momentum per unit time = m·v/t
m=ρ·V
∴ {density (ρ) = mass (m) / volume (V)}
V/t = Q, ∴{Discharge= Volume/time}
M1 = ρ·Q·v1 = ρ·A1(v1-vw)·(v1-vw)
M2=ρ·Q·v2 = ρ·A1(v1-vw)·(v2-vw)
P1 & P2= Pressure force acting at section 1 & 2 respectively
γ·A1·\(\bar{y_1}\) – γ·A2·\(\bar{y_2}\) = ρ·A1(v1-vw)[(v2-vw) – (v1-vw)]
The number of variable in the above two equation are five ( y1, y2, v1, v2, vw). Three variable are given remaining 2 are calculated by Continuity equation, Momentum Equation.
Case B- Positive Surge Moving Upstream Due to Sudden Closed Sluice Gate
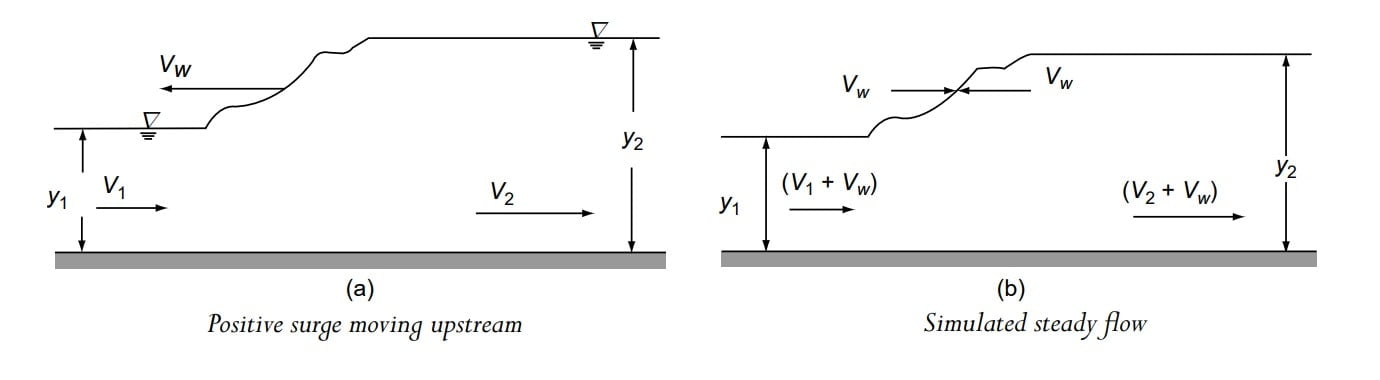
Step-1 Apply continuity equation between section 1 and 2
A1 (v1+vw) = A2 (v2+vw)
Step-2 Application of Momentum Equation
Applying momentum equation between section 1 and 2 by neglecting fractional losses, and assuming hydrostatic pressure distribution at section 1 & 2.
P1 – P2 = M2 – M1
M1 & M2= momentum per unit time at section 1 & 2 respectively or momentum flux
momentum per unit time = m·v/t
m=ρ·V
∴ {density (ρ) = mass (m) / volume (V)}
V/t = Q, ∴{Discharge= Volume/time}
M1 = ρ·Q·v1 = ρ·A1(v1-vw)·(v1-vw)
M2=ρ·Q·v2 = ρ·A1(v1-vw)·(v2-vw)
P1 & P2= Pressure force acting at section 1 & 2 respectively
γ·A1·\(\bar{y_1}\) – γ·A2·\(\bar{y_2}\) = ρ·A1(v1+vw)[(v2+vw) – (v1+vw)]
The number of variable in the above two equation are five ( y1, y2, v1, v2, vw). Three variable are given remaining 2 are calculated by Continuity equation, Momentum Equation.
Note:
Celerity
The velocity small disturbance surge / wave relative to the initial flow velocity in canal is called celerity.
For surge moving d/s, C = (vw–v1)
For surge moving u/s, C = (vw+v1)
The value of celerity in either of above two cases comes out to be same.
\(C= \sqrt{\frac{1}{2}\cdot g\cdot \frac{y_2}{y_1}\cdot (y_1+y_2)}\)
Here the height of surge = (y2–y1)
For a wave of small height (y2–y1) ≈ 0 or y2 = y1 = y
\(C= \sqrt{\frac{1}{2}\cdot g\cdot \frac{y_2}{y_1}\cdot (2y)}\).
\(C= \sqrt{gy}\).