Photogrammetry
Photogrammetry is the science of obtaining information about physical objects through process of recording, measuring and interpreting of photographs of the area.
In other words, ‘photogrammetry can be defined as the process of developing a map by combining different photographs of the earth’s surface.
Advantage & Disadvantage of Photogrammetry
| Advantage | Disadvantage |
| Covers large area | Complex system, highly trained human resource needed |
| Less time consuming/fast | Costly at the time of installation/initiation |
| Cheap/cost effective for large area and in a long run | Heavy and sophisticated equipment’s needed |
| Easy to interpret, understand | Lengthy administrative procedure for getting permission to fly |
| Can ‘reach’ inaccessible and restricted area | Weather dependent |
Types of Photogrammetry
There are two types of photogrammetry.
- Terrestrial Photogrammetry.
- Aerial Photogrammetry.
Terrestrial Photogrammetry (Horizontal Photograph)
- Terrestrial photogrammetry is the branch of the photogrammetry in which photographs are taken with a camera fixed on or near the ground.
- It is also called as Ground Photogrammetry.
- In terrestrial photogrammetry camera axis is horizontal.
- In terrestrial photogrammetry the instrument used is a photo-theodolite. (Photo-theodolite is nothing but a conventional camera fitted on a tripod with the camera axis horizontal and a theodolite.)
- Use of terrestrial photogrammetry is limited to the plotting of special features eg. vertical cliff, mountainous terrain etc.
- Similar to plane tabling, the plotting work is done in the field only.
Aerial Photogrammetry
- Aerial photogrammetry is the branch of photogrammetry in which photographs of the area are taken with a camera mounted on an aircraft.
- It is also called as Ground Photogrammetry.
- In aerial photogrammetry, the same camera is used but the camera axis is vertical.
- Use of aerial photograph is used for topographical surveys, forest and agricultural surveys, preliminary route surveys, i.e. highways, railways pipelines, etc.,
- In aerial photogrammetry, large area can be covered in less time, no detail is missed, can also be used for inaccessible areas.
Difference Between a Map and An Aerial Photograph
| Map | Aerial Photograph |
| It is an orthogonal projection. | It is a central projection, i.e., perspective projection. |
| Selected details are shown. | A vast number of details are available. |
| More clarity due to use of legends and other symbolic representations. | Less clarity due to no symbolic representations etc. |
| It has a constant scale. | Here the scale differs due to variation of elevations. |
Types of Photographs
Aerial photographs are classified into two types:
- Vertical Photograph
- Oblique Photograph
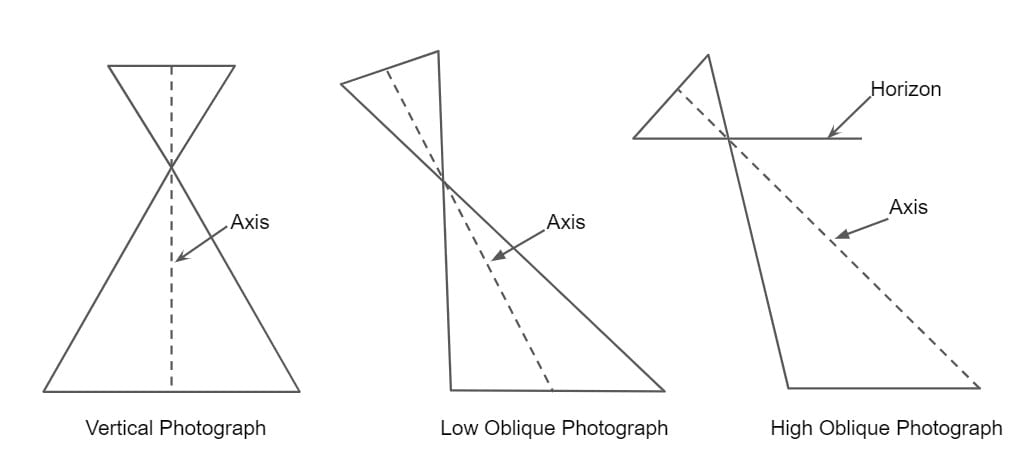
1. Vertical Photograph
- A vertical photograph is an Aerial photograph made with camera axis coinciding with the direction of gravity.
- In truly vertical photograph, the photo plane is parallel to the datum plane.
- Tilted Photograph: When the camera axis is tilted from vertical, the resulting photographs is known as tilted photograph. The tilt is generally less than 3°.
2. Oblique Photograph
- When the vertical axis of the camera is intentionally inclined to the vertical then the resultant photograph is known as oblique photograph.
- A high-oblique photograph is one that includes the horizon, whereas a low-oblique photograph does not include it.
Terminologies in Aerial Surveying
1.Scale of Photograph

Scale of a vertical photograph is define as the ratio of image distance to object distance. For vertical photographs taken over variable terrain, there are an infinite number 0f different scales. this is one the principle difference between a photograph and a map.
The scale of the flat terrain photograph,
S= \(\frac{\text{photo distance}}{\text{ground distance}}\) = \(\frac{ab}{AB}\)
from similar triangle ΔLab & ΔLAB
\(\frac{ab}{AB}\) = \(\frac{f}{H’}\) = \(\frac{f}{H-h}\)
S = \(\frac{f}{H-h}\)
The scale of the variable terrain photograph,
S= \(\frac{ab}{AB}\) = \(\frac{cd}{CD}\)
from similar triangle ΔOab & ΔOAB
\(\frac{ab}{AB}\) = \(\frac{f}{H-h_1}\) = \(\frac{f}{H-h}\)
from similar triangle ΔOcd & ΔOCD
\(\frac{cd}{CD}\) = \(\frac{f}{H-h_2}\) = \(\frac{f}{H-h}\)
In general, the scale S of a photograph for any ground elevation is
S= \(\frac{f}{H-h}\)
Where
H= altitude of the aircraft above mean sea level,
h= elevation of the ground above mean sea level
f= focal length of the camera.
2.Datum Scale of Photograph
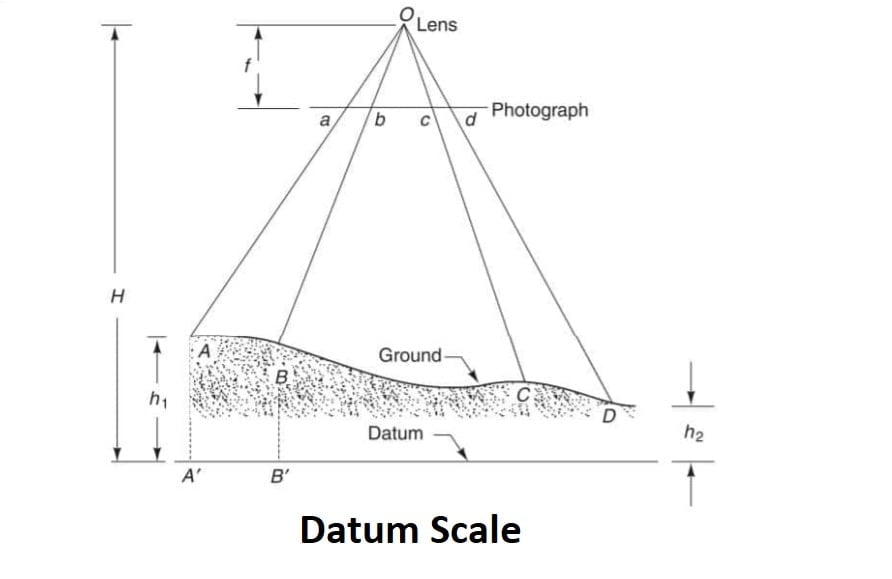
The datum scale is the scale effective over the entire photograph when all the ground points were projected vertically downwards on the datum.
Sd= \(\frac{f}{H}\)
3.Average Scale of Photograph

The average scale is the scale of vertical photograph, that would be effective over the entire photograph if all the ground points were projected vertically downward or upward on the plane of the average elevation of the ground before being photographed.
Savg= \(\frac{f}{H-h_{avg}}\)
4.Flying Height
The elevation of camera lens above datum is called as flying height. Generally mean sea level (MSL) is taken as the datum.
we know that scale of photograph,
S= \(\frac{f}{H-h}\)
so
(H-h)= \(\frac{f}{S}\)
where
H-h= flying height above ground
f= focal length of camera
S= scale of photographs
This method can give best result only when the ground is level or elevation of two point are same.
5.Crab
Crab of a photograph is the angle between the flight line of the aircraft and the edges of the photograph in the direction of flight.
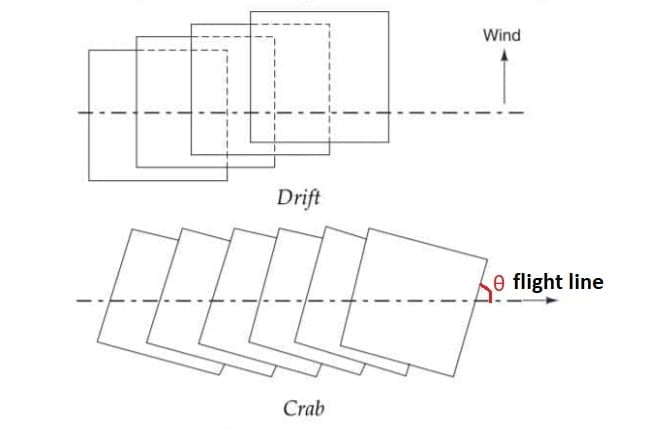
6.Drift
Drift is the lateral shifting of the the photograph. The photograph does not stay on the predetermined flight line due to winds. If the aircraft is set on its course without considering the wind velocity, drift will occur.
Ground Co-Ordinates & Length of a Line From a vertical Photograph
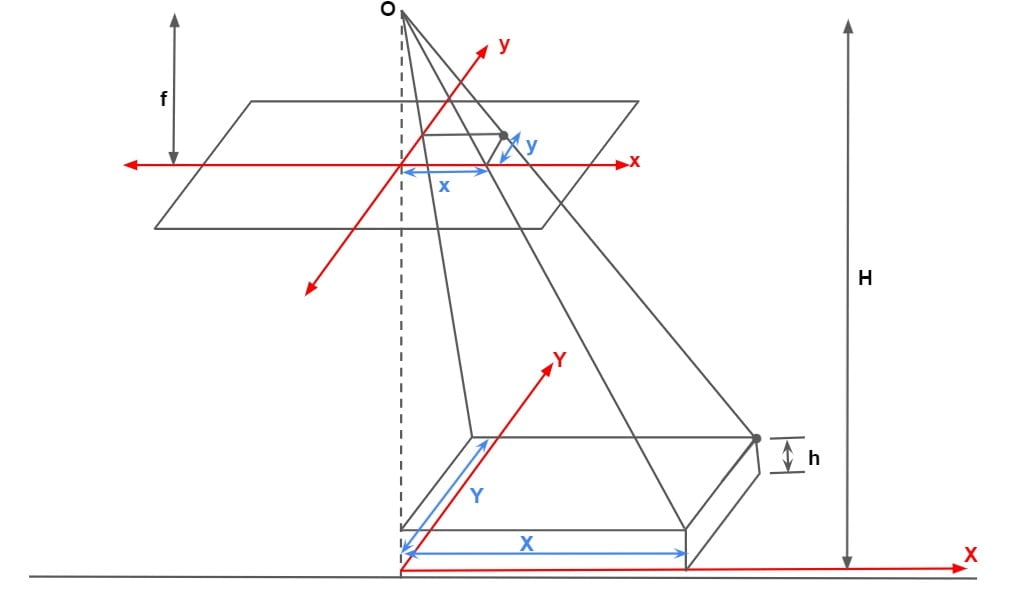
The lengths of the lines can be determined from the photographic coordinates (x, y) and ground coordinates (X, Y).
\(\frac{x}{X}=\frac{f}{H-h}\)and
\(\frac{y}{Y}=\frac{f}{H-h}\)The ground coordinates are referred to the plumb point as the origin, the coordinate axes being parallel to the geometrical axes of the photograph, the X-axis being in the direction of the line of the flight.
Let it be required to determine the length of a line AB on the ground from the coordinates of the end points a and b photographed using the principal point as the origin.
\(X_A=\frac{H-h}{f}x_a\), \(Y_A=\frac{H-h}{f}y_a\)
and
\(X_B=\frac{H-h}{f}x_b\), \(Y_B=\frac{H-h}{f}y_b\)
the horizontal distance
AB= \(\sqrt{(X_A-X_B)^{2}+(Y_A-Y_B)^{2}}\)
Relief Displacement

Relief is the elevation of object above or below the datum. Displacement of any point on photograph from its true orthographic position due to height of object is called relief displacement.
from ΔOKa & ΔOKA
\(\frac{r}{R}=\frac{f}{H-h}\).
\(r=\frac{rf}{H-h}\).
from ΔOkao & ΔOKoAo
\(\frac{r_o}{R}=\frac{f}{H}\).
\(r_o=\frac{Rf}{H}\).
Relief displacement d= r-ro
\(d=\frac{Rf}{H-h}-\frac{Rf}{H}\).
\(d=Rf*\frac{H-H+h}{(H-h)H}\).
\(d=\frac{Rf*h}{(H-h)H}\).
\(d=\frac{h*r}{H}\)
If tower is standing on ground of elevation havg
then
\(d=\frac{h*r}{H-h_{avg}}\)
Area Covered By One Photograph
Area Covered By One Photograph= (Length × Scale)(Width × Scale)
Number of Photograph Required to Cover an Area
1.When No overlap is Present
\(N=\frac{\text{Total Area on Ground}}{\text{Area Covered By One Photograph}}\)
2.When overlap is Present (Longitudinal & Side)
There are 2 case.
- When total ground area is given.
- When length & width are given of total ground
(I). When Total Ground Area (A) is given
Let
PL=Longitudinal overlap = 0.6 (default)
PB= Side overlap = 0.3 (default)
L= Length of ground being surveyed (Respectively each photograph) ≠Total length
B = Width of ground being surveyed (Respectively each photograph) ≠Total width
l = Length of photograph in the flight direction
b = Width of photograph in the direction normal to flight direction
S = Scale of the photograph = \(\frac{\text{photo distance}}{\text{ground distance}}\)
Thus,
L = (1 – PL)l/S
B = (1 – PB )b/S
Thus ground area covered by each photograph is,
a= LB= (1-PL)(1-PB)(l/S)(b/S)
a = lb(1 – PL) (1 – PB)/S2
A= Total Area ≠ LB
Number of photographs required to cover the area, N= A/a
(II). When Length & Width are given of total Ground
Let
L’ = total length of ground
B’ = total width of ground
PL=Longitudinal overlap = 0.6 (default)
PB= Side overlap = 0.3 (default)
l = Length of photograph in the flight direction
b = Width of photograph in the direction normal to flight direction
S = Scale of the photograph = \(\frac{\text{photo distance}}{\text{ground distance}}\)
Thus,
Total No of photograph required N=N1×N2
N= \(\left [ \frac{L’}{(1-P_L)\frac{l}{S}}+1 \right ]\)× \(\left [ \frac{B’}{(1-P_B)\frac{b}{S}}+1 \right ]\)
Where
N₁ = No. of photographs in each strip
N₂= No. of strips
Exposure Interval
If the ground speed of the aircraft is V (km/h) and the ground distance covered between exposures along the flight line is L (km), the time interval between exposures, in seconds, is given
\(T=\frac{3600×L}{V}\)
Air Base
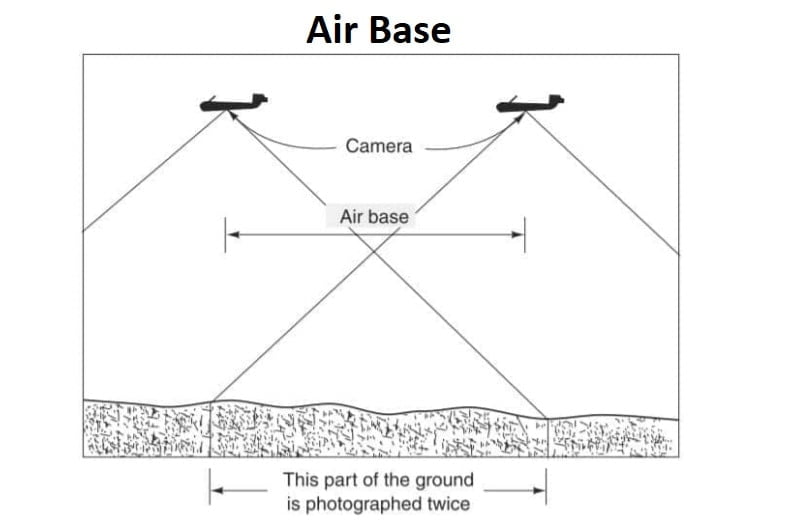
The distance covered by an aircraft between any two successive exposures is known as the air base and is shown.
More studying materials for photogrammetry ,notes, summarizes and questions
please this has been so helpful. provide some more notes
please this has been so helpful. provide some more notes