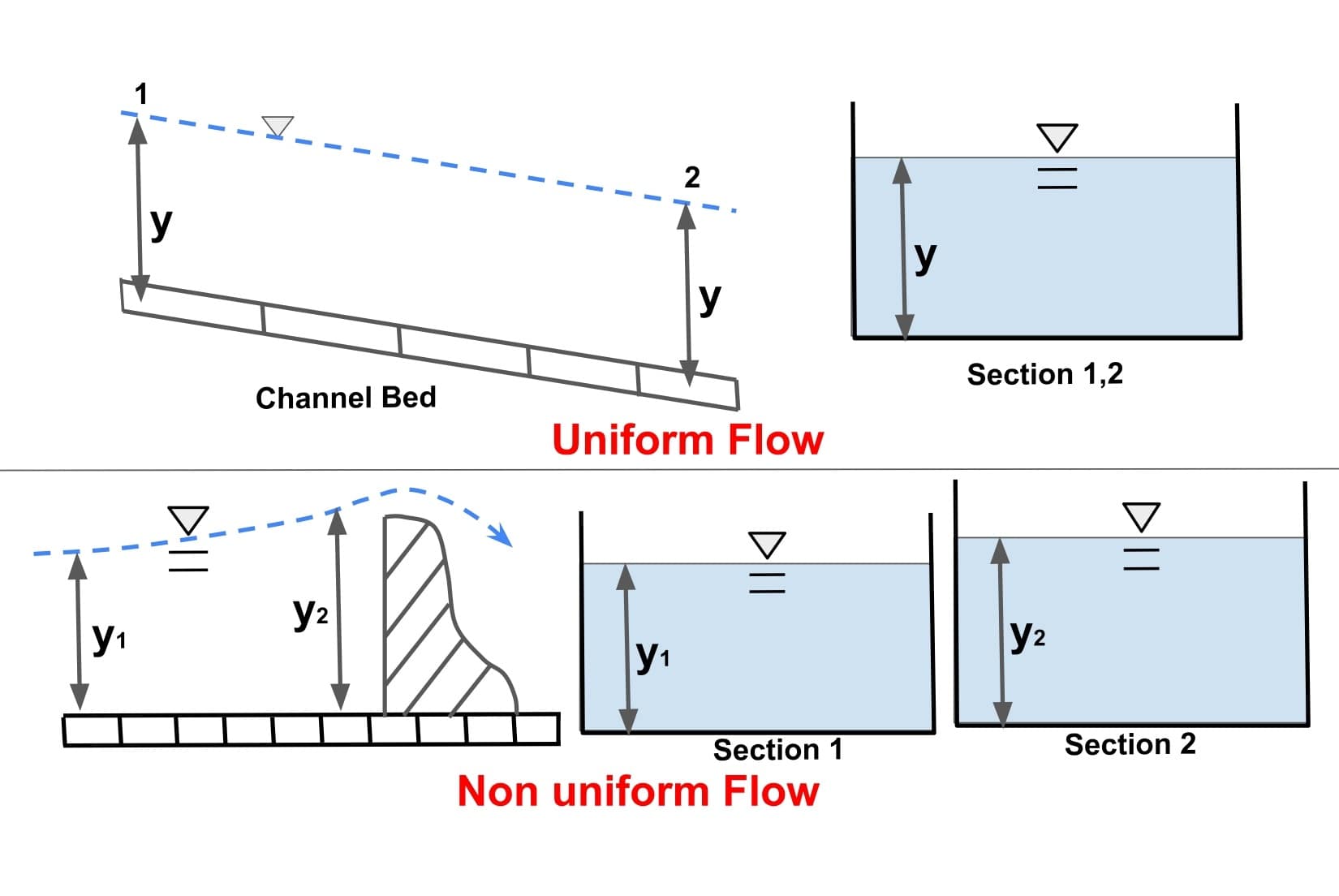
Uniform Flow
⇒ A flow in open channel is said to be uniform flow if its properties remains constant with respect to space. i.e depth of flow, area of flow, rate of flow, velocity of flow do not change along the channel.
\(\frac{dy}{dx}=0\).
\(\frac{dv}{dx}=0\).
\(\frac{dQ}{dx}=0\).
⇒ The constant depth of flow is uniform flow is called “Normal Depth”.
⇒ As the depth of flow & velocity at every section are constant therefore channel bed slope, water surface slope, energy lone slope will be same. And the total energy line , water surface and the channel bottom are all parallel in a uniform flow.
⇒ A prismatic channel charring certain discharge with constant velocity is an example of uniform flow.
⇒ In uniform flow frictional resistance acting between fluid and channel boundary are balance by the gravity force.
⇒ In uniform flow velocity of flow does not change along the length of channel, acceleration is zero hence the sum of all the component of all external force in direction of flow must be zero.
Analysis of Uniform Flow
Chezy Equation
By definition there is no acceleration in uniform flow. By applying the momentum equation to a control volume encompassing Sections 1 and 2, distance L apart, as shown in Fig.
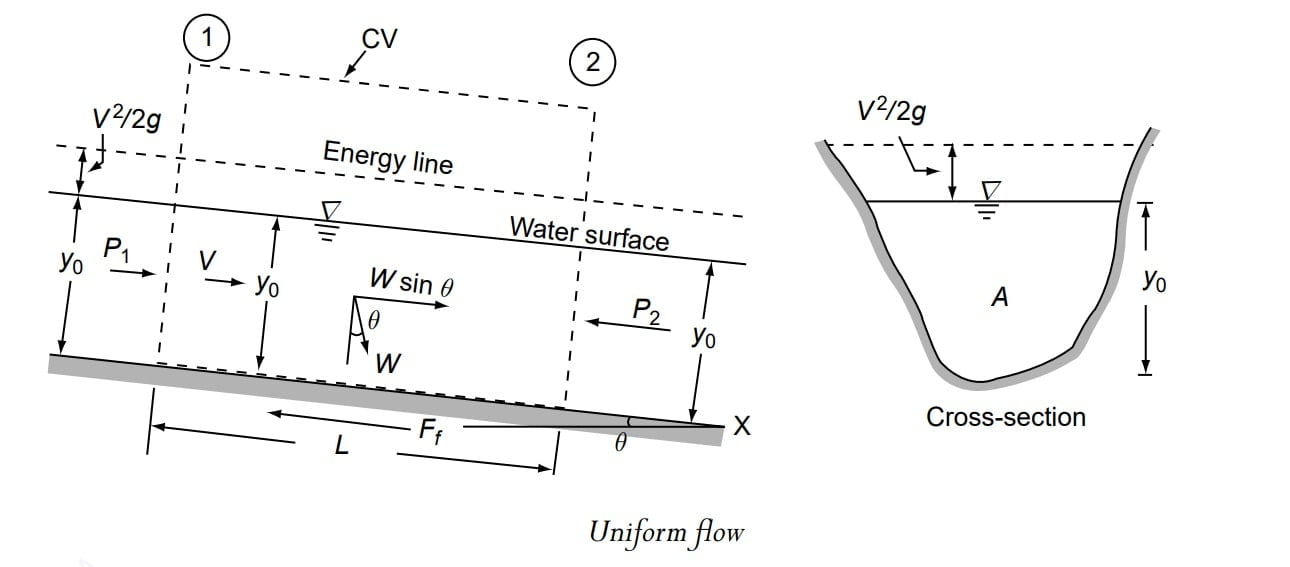
P1 − W sin θ − Ff− P2= M2− M1 (momentum equation)
where
P1 & P2 = pressure forces at sections 1 and 2 respectively
M1 & M2 = momentum fluxes at sections 1 and 2 respectively
W = weight to fluid in the control volume
Ff = shear force at the boundary.
Since the flow is uniform,
P1 = P2 ,
& M1 = M2
so
P1 − W sinθ − Ff− P2= M2− M1
W sin θ = Ff
Also, W = γ AL (A=area, L = length) If θ is small, θ ≈ sinθ ≈ tanθ where tanθ= slope of channel bed ‘So‘. | Ff = τ0 PL (τ0 = average shear stress acting over channel boundary) (τ0 = average shear stress on the wetted perimeter P of length L) |
γ·A·L·So = τ0 PL
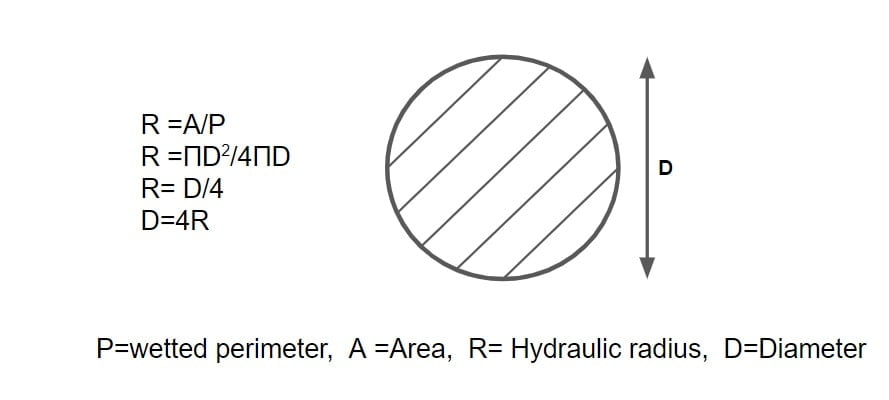
τ0 = γ·(A/P)·So
τ0 = γ·R·So …..(1)
R= hydraulic radius =(A/P)
γ = unit weight of the fluid
From various experiments on shear stress on wetted area under uniform flow condition, it is observed to be proportion to dynamic pressure \(\frac{\rho \cdot v^{2}}{2}\) & independent of viscosity.
\(\tau_o \propto \frac{\rho \cdot v^{2}}{2}\)
\(\tau_o = k \frac{\rho \cdot v^{2}}{2}\) …..(2)
k = constant dependent on the roughness of the channel
from equation 1 & 2
\(k \frac{\rho \cdot v^{2}}{2}\) = γ·R·So
\(v=\sqrt{\frac{2\gamma }{k\rho }}\cdot \sqrt{RS_o}\).
\(v=c\sqrt{RS_o}\)
here constant c is chezy’s constant, c = \(\sqrt{\frac{2\gamma }{k\rho }}\). & the above equation is termed as chezy’s equation.
\(v=c\sqrt{RS_o}\)
where
v= Average velocity
R= Hydraulic radius of the channel section
So = Bed slope of the channel
C = Constant, depends on the nature of flow and nature of surface.
Note:
- Chezy’s coefficient is not dimensionless & it has the dimensions [L½T-1]
- In uniform flow, we know that slope of bed(SO) = slope of energy line(Sf) =S.
Derivation From Darcy’s Weisbach Equation
the Darcy Weisbach equation is
\(h_f= f\frac{L\cdot V^{2}}{D\cdot 2g}\)
where
hf = head loss due to friction in a pipe of diameter D and length L
f= Darcy Weisbach friction factor.
\(h_f= f\frac{L\cdot V^{2}}{8g\cdot R}\)
\(v=\sqrt{\frac{8g}{f}}\sqrt{R\frac{h_f}{L}}\)
This equation in applied for analysis of pipe flow.
\(v=c\sqrt{R\frac{h_f}{L}}\)
\(v=c\sqrt{R\cdot S_o}\)
here, c=\(\sqrt{\frac{8g}{f}}\)
Manning’s Equation
As per Manning’s average velocity of flow in open channel undergoing uniform flow is given by
\(v= \frac{1}{N}\cdot R^{2/3}\cdot S_o^{1/2}\).
where
R= Hydraulic radius of the channel section
So = Bed slope of the channel
N= roughness coefficient that depends upon nature of boundary surface. It value generally varies in the range of 0.011-0.05.
Relationship Between Chezy’s Constant & Friction Factor
we know that chezy’s equation.
\(v=c\sqrt{RS}\) …(1)
and Manning’s Equation
\(v= \frac{1}{N}\cdot R^{2/3}\cdot S_o^{1/2}\) …(2)
compare both 1 & 2
\(c= \frac{1}{N}\cdot R^{1/6}\)
also we know that
c=\(\sqrt{\frac{8g}{f}}\)
\(\frac{1}{N}\cdot R^{1/6}= \sqrt{\frac{8g}{f}}\)
\(f=8g\cdot \frac{N^{2}}{R^{1/3}}\)
Momentum Equation of Uniform Flow
By applying the momentum equation to a control volume encompassing Sections 1 and 2, distance L apart, as shown in Fig.

P1 − W sin θ − Ff− P2= M2− M1
where
P1 & P2 = pressure forces at sections 1 and 2 respectively
M1 & M2 = momentum fluxes at sections 1 and 2 respectively
W = weight to fluid in the control volume
Ff = shear force at the boundary.
Since the flow is uniform,
P1 = P2 ,
& M1 = M2
So
P1 − W sinθ − Ff− P2= M2− M1
W sinθ = Ff
Thus energy derived from flow due to gravity is lost in over coming friction.
Most Economical Or Most Efficient Section of Channel
⇒ A section is said to be economical when its construction cost is minimum for a given discharge.
⇒ A section is said to be most efficient, if for a given cross sectional area, the discharge carrying capacity is maximum.
⇒ As we all know, the cost of lining is the greatest component of overall construction cost in a channel section, and if the perimeter is kept to a minimum, hence it will be most economical section.
⇒ For a maximum discharge for a given area A, perimeter should be minimum. As we can observe that Q is inversely proportional to P2/3.
From Manning’s Equations
\(Q=\frac{1}{n}AR^{2/3}S^{1/2}\).
\(Q=\frac{1}{n}A(\frac{A}{P})^{2/3}S^{1/2}\).
\(Q=\frac{1}{n}\frac{A^{5/3}}{P^{2/3}}S^{2/3}\).
\(Q=\frac{1}{n}\frac{A^{5/3}}{P^{2/3}}S^{2/3}\).
\(Q\propto \frac{1}{P^{2/3}}\).
⇒ Also if perimeter is minimum, Resistance offered by the perimeter will be minimum hence discharge will be maximum.
⇒ Therefore for most economical and most efficient channel section perimeter should be minimum.
Relationship Between Various Element To From An Efficient Channel Section
- Most Efficient Rectangular Section
- Most Efficient Triangular Section
- Most Efficient Trapezoidal Section
1. Most Efficient Rectangular Section
For a rectangular channel,

A = By
and
P = B + 2y.
For the best hydraulic section, we want to determine the ratio of B and y such that P is minimum for constant A. Now, P can be written in terms of A and y as
\(P=\frac{A}{y}+2y\).
Differentiating this expression for P with respect to y and then equating the resulting expression to zero, we obtain
\(\frac{\mathrm{d} P}{\mathrm{d} y}=\frac{-A}{y^{2}}+2=0\).
\(\frac{A}{y^{2}}=2\).
But A = By. Therefore
\(\frac{By}{y^{2}}=2\).
\(y=\frac{B}{2}\).
or
B= 2y
\(R=\frac{A}{P}=\frac{By}{B+2y}\).
\(R=\frac{By}{B+B}\).
\(R=\frac{By}{2B}\).
\(R=\frac{y}{2}\).
⇒ Thus, a rectangular cross section is the most efficient when the flow depth is one-half the channel width.
Remember: For most economical rectangular channel.
- A=2y2
- B=2y=T
- P=4y
- R= y/2
- D=A/T=y
where,
A= Wetted Area or Area of flow,
B= width,
P= Wetted Perimeter,
R= Hydraulic Radius,
y= Depth of Flow,
D=Hydraulic Depth.
2. Most Efficient Triangular Section
Consider a triangular section having depth of flow y and varying side slope 1:m.
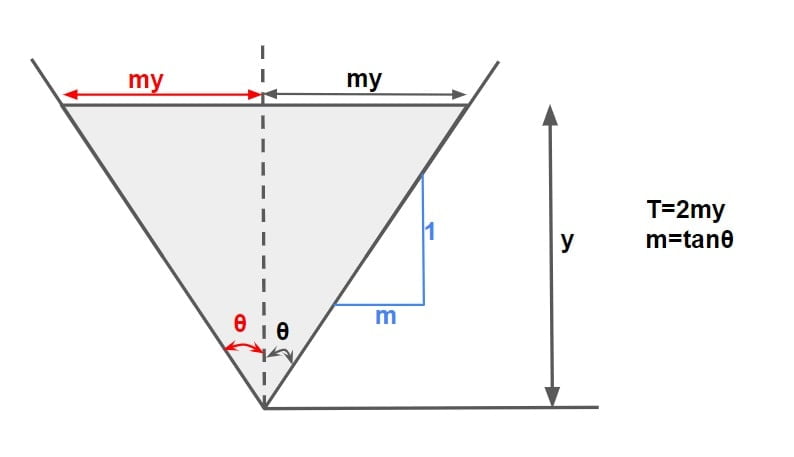
\(A=\frac{1}{2}\times 2my\times y\).
A=my2
A=tanθ·y2
P = 2y·secθ
Taking the square of both sides, this equation becomes
P2 = 4y2·sec2θ
P2 = 4y2(1+tan2θ)
we know that A=tanθ·y2
y2 =A·cotθ
P2 = 4·A·cotθ(1+tan2θ)
P2 = 4·A·(cotθ+tanθ)
Note: In the equation of P, A is constant. Only θ is varying.
Differentiating above equation with respect to θ.
\(2P\frac{\mathrm{d} P}{\mathrm{d} \theta }=4A(-cosec^{2}\theta +sec^{2}\theta )\).
\(\frac{\mathrm{d} P}{\mathrm{d} \theta }=\frac{4A(-cosec^{2}\theta +sec^{2}\theta )}{2P}\).
For given area ‘A’, ‘P’ is minimum when \(\frac{\mathrm{d} P}{\mathrm{d} \theta }=0\).
\(\frac{4A(-cosec^{2}\theta +sec^{2}\theta )}{2P}=0\).
\(4A(-cosec^{2}\theta +sec^{2}\theta )=0\).
cosec2θ= sec2θ
tan2θ= 1
θ=45°
so for most economical triangular channel θ=45°
Remember: For most economical triangular channel.
- A=y2
- \(P=2\sqrt{2}y\).
- T=2y
- \(R=\frac{y}{2\sqrt{2}}\).
- D = \(\frac{y}{2}\)
1.
we calculate that A=tanθ·y2
for most economical triangular channel θ=45°
A=tan45°·y2 (tan45°=1)
A=y2
2.
we calculate that P= 2y·secθ
for most economical triangular channel θ=45°
sec45°= \(\sqrt{2}\).
\(P=2\sqrt{2}y\).
3.
we calculate that T=2my
m=tanθ
for most economical triangular channel θ=45°
tan45°=1
T=2y
4.
\(R=\frac{A}{P}=\frac{y^{2}}{2\sqrt{2}y}\).
\(R=\frac{y}{2\sqrt{2}}\).
5.
D = \(\frac{A}{T}\).
D = \(\frac{y^{2}}{2y}\).
D = \(\frac{y}{2}\)
3. Most Efficient Trapezoidal Section
Case I: When side slope is fixed
Consider a channel section of bottom width =B, Depth of flow = y, side slope = 1:m (V:H)
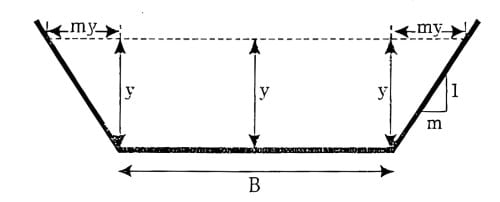
There are 3 variables y, B, m but m is fixed, the number of variable left out are y & B.
Area, \(A=\frac{1}{2}(B+T)y\).
Top width of flow, T= B+2my
\(A=\frac{1}{2}(B+B+2my)y\).
\(A=\frac{1}{2}(2B+2my)y\).
A= (B+my)y
P= B+ 2×length of side slope
P= B+ 2×length of side slope
side length = \(\sqrt{y^{2}+(my)^{2}}=y\sqrt{m^{2}+1}\)
\(P =B+2y\sqrt{m^{2}+1}\).
substituting, \(B=\frac{A}{y}-my\).
\(P =\frac{A}{y}-my+2y\sqrt{m^{2}+1}\).
In the equation of P, A & m are constant. only y is varying.
we know that for most efficient channel section of a given Area A, perimeter should be minimum.
\(\frac{\mathrm{d} P}{\mathrm{d} y}=0\).
\(\frac{\mathrm{d} P}{\mathrm{d} y}=\frac{-A}{y^{2}}-m+2\sqrt{m^{2}+1}\).
\(0=\frac{-A}{y^{2}}-m+2\sqrt{m^{2}+1}\).
\(\frac{A}{y^{2}}+m=2\sqrt{m^{2}+1}\).
Multiplying ‘y’ on both sides
\(\frac{A}{y}+my=2y\sqrt{m^{2}+1}\).
substituting \(\frac{A}{y}=B+my\).
\(B+my+my=2y\sqrt{m^{2}+1}\).
\(B+2my=2y\sqrt{m^{2}+1}\).
substituting, B+2my=T
\(T=2y\sqrt{m^{2}+1}\).
\(\frac{T}{2}=y\sqrt{m^{2}+1}\).
we know that, \(y\sqrt{m^{2}+1}\)= length of side slope.
\(\frac{T}{2}\)= Length of side slope
For most efficient trapezoidal channel section with fixed side slope half of top width should be equal to length of side slope.
For hydraulic radius, R = A/P
\(R=\frac{(B+my)y}{B+2y\sqrt{m^{2}+1}}\).
\(R=\frac{(B+my)y}{B+T}\).
\(R=\frac{(B+my)y}{B+B+2my}\).
\(R=\frac{(B+my)y}{2B+2my}\).
\(R=\frac{(B+my)y}{2(B+my)}\).
\(R=\frac{y}{2}\).
For most efficient trapezoidal channel section with fixed side slope, Hydraulic radius R should be equal to half of depth of flow.
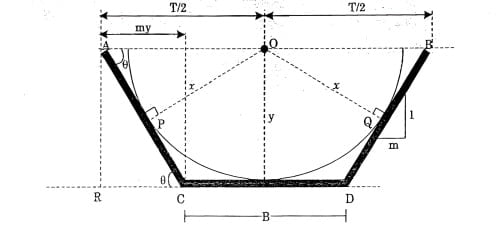
In Δ AOP,
\(sin\theta =\frac{OP}{AO}=\frac{x}{T/2}\).
In Δ ACR,
\(sin\theta =\frac{AR}{AC}=\frac{y}{y\sqrt{1+m^{2}}}\).
By comparing both the above equation
\(\frac{OP}{AO}=\frac{x}{T/2}=\frac{AR}{AC}=\frac{y}{y\sqrt{1+m^{2}}}\).
\(\frac{OP}{AO}=\frac{x}{y\sqrt{1+m^{2}}}=\frac{AR}{AC}=\frac{y}{y\sqrt{1+m^{2}}}\).
x=y
For most efficient trapezoidal channel section with fixed side slope, a circle of radius y shall be inscribed in the trapezoidal section.
For most efficient trapezoidal channel section with fixed side slope having depth of flow=y and fixed side slope 1:m all the condition should be satisfied.
- \(\frac{T}{2}\)= Length of side slope
- \(R=\frac{y}{2}\).
- (x=y) For most efficient trapezoidal channel section, a circle of radius y shall be inscribed in the trapezoidal section.
Case II: When side slope is varied.
Consider a channel section of bottom width =B, Depth of flow = y, varying side slope = 1:m (V:H)
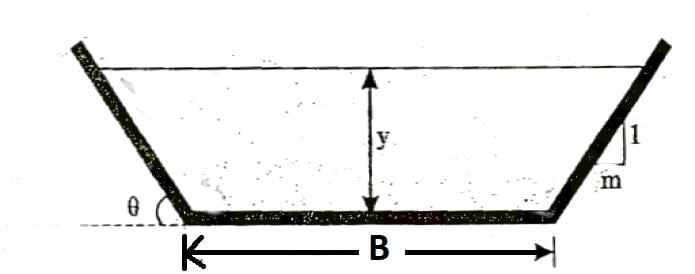
Area, \(A=\frac{1}{2}(B+T)y\).
Top width of flow, T= B+2my
\(A=\frac{1}{2}(B+B+2my)y\).
\(A=\frac{1}{2}(2B+2my)y\).
A= (B+my)y
\(P =B+2y\sqrt{m^{2}+1}\).
substituting, \(B=\frac{A}{y}-my\).
\(P =\frac{A}{y}-my+2y\sqrt{m^{2}+1}\). …..(1)
There are 3 variables y, B, m.
For a given area is perimeter is to be minimum
\(\frac{\mathrm{d} P}{\mathrm{d} y}=0\).
\(\frac{\mathrm{d} P}{\mathrm{d} y}=\frac{-A}{y^{2}}-m+2\sqrt{m^{2}+1}\).
\(0=\frac{-A}{y^{2}}-m+2\sqrt{m^{2}+1}\).
\(\frac{A}{y^{2}}+m=2\sqrt{m^{2}+1}\).
\(A=y^{2}[2\sqrt{m^{2}+1}-m]\). …..(2)
form equation 1 & 2
\(P =\frac{y^{2}[2\sqrt{m^{2}+1}-m]}{y}-my+2y\sqrt{m^{2}+1}\).
\(P =4y\sqrt{m^{2}+1}-2my\).
For efficient channel section with varying slope
\(\frac{\mathrm{d} P}{\mathrm{d} \theta }=0\).
\(\frac{\mathrm{d} P}{\mathrm{d} \theta }=4y\cdot \frac{1}{2}\cdot \frac{0+2m}{\sqrt{1+m^{2}}}-2m\).
\(4y\cdot \frac{1}{2}\cdot \frac{0+2m}{\sqrt{1+m^{2}}}-2m=0\).
\(2y(\frac{2m}{\sqrt{1+m^{2}}}-1)=0\).
\(\frac{2m}{\sqrt{1+m^{2}}}-1=0\).
\(\frac{2m}{\sqrt{1+m^{2}}}=1\).
\(2m=\sqrt{1+m^{2}}\).
Taking the square of both sides, this equation becomes
4m2= 1+m2
3m2= 1
m=\(\frac{1}{\sqrt{3}}\)
tanθ = \(\frac{1}{m}=\sqrt{3}\)
θ= 60°
For economical trapezoidal section with varying side slope m, the value of side slope should be m=\(\frac{1}{\sqrt{3}}\). (1:m)(V:H)
For most efficient trapezoidal channel section following condition should be satisfied.
- \(\frac{T}{2}\)= Length of side slope
- \(R=\frac{y}{2}\).
- (x=y) For most efficient trapezoidal channel section, a circle of radius y shall be inscribed in the trapezoidal section.
- θ= 60°
- \(B=\frac{2y}{\sqrt{3}}\).
- \(T=\frac{4y}{\sqrt{3}}\).
- \(A=\sqrt{3}y^{2}\).
- \(P=\frac{6y}{\sqrt{3}}\).
- \(D=\frac{A}{T}=\frac{3y}{4}\).
Note.1
1.
2.
3.
4.
5.
\(\frac{T}{2}\)= Length of side slope
length of side slope= \(y\sqrt{m^{2}+1}\).
\(\sqrt{m^{2}}=\frac{1}{3}\).
length of side slope= \(y\sqrt{\frac{1}{3}+1}\)
length of side slope= \(\frac{2y}{\sqrt{3}}\)
\(\frac{T}{2}=\frac{2y}{\sqrt{3}}\)
T=B+2my
\(\frac{B+2my}{2}=\frac{2y}{\sqrt{3}}\)
\(B=\frac{4y}{\sqrt{3}}-\frac{2y}{\sqrt{3}}\)
\(B=\frac{2y}{\sqrt{3}}\)
6.
T=B+2my
\(B=\frac{2y}{\sqrt{3}}\)
m=\(\frac{1}{\sqrt{3}}\)
\(T=\frac{2y}{\sqrt{3}}+\frac{2y}{\sqrt{3}}\)
\(T=\frac{4y}{\sqrt{3}}\)
7.
A= (B+my)y
\(B=\frac{2y}{\sqrt{3}}\)
m=\(\frac{1}{\sqrt{3}}\)
\(A=(\frac{2y}{\sqrt{3}}+\frac{y}{\sqrt{3}})y\)
\(A=(\frac{3y}{\sqrt{3}})y\)
\(A=\sqrt{3}y^{2}\).
8.
\(P =B+2y\sqrt{m^{2}+1}\).
\(B=\frac{2y}{\sqrt{3}}\)
\(P =\frac{2y}{\sqrt{3}}+2y\sqrt{m^{2}+1}\).
m2=1/3
\(P =\frac{2y}{\sqrt{3}}+2y\sqrt{\frac{1}{3}+1}\).
\(P =\frac{2y}{\sqrt{3}}+2y\sqrt{\frac{4}{3}}\).
\(P =\frac{2y}{\sqrt{3}}+\frac{4y}{\sqrt{3}}\).
\(P =\frac{6y}{\sqrt{3}}\).
Note.2
⇒ We know that bottom width \(B=\frac{2y}{\sqrt{3}}\) & length of side slope= \(\frac{2y}{\sqrt{3}}\) are same with side slope θ= 60° which is the properties of hexagon.
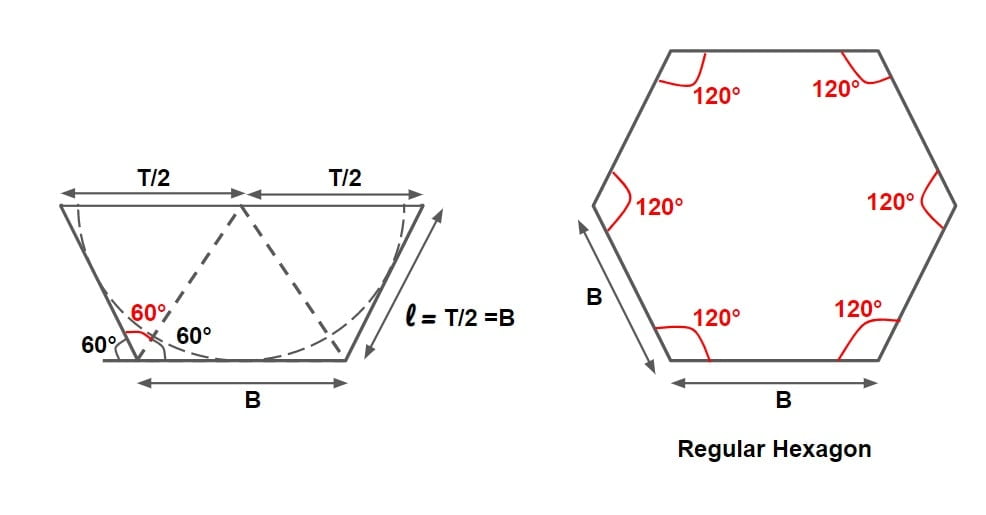 ⇒ Thus a most efficient trapezoidal channel is half of regular hexagon.
⇒ Thus a most efficient trapezoidal channel is half of regular hexagon.
4. Most Efficient Circular Section
⇒ Consider a circular section of radius R, and depth of flow= d.
⇒ In a circular section the shape of flow cross section varies with the depth of flow. Due to the divergence and convergence, the depth required to achieve maximum discharge and maximum velocity will be different.
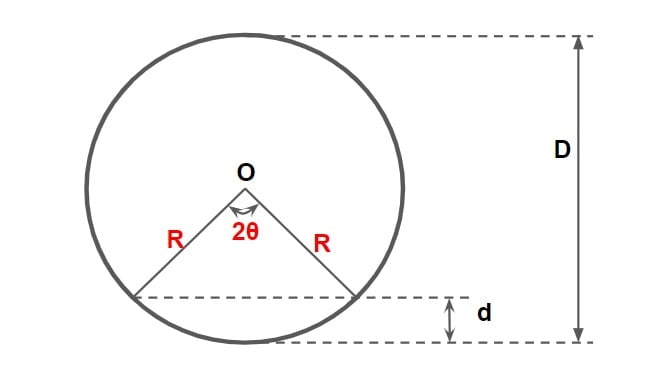
From Manning’s Equation
For condition for maximum discharge
2θ= 302°22′ or \(\frac{d}{D}=0.938\).
d= R(1-cosθ)
For condition for maximum velocity
2θ= 257°27′ or \(\frac{d}{D}=0.81\).
d= R+ R·cos(180°-θ)
From Chezy’s Equation
For condition for maximum discharge
2θ= 308° or \(\frac{d}{D}=0.95\).
d= R(1-cosθ)
For condition for maximum velocity
2θ= 257°27′ or \(\frac{d}{D}=0.81\).
d= R+ R·cos(180°-θ)
Properties of Most Efficient Channel Section of Different Shapes:
| Channel Area | Rectangle | Triangle | Trapezoidal |
| Area | A=2y2 | A=y2 | \(A=\sqrt{3}y^{2}\). |
| Wetted Perimeter | P=4y | \(P=2\sqrt{2}y\). | \(P=\frac{6y}{\sqrt{3}}\). |
| Hydraulic Radius | R= y/2 | \(R=\frac{y}{2\sqrt{2}}\). | \(R=\frac{y}{2}\). |
| Width | B=2y | \(B=\frac{2y}{\sqrt{3}}\). | |
| Top Width | T =2y | T=2y | \(T=\frac{4y}{\sqrt{3}}\). |
| Hydraulic Depth | D=A/T=y | D = \(\frac{y}{2}\) | \(D=\frac{A}{T}=\frac{3y}{4}\). |
Type of Channel According to Efficiency
There are two type of a channel.
- Type.1
- Type.2
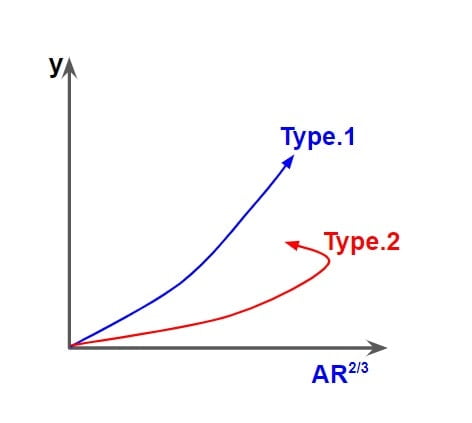
Type.1
⇒If the top surface width of flow is increase when increase the depth of flow then the channel is called Type.1 channel. Example: Rectangle, Triangle∇, Trapezoidal.
⇒For most efficient channel either
Q→ Maximum i.e \(\frac{\mathrm{d} Q}{\mathrm{d} Y}=0\)
P→ Minimum \(\frac{\mathrm{d} P}{\mathrm{d} Y}=0\)
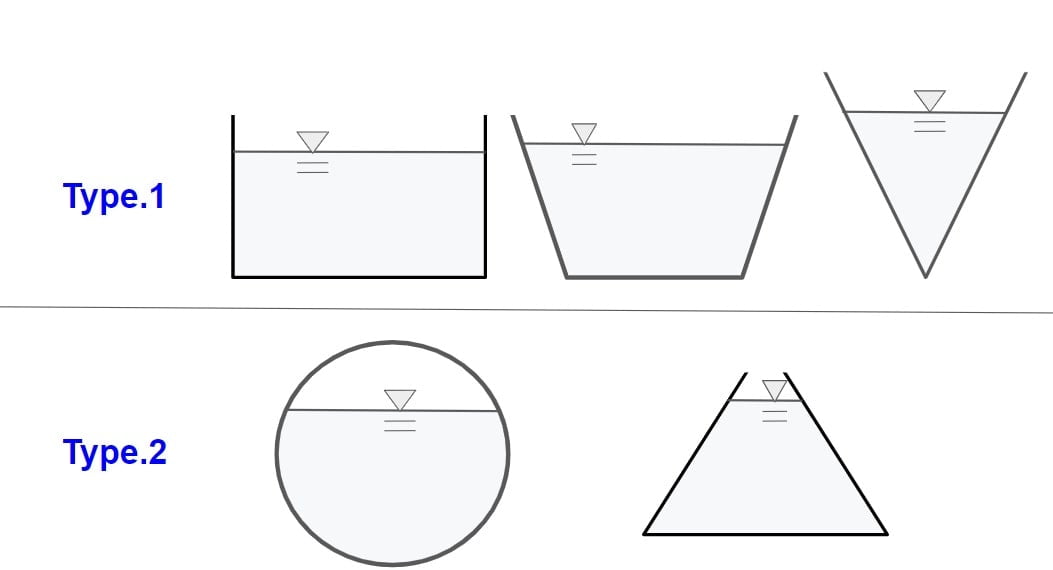
Type.2
⇒If the top surface width of flow is decrease when increase the depth of flow then the channel is called Type.2 channel. Example: CircularΟ, TriangleΔ.
⇒For most efficient channel only
Q→ Maximum i.e \(\frac{\mathrm{d} Q}{\mathrm{d} Y}=0\)
we will not do perimeter minimization for type.2 channel.
⇒By Manning’s Equation
\(Q= \frac{A\cdot R^{2/3}\cdot S_o^{1/2}}{N}\).
Shear Stress On The Boundary Of Uniform Flow In Open Channel Flow
By applying the momentum equation to a control volume encompassing Sections 1 and 2, distance L apart, as shown in Fig.

P1 − W sin θ − Ff− P2= M2− M1
where
P1 & P2 = pressure forces at sections 1 and 2 respectively
M1 & M2 = momentum fluxes at sections 1 and 2 respectively
W = weight to fluid in the control volume
Ff = shear force at the boundary.
Since the flow is uniform,
P1 = P2 ,
& M1 = M2
So
P1 − W sinθ − Ff− P2= M2− M1
W·sinθ = Ff
W·sinθ
W=γ·A·L
(γ=W/volume)
for small slopes: sinθ= tanθ = SO
W·sinθ= γ·A·L·SO
γ·A·L·SO= Ff
Assuming uniform shear stress along the bed and side slope so
Ff= τo×Area
Ff= τo×P·L
(τ0 = average shear stress acting over channel boundary)
(τ0 = average shear stress on the wetted perimeter P of length L)
γ·A·L·SO= τo×P·L
τo= γ·(A/P)·SO
A/P=R
| τo= γ·R·SO |
τo= shear stress at boundary.

| τb= γ·R·SO |
τb= Bed shear stress or drag.
| τs= 0.75×γ·R·SO |
τs=side shear stress
shear velocity or friction velocity, vτ = \(\sqrt{\frac{\tau _o}{\rho }}\)
vτ = \(\sqrt{g\cdot R\cdot S_o}\)
\(\sqrt{R\cdot S_o}=\frac{v_\tau }{\sqrt{g}}\) ……(1)
Note: By chezy’s equation
\(v=c\sqrt{RS_o}\).
\(\sqrt{RS_o}=\frac{v}{c}\) ……(2)
From equation 1 & 2
\(\frac{v}{c}=\frac{v_\tau }{\sqrt{g}}\)
c=\(\sqrt{\frac{8g}{f}}\)
\(v_\tau=\frac{v}{c}\sqrt{g}\).
\(v_\tau=\frac{v}{\sqrt{8g}}\sqrt{g}\sqrt{f}\).
| \(v_\tau=\frac{\sqrt{f}}{\sqrt{8}}v\). |
f= friction factor