Introduction  

Many surveys have the primary goal of finding the area of the surveyed tract and the amount of earthwork.

  Measurement of Area  

• The method adopted for measurement of area and volume depends upon
  1. Accuracy required
  2. Shape/ Geometry of track.
• Measurement can be done by either
  1. By field measurement
  2. By plan measurement
• If the plan is enclosed by a straight line, it can be divided into geometrical figures, like: triangle, rectangle, square etc. The area of these figures can be determined by using standard formulas.
• But if the boundaries are irregular, then approximate methods are being used.

Note: Planimeter meter is used to determine areas of irregular shape.

Computation of Area of Geometrical Figures

1.Rectangle	Area= length(L) × width(b)
2.Square	Area= length(L) × width(b)
3.Triangle	Area= half of the base(b) × perpendicular height(h)
4.Circle	Area = Π × (Radius)2
5.Parallelogram	Area= base × perpendicular height
6.Trapezoid	Area= half of the sum of parallel sides ×  perpendicular height

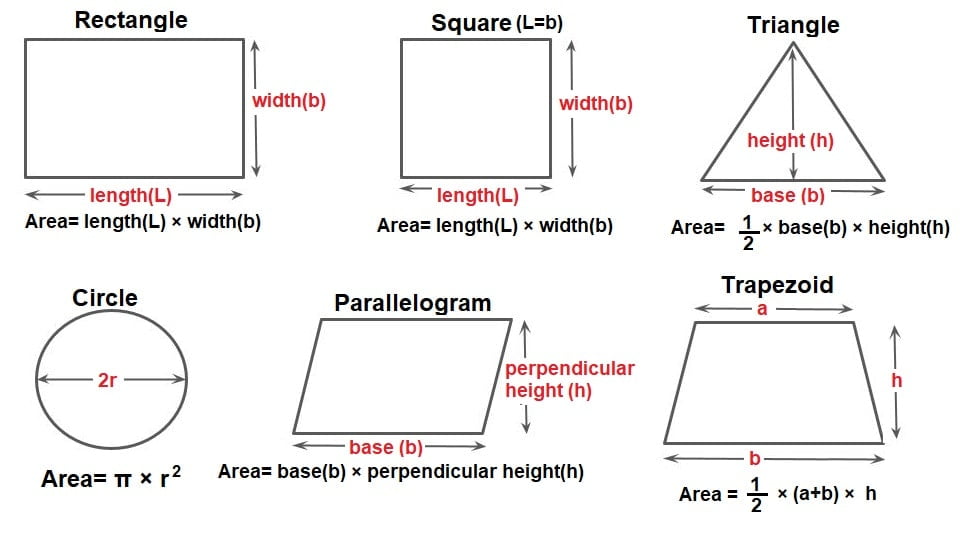
7.Trapezium

Area (ABCD) = Area(ABC) + Area(ACD)

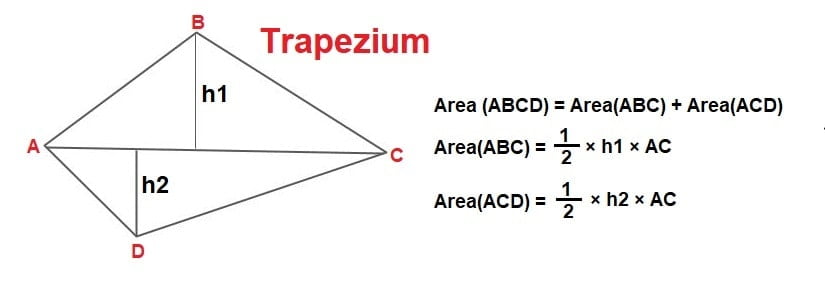
8.Oblique Triangle

\(A=\sqrt{s(s-a)(s-b)(s-c)}\)

where a, b, care the sides.

\(s=\frac{a+b+c}{2}\)

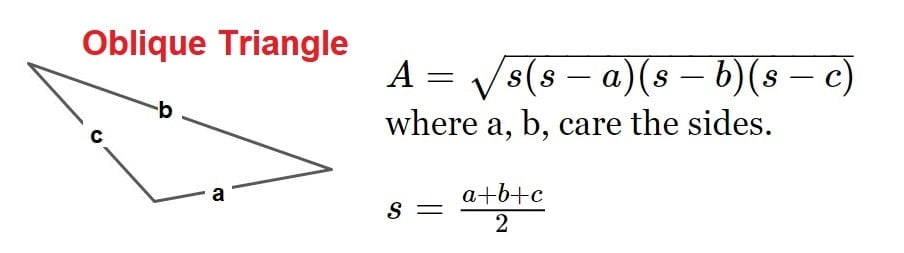
9.Area of a Segment

Area of segment (ACB) = Area of sector (ACBO) – Area of triangle (AOB)

\(A=\frac{\Pi R^{2}}{360^{\circ}}\times \alpha -\frac{1}{2}\times 2Rsin\frac{\alpha }{2}\times Rcos\frac{\alpha }{2}\)

\(A=R^{2}\left ( \frac{\Pi \alpha }{360^{\circ}} -\frac{sin}{2}\right )\)

\(A=R^{2}\left ( \frac{\Pi \alpha }{360^{\circ}} -\frac{sin}{2}\right )\)

 

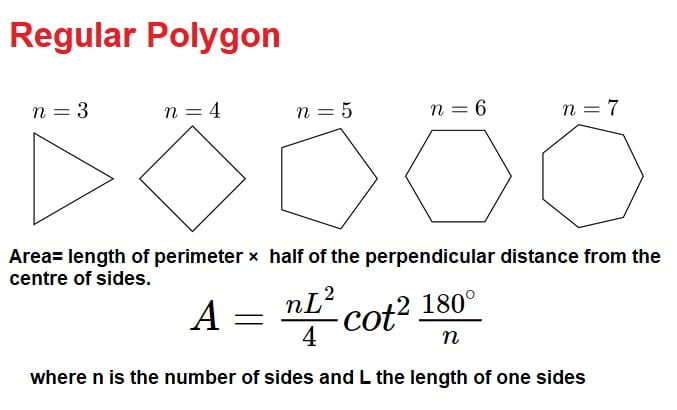
10.Regular Polygon

Area= length of perimeter ×  half of the perpendicular distance from the centre of sides.

\(A=\frac{nL^{2}}{4}cot^{2}\frac{180^{\circ}}{n}\)

\(A=\frac{nL^{2}}{4}cot^{2}\frac{180^{\circ}}{n}\)

where n is the number of sides and L the length of one sides

---

Computation of Area of Irregular Shape

1.Mid Ordinate Rule

If offsets h₁, h₂, …., h_n-1. are measured at the mid point of each division.

Area = average ordinate × length of base.

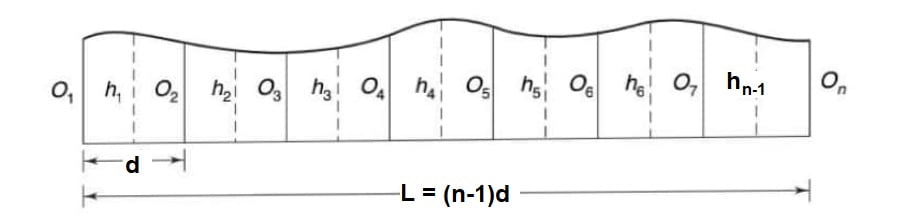
\(A=\frac{h_1+h_2+….+h_{n-1}}{n-1}L\).

∴L=(n-1)d

\(A=\frac{h_1+h_2+….+h_{n-1}}{n-1}(n-1)d\)

\(A=(h_1+h_2+…+h_{n-1})d\)

where

n-1 = number of division

d = distance between the two perpendicular offsets.

L = length of base line {L=(n-1)d}

2.Average Offset Rule

If offsets O₁, O₂, …., O_n. are measured at the mid point of each division and spaced apart at equal distance d.

Area = average of all ordinate × length of base.

\(A=\frac{O_1+O_2+….+O_n}{n}L\)

\(A=\frac{O_1+O_2+….+O_n}{n}(n-1)d\)

\(A=\frac{(n-1)d}{n}\Sigma O_i\)

3.Trapezoidal Rule

The accuracy of this method is more than mid-ordinate and average ordinate method.

Area of first trapezoid \(=\frac{O_1+O_2}{2}d\).

Area of second trapezoid \(=\frac{O_2+O_3}{2}d\).

Area of last trapezoid \(=\frac{O_{n-1}+O_n}{2}d\).

Total area of trapezoid

\(A=\frac{1}{2}(O_1+O_2)d+\frac{1}{2}(O_2+O_3)d+….+\frac{1}{2}(O_{n-1}+O_n)d\)

\(A=\frac{1}{2}d[O_1+2O_2+2O_3+2O_{n-1}+O_n]\)

\(A=d[\frac{O_1+O_N}{2}+O_2+O_3+…O_{n-1}]\)

4.Simpson’s One Third Rule

• If the boundaries of irregular tract are curved then Simpson method is preferred over the trapezoidal rule to calculate the area of given track.
• In this the curved boundary is considered to be a parabolic arch.

\(A=\frac{d}{3}[(O_1+O_n)+4(O_2+O_4+…+O_{n-1})+2(O_3+O_5+…+O_{n-2})]\)

Note

• To apply Simpson’s rule offsets should be odd in number.
• To work with even no of offsets Simpson’s should be apply upto last offsets and remaining area should be calculated using trapezoidal rule.

---

  Measurement Of Volume 

The computation of the volume of different quantities is required for planning & designing  of various engineering work .

1. Earthwork for highway, railway, retaining walls.
2. Volume for reservoir capacity
3. Concreting work
4. Storage requirement

Computation of Volume of Irregular Shape

1.Trapezoidal Rule / End Area Method

This method is also called as end are method.

\(V=d[\frac{A_1+A_n}{2}+A_2+A_3+…A_{n-1}]\)

2.Prismoidal / Simpson’s  Rule

\(V=\frac{d}{3}[(A_1+A_n)+4(A_2+A_4+…+A_{n-1})+2(A_3+A_5+…+A_{n-2})]\)

Note

• This formula usually gives less volume than trapezoidal formula.
• This formula is not suitable for rock excavation and concrete work.
• To apply Simpson’s rule offsets should be odd in number.
• To work with even no of offsets Simpson’s should be apply upto last offsets and remaining volume should be calculated using trapezoidal rule.

FOR MORE INFORMATION ABOUT SURVEYING