Vertical Curve
- Vertical Curve are provided at the intersections of different grades to smoothen the vertical profile.
- The vertical curve used in the highway are of two types
- Summit Curve
- Valley Curve
Note: This topic is part of the second chapter of Highway Engineering. I suggest reading this topic in the context of the complete chapter: Geometric Design of Highway. If you want to read the entire Highway Engineering, click here: Highway Engineering.
Summit Curve

- Summit curve are vertical curve with convexity upward & concavity downward.
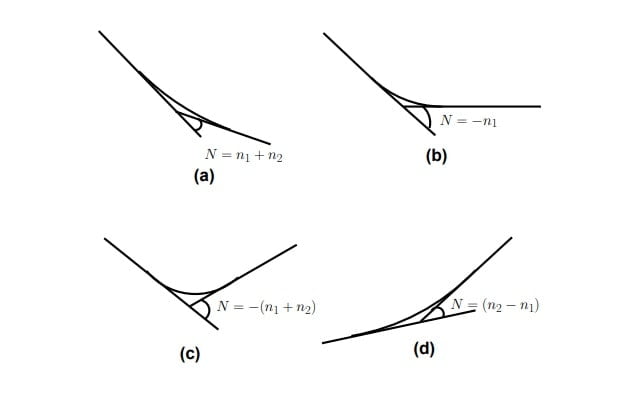
- It can formed by two gradient in following ways.
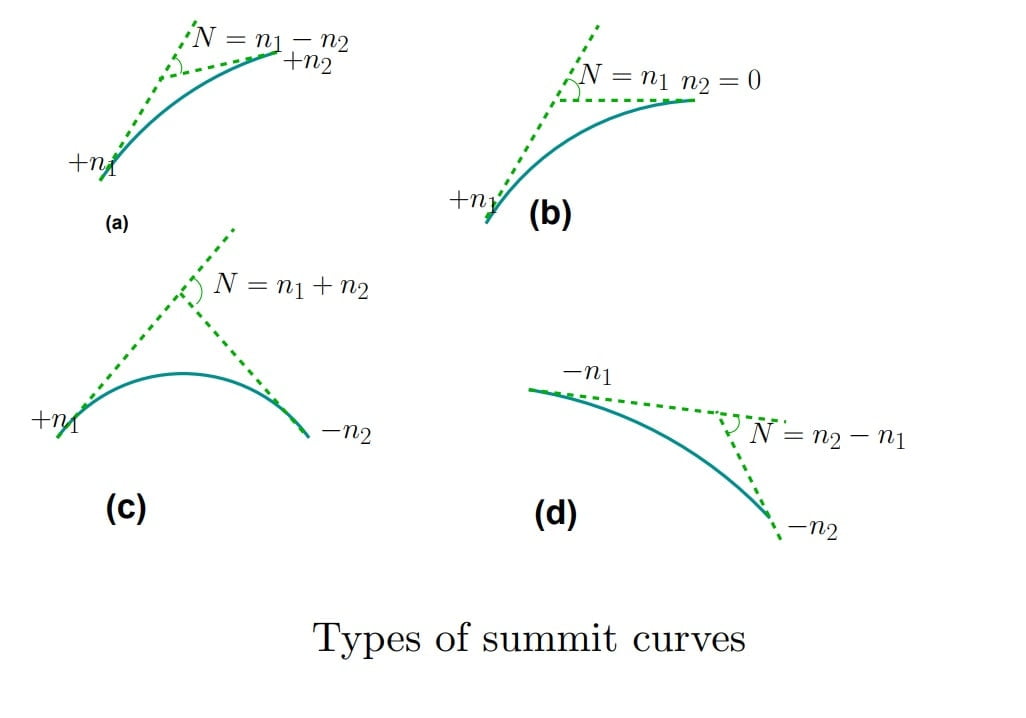
Some Important Points of Summit Curve
- Convexity upward & Concavity downward.
- Vertical Point Of Intersection (VPI) always lies above the curve.
- Summit curve are designed only for sight distance criteria.
- Summit curve are made with square parabola shape.
- Ideal shape of summit curve is circular.
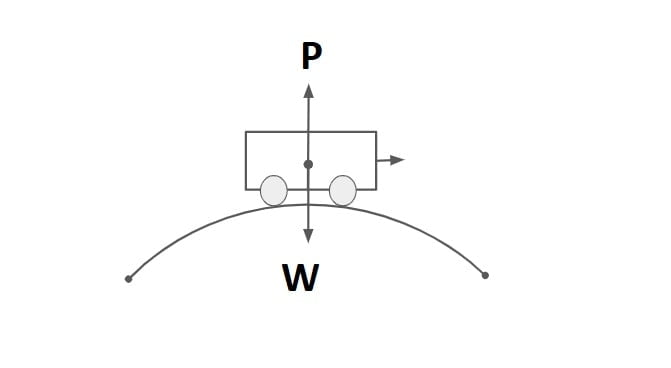
- Centrifugal force acts in upwards direction due to which effective weight of vehicle reduces. Hence there is no discomfort in summit curve.

Derivation of Summit Curve
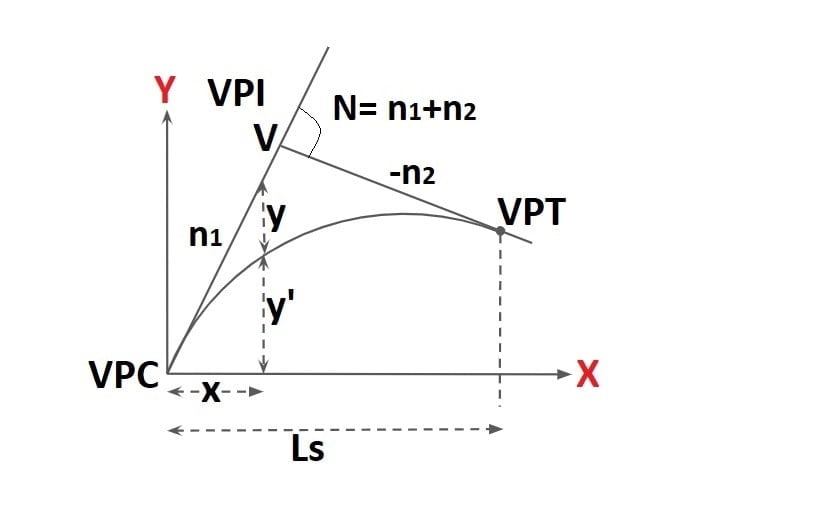
 1.General Equation of Summit Curve
1.General Equation of Summit Curve
y’= ax2 + bx + c
At point A, (y’=0, x=0)
then we put the value of (y’=0, x=0)
0= 0+0+c
c=0
y’= ax2 + bx + 0
y’= ax2 + bx
\(\frac{\mathrm{d} y’}{\mathrm{d} x}= 2ax+b\)=Gradient
At point A, x=0, \(\frac{\mathrm{d} y’}{\mathrm{d} x}= +n_1\)
+n1=2a·0+b
b=+n1
At point B, x= LS, \(\frac{\mathrm{d} y’}{\mathrm{d} x}= -n_2\)
-n2=2a·LS + n1
\(a=-[\frac{n_1+n_2}{2L_S}]\).
\(a=-[\frac{N}{2L_S}]\)
General Equation
\(y’=[-\frac{N}{2L_S}]x^{2}+n_1x\)
2.Position of Summit / Highest / Crest Point of Curve From VPC
we know that at crest point of curve, slope is zero.
\(\frac{\mathrm{d} y’}{\mathrm{d} x}=0\)2ax+b=0
x=-b/2a
we know that
b=+n1 & \(a=-[\frac{N}{2L_S}]\).
so \(x=\frac{n_1}{N}L_S\)
3.Apex Equation of Summit Curve
tanθ= n1 = (y+y’)/x
y= n1x-y’
\(y’=[-\frac{N}{2L_S}]x^{2}+n_1x\)
\(y= [n_1x-([-\frac{N}{2L_S}]x^{2}+n_1x)\)
\(y= [\frac{N}{2L_S}]x^{2}\)
4.Position pf VPI from VPC
 From ΔAVE
From ΔAVE
tanθ1=n1=VE/x
VE= n1x…….(1)
From ΔVDB
tanθ2=n2=VD/(LS-x)
VD= n2LS – n2x…….(2)
y’B = DE = VE- VD……..(3)
\(y’_B=[-\frac{N}{2L_S}]x^{2}+n_1x\) (x= LS) ……(4)
the value of VE, VD, y’B from equation 1,2,4 put in Equation 3.
x=LS/2
Case-1: When curve is symmetrical (n1=n2)
- Vertical line passing through VPI will bisect length of curve into two equal half.
- This line always pass through summit point of curve.
- In this case R.L of starting point & end point will be same.
Case-2: When curve is unsymmetrical (n1≠n2)
- Vertical line passing through VPI will bisect length of curve into two equal half.
- This line will never pass through summit point of curve.
- In this case the curve will be tilted & R.L of starting point & end point will be different.
5.Calculating Ordinates of Summit Curve
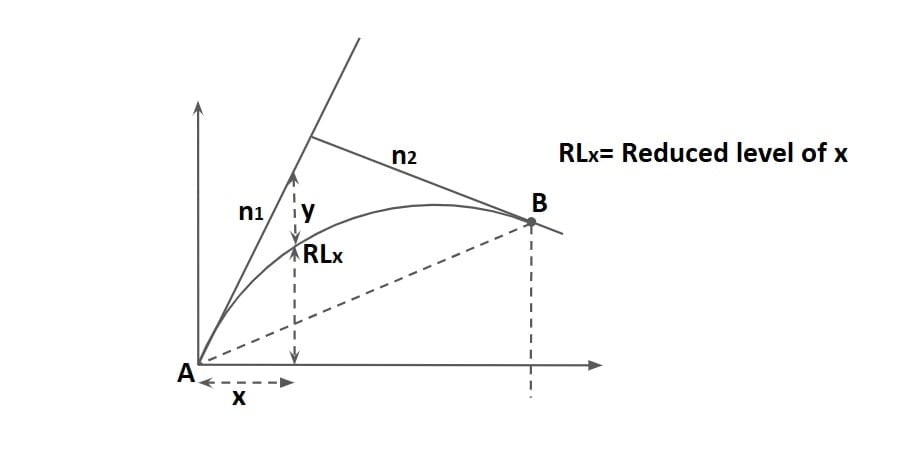 RL of a point at a distance x
RL of a point at a distance x
RLx = (RL of A) + n1x – y
RLx = (RL)A + n1x – (Nx2/2L )
RLB = (RL)A + n1L – (NL2/2L )
Length Of Summit Curve
Case-1: When LS> SD (Sight Distance)
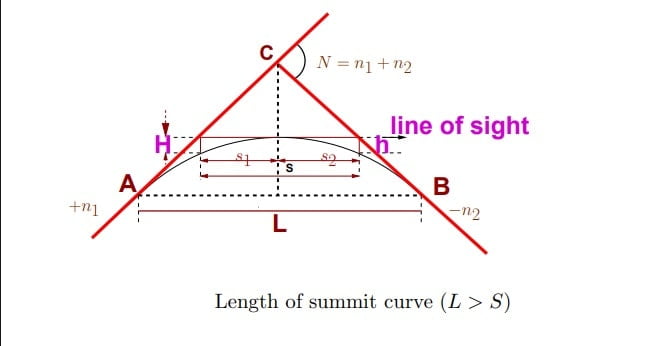 H= height of drivers eye
H= height of drivers eye
h= height of obstruction
s= sight distance
\(L_S=\frac{N\cdot s^{2}}{2(\sqrt{H}+\sqrt{h})^{2}}\).
As per IRC
for SSD, H= 1.2m, h= 0.15m.
\(L_S=\frac{N\cdot s^{2}}{4.4}\)for OSD/ISD, H=1.2m, h=1.2m.
\(L_S=\frac{N\cdot s^{2}}{9.6}\)Case-2: When LS< SD (Sight Distance)
 \(L_S=2s-\frac{2(\sqrt{H}+\sqrt{h})^{2}}{N}\).
\(L_S=2s-\frac{2(\sqrt{H}+\sqrt{h})^{2}}{N}\).
As per IRC
for SSD, H= 1.2m, h= 0.15m.
\(L_S=2s-\frac{4.4}{N}\)for OSD/ISD, H=1.2m, h=1.2m.
\(L_S=2s-\frac{9.6}{N}\)Note:
For calculation of sight distance in design of summit curve & valley curve, effect of gradient should not be taken.
hence
\(SSD= 0.2Vtr + \frac{V^{2}}{254f}\)Valley Curve
- Valley curve are vertical curve with concavity upward & convexity downward.
- It can formed by two gradient in following ways.

Some Important Points of Valley Curve
1.Convexity downward & Concavity upward.
2.Vertical Point Of Intersection (VPI) always lies below the curve.
3.Valley curves are designed taking following consideration into account
- Comfort to passengers
- Headlight sight distance
- Drainage in valley curve
Note:
Maximum Distance visible through Head light of vehicle is called Head Light Sight Distance.
Generally HSD = SSD
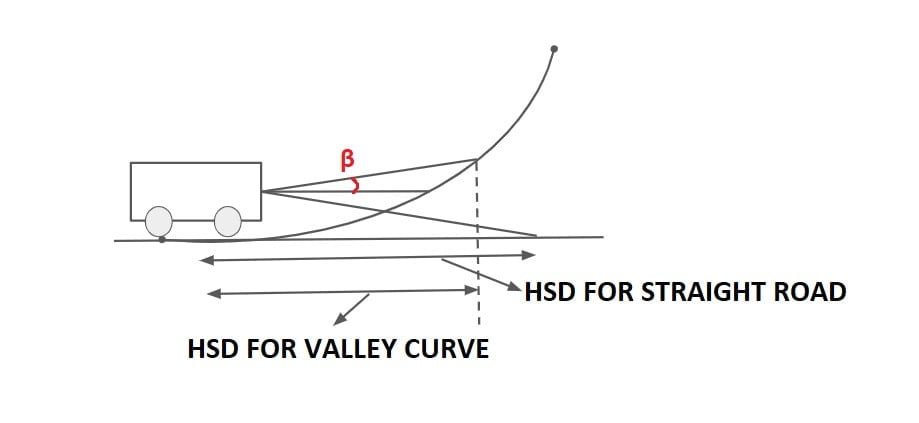 As per IRC
As per IRC
- height of head light =h=0.75m
- Beam angle = β=1°
4.Valley Curves is usually made up of two transition curve of equal length without having a circular curve in between.
5.In valley curve, centrifugal force and gravity force both acts downward, hence create discomfort for passengers.
6.Position of lowest point of valley curve from starting of curve.
\(x=L_V(\frac{n_1}{2N})^{\frac{1}{2}}\)
LV= length of valley Curve
N= Change in Gradient
n1= 1st gradient.
Length Of Valley Curve
Length of valley curve is designed on the basis of max of following two criteria.
Criteria 1: As per Comfort Condition
In this criteria the rate of change of centrifugal acceleration is limited to a comfortable zone of about 0.6m/sec3, then the length of transition curve is given by
\(L_T=\frac{v^{3}}{CR}\)……(1)
and \(R=\frac{L_T}{N}\)………(2)
the value of R from equation 2 put in equation 1.
\(L_T=\sqrt{\frac{Nv^{3}}{C}}\)and LV = 2LT
\(L_V=2\sqrt{\frac{Nv^{3}}{C}}\)As per IRC
c= 0.6m/s3 for cubic parabola
v= change in speed
N = change in gradient
unit change:
\(L_V=0.378\sqrt{Nv^{3}}\)
v in kmph
LV in m
Criteria 2: As per HSD
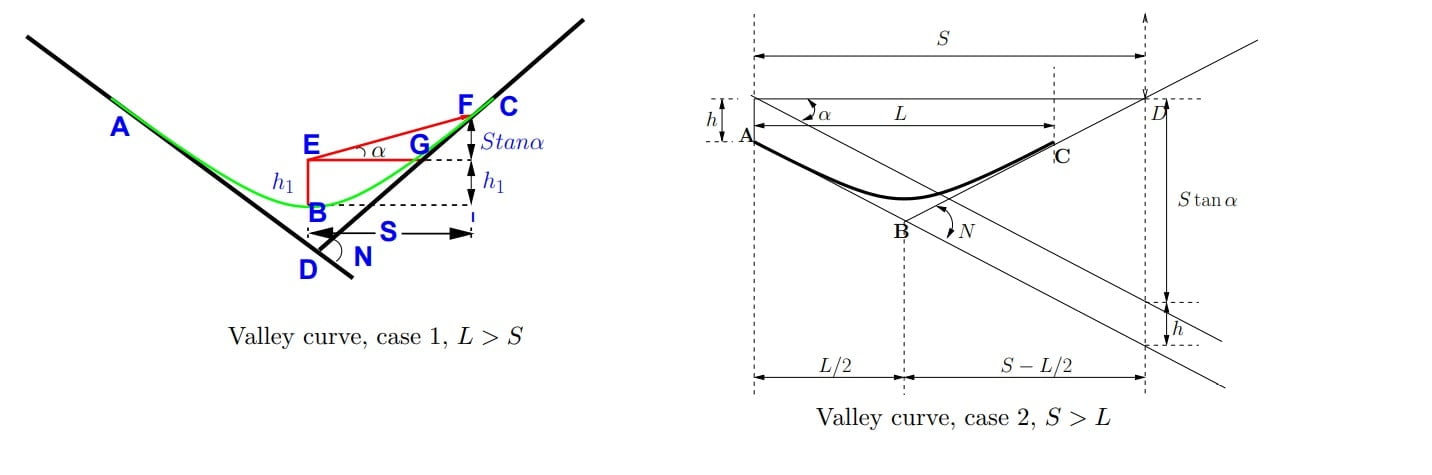
 Case-1: When LV> HSD
Case-1: When LV> HSD
s= HSD of horizontal
β= Beam angle
h= height of headlight
\(L_V=\frac{N\cdot s^{2}}{2h+2\cdot s\cdot tan\beta }\).
As per IRC
for β=1°, h= 0.75m.
\(L_V=\frac{N\cdot s^{2}}{1.5+0.035\cdot s }\).
Case-2: When LV< HSD
\(L_V=2s -\frac{2h+2s\cdot tan\beta }{N}\).
As per IRC
for β=1°, h= 0.75m.
\(L_V=2s -\frac{1.5+0.035\cdot s}{N}\).
 1.General Equation of Summit Curve
1.General Equation of Summit Curve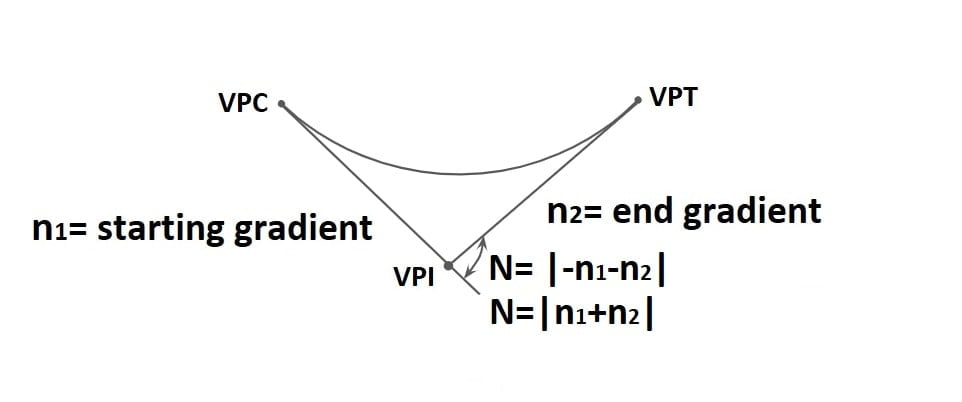
 Case-1: When LV> HSD
Case-1: When LV> HSD
Basically I am an civil Engineer.Working on National Highways since last 30 years.
Sir , Your knoweldge is super and I Am very happy to read your content.