Contents

Transition Curves:

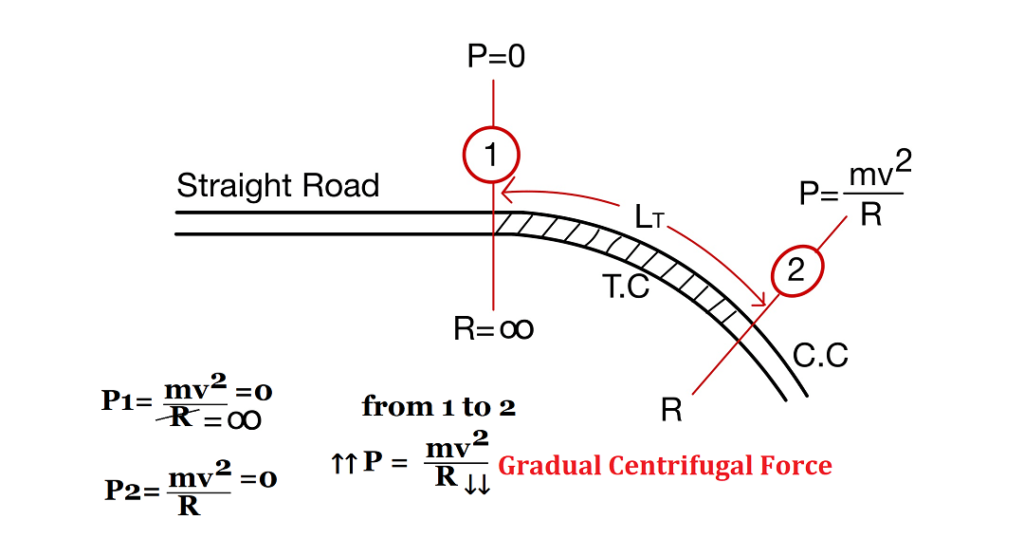
When a vehicle traveling on a straight road enters into a horizontal curve instantaneously, it will ca discomfort to the driver. To avoid this, it is required to provide a transition curve. This may be provided either between a tangent and a circular curve or between two branches of a compound or reverse curve.

Transition curve has a radius equal to infinite when it meets to straight Road within gradually change to designate radius towards the circular curve.

Note: This topic is part of the second chapter of Highway Engineering. I suggest reading this topic in the context of the complete chapter: Geometric Design of Highway. If you want to read the entire Highway Engineering, click here: Highway Engineering.

The objectives of providing a transition curves are:

To gradually introduce the centrifugal force between straight and circular curves.
To avoid the certain jerk.
To gradual introduction of superelevation and extra widening.
To enable the driver turn the sheering gradually for comfort and security.
To improve aesthetic appearance.

A transition curve should salisty the following conditions

It should meet the straight path tangentially.
It should meet the circular curve tangentially.
It should have the same radius as that of the circular curve at its junction with the circular curve.
The rate of increase of curvature and superelevation should be the same.

The length of transition curve required on a horizontal highway curve depends upon the following factors:

Radius of circular curve, R
Design speed, V
Allowable rate of change of centrifugal acceleration, C
Maximum amount of super elevation, E which depends on the maximum rate of superelevation, e and the total width of the pavement, B at the horizontal curve.
Rotation of pavement cross-section either about the inner edge or the centre line

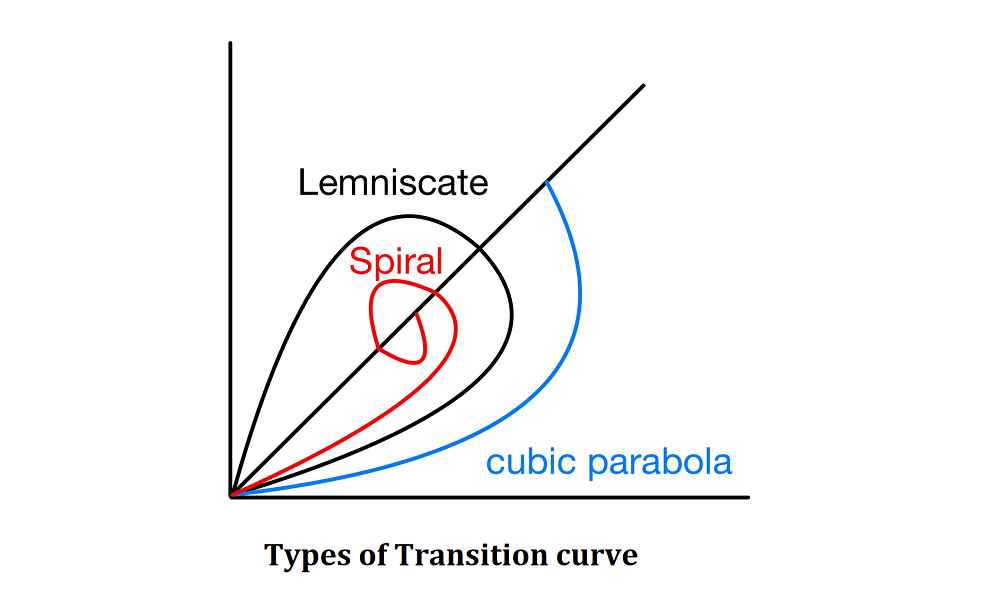
Different Types of Transition Curves

The types of transition curves commonly adopted in horizontal alignment of highways are:

1.Spiral

2.Bernoulli’s Lemniscate

3.Cubic Parabola

NOTE:

In all these curve the radius decreases at length increases.
But the rate of change of radius or rate of change of centrifugal force is not constant in case of Lemniscate and cubic parabola.
Hence a spiral curve is used as transition curve as it fulfills the requirement of ideal transition curve.
According to IRC an ideal transition curve is spiral because rate of change of radial acceleration (C) remains constant.

Length of Transition Curve

The length of transition curve is designed to fulfill three conditions:

Rate of change of centrifugal acceleration to be developed gradually
Rate of introduction of the designed superelevation to be at a reasonable rate, and
Minimum length by IRC empirical formula

The length of transition curve following three conditions:

Length of Transition Curve by the Rate of Change of Radial Acceleration

Length of Transition Curve is designed such that the rate of change of centrifugal force is low.

Rate of change of centrifugal acceleration:

v=Velocity of the vehicle in m/s	R= Radius of the curve in m
C= rate of change of radial acceleration in m/sec3	LT= Length of Transition Curve in m
t= time taken by vehicle in second to travel the transition length at speed v.

\(C=\frac{\Delta a}{T}=\frac{a_f-a_i}{T}\) \(C=\frac{\frac{v^{2}}{R}-0}{\frac{L_T}{v}}=\frac{v^{3}}{R·L_T}\) \(C=\frac{v^{3}}{R·L_T}\)

\(L_T=\frac{v^{3}}{C·R}\)	(Here,v in m/s)
or
\(L_T=\frac{0.0215V^{3}}{C·R}\)	(Here,V in km/s)

The rate of change of centrifugal acceleration is given by an empirical formula recommended by IRC

\(C=\frac{80}{75+V}\)m³/s

(Here,V in km/s)

Subject to a maximum of 0.8 and minimum of 0.5.

Length of Transition Curve by Rate of Change of Superelevation

Rate of introduction if superelevation = 1V in NH

1= elevation provided

N= Length of Transition curve

Rate As per IRC

1:150 For Plain and Rolling terrain

1:100 For Urban /Built Up Area

1:60 For Hilly Area

The length of transition curve = N·x

where x is elevation of outer edge.

(i) When pavement is rotated about inner edge

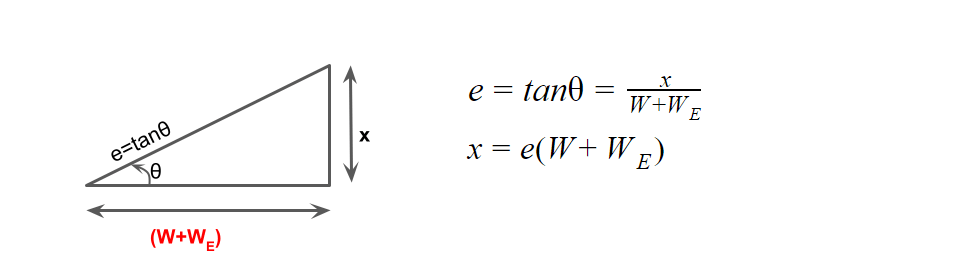
L_T=eN(W+W_E)

W=Width of pavement

W_E= Extra widening

(ii) When pavement is rotated about centre

L_T=\(\frac{1}{2}\)eN(W+W_E)

Empirical Formula for the Length of Transition Curve Recommended by IRC

For plain and rolling terrain,	\(L_T=2.7\frac{V^{2}}{R}\)
For mountainous and steep terrain,	\(L_T=\frac{V^{2}}{R}\)

V→kmph

R→m

LT→M

Setting Out of Transition Curve

When a Transition curve is introduced between a straight and circular curve, then circular curve has to be shifted so that the transition curve meets the circular curve tangentially. The shifted (S) of a circular curve is given by

\(S=\frac{L_T^{2}}{24R}\)

LT= Length of transition curve

For Detailed Analysis of Highway Engineering Step By Step.

Highway Engineering