Set Back Distance:

It is clearance distance, required from the centre line of pavement/road to the obstruction in ode to maintain the adequate sight distance to the curve.

The set back distance or clearance required from the centre line of horizontal curve depends upon.

• Required sight distance (SD)
• Radius of horizontal Curve (R)
• Length of curve(L_C)

Calculation Of Setback Distance

There are two cases in the calculation of setback distance:

Case 1: When the length of horizontal curve greater than the sight distance (L_C>SD).

(a) For Single Lane:

In single lane road the sight distance is measured along the centreline of the road.

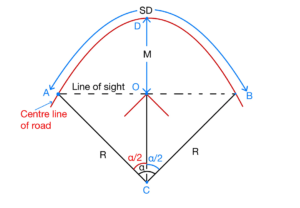
(b) For Multi lane:

In multi lane road the sight distance is measured along the centreline of the inner lane and the set back distance is measured from the centre of road.

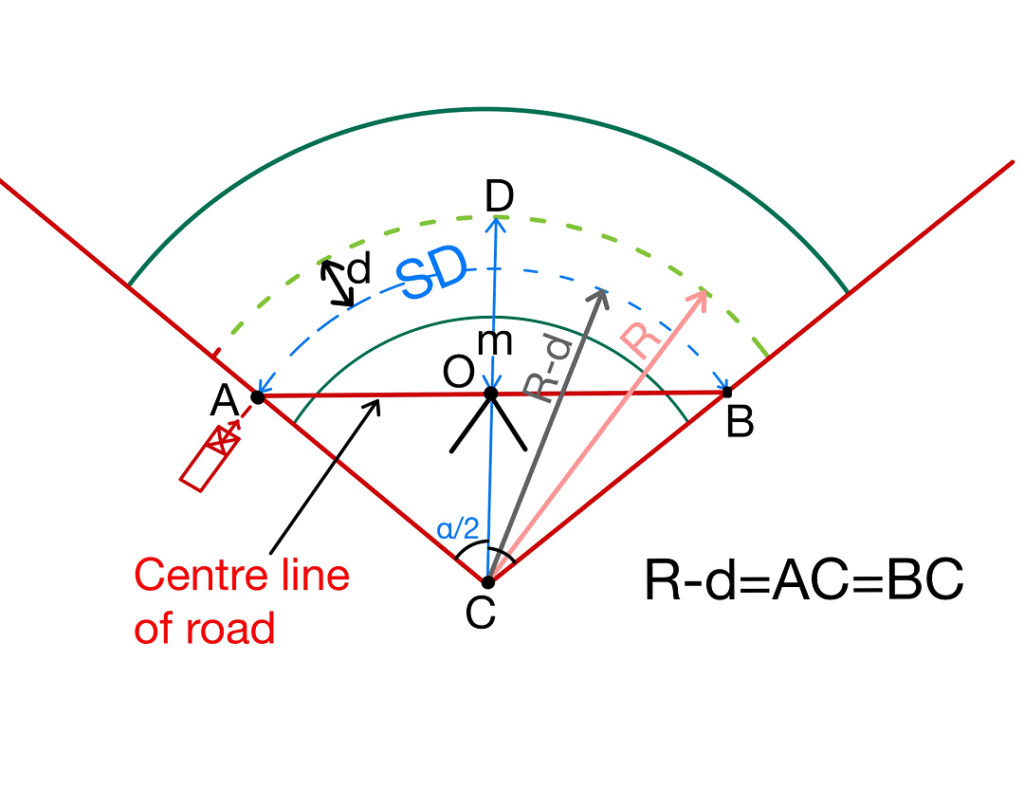
Let “d” be the distance between the centre line of road & centre line of the inside lane.

Case 2: When the length of horizontal curve less than the sight distance (L_C<SD).

(a) For Single Lane:

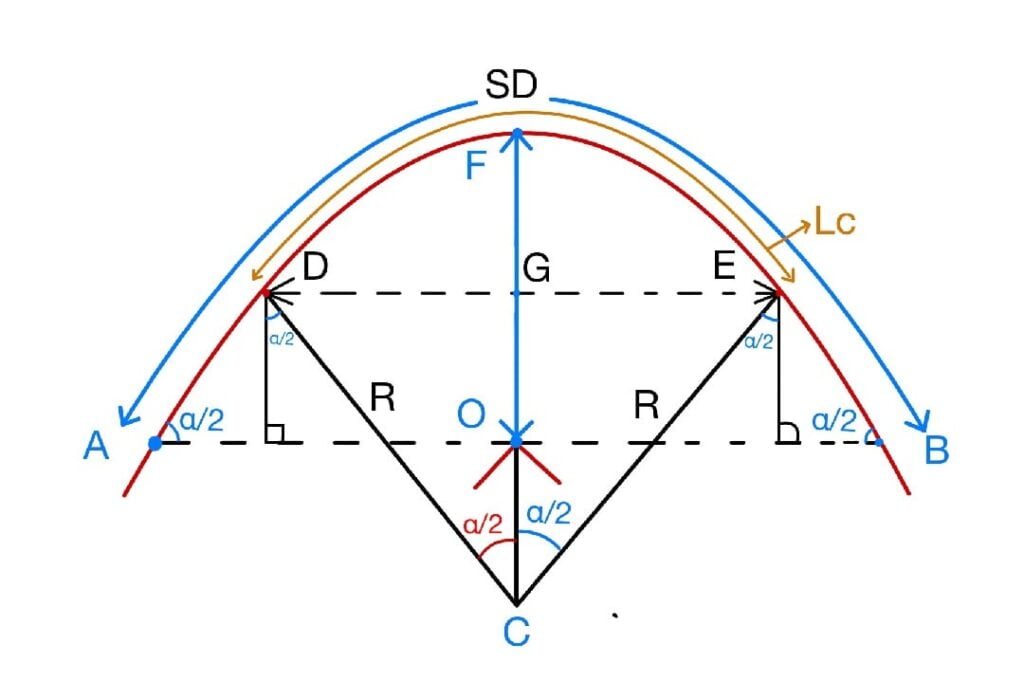
(b) For Multi lane:

\(m=R-(R-d)· cos\frac{\alpha }{2}\)+(\(\frac{SD-L_C }{2}\))\(sin\frac{\alpha }{2}\)

Here

\(\frac{\alpha }{2}=\frac{L_C}{2(R-d)}(Radians)\)

OR

\(\frac{\alpha }{2}=\frac{180}{\Pi }\frac{L_C}{2(R-d)}(Degrees)\)

Note:

Sēt back distance from central line of inner lane= m-d.

Sēt back distance from centre line of outer lane= m+d.

Sēt back distance from central line of inner edge= m-2d.

Sēt back distance from centre line of outer edge= m+2d.

In all above case two lane road is considered.

For Detailed Analysis of Highway Engineering Step By Step.

Highway Engineering