Stopping Sight Distance (SSD):
- The minimum distance visible to a driver ahead to safety stop a vehicle travelling at design speed without collision with any other obstruction is termed as “SSD”. It is also termed as “Absolute Minimum Sight Distance” or ” Non-Passing Sight Passing”.
Note: This topic is part of the second chapter of Highway Engineering. I suggest reading this topic in the context of the complete chapter: Geometric Design of Highway. If you want to read the entire Highway Engineering, click here: Highway Engineering.
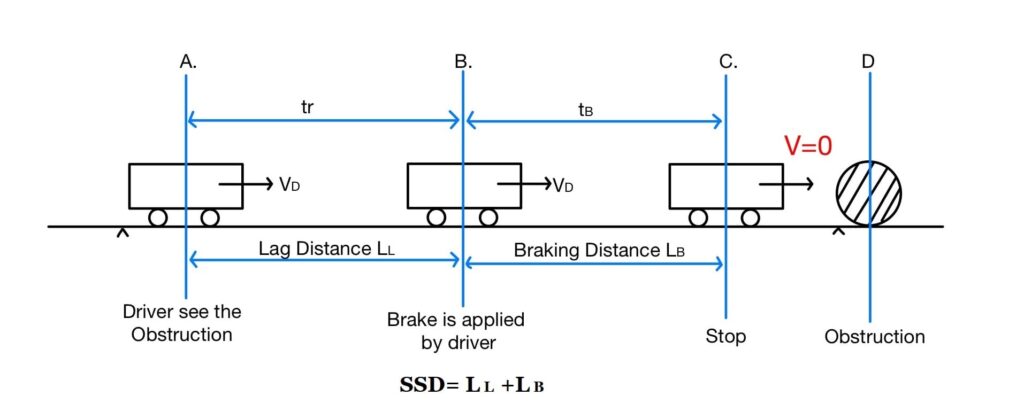
The stopping distance of vehicle include:
- Lag Distance (\(L_L\))
- Braking Distance(\(L_B\))
(I). Lag Distance (\(L_L\))
- The distance travelled by vehicle at uniform design speed during the total reaction time (tr) termed as “Lag Distance (\(L_L\)).
As per IRC reaction time is taken to be 2.5 second for SSD.
(II). Braking Distance(\(L_B\))
- The distance travelled by the vehicle after the application of brake, termed as Braking Distance(\(L_B\)).
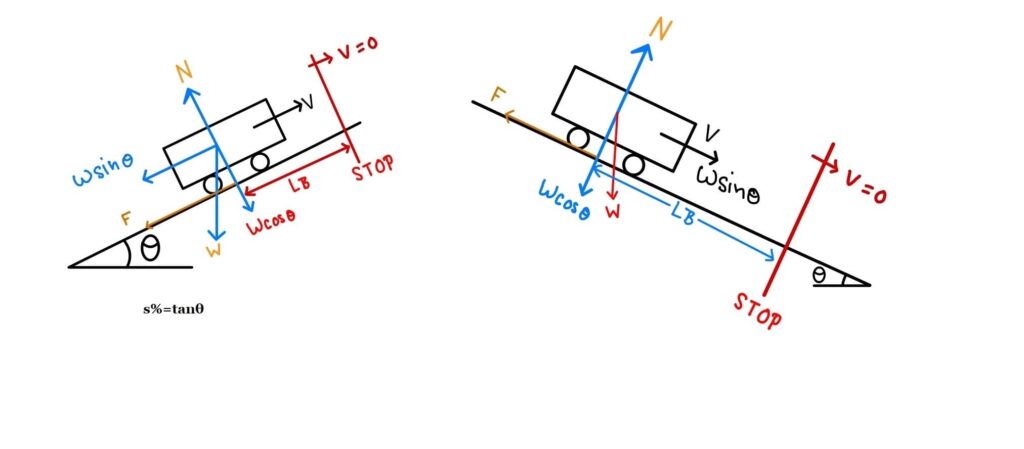
Case-1: Ascending Gradient:→
Gradient= tanθ= \(\frac{s}{100}\)= s%
Total Resisting Force= mg·sinθ+ F | |
F= Friction Force F= Normal Force×Friction Coefficient. F= f×mg·cosθ | |
Total Resisting Force= mg·sinθ+f×mg·cosθ | |
Equating the kinetic energy of vehicle and work done to stop it.
ΔK·E= Work Done (Work Done= Force× Distance)
Case-2: Decending Gradient:→
\(L_B\)=\(\frac{V^{2}}{254(f-s \%)}\)
Case-3: Flat Road:→
s=0 |
SSD=\(L_L+L_B\)
SSD=\(0.278\times V\times tr\)+ \(\frac{V^{2}}{254(f±s \%)}\)
SSD= Stopping Sight Distance (meter)
V= Design Speed(m/sec)
tr= Reaction time(sec)
f= Friction Coefficient(unit less)
s= Gradient
Note:
- SSD must be available at each & every section of the road.
- As the SSD, required on descending gradient is higher, it is necessary to determine the critical value of SSD for the descending gradient on the roads with gradient & for two way traffic flow.
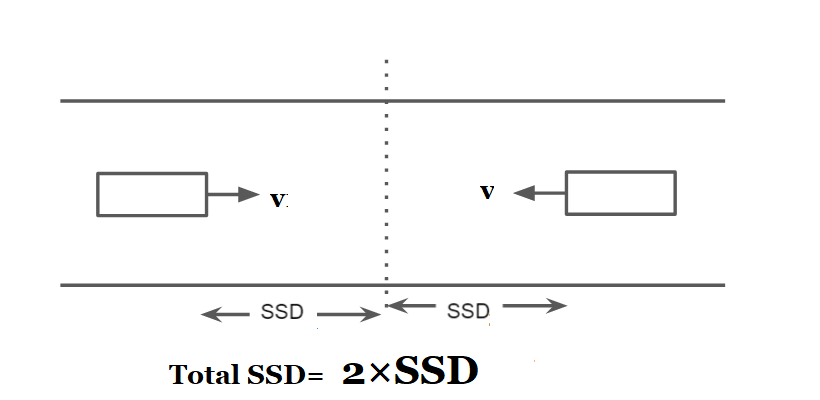
- On the restricted width or on single lane roads when two way movement of traffic is permitted, the minimum SSD equal to twice the SSD to enable both the vehicle coming from opposite side to stop.(For single lane road,two way traffic)
- If SSD can not be provided on any stretch of road due to unavoidable reason for the design speed available, the speed should be restricted either by installing speed- limit regulation signs or by forced reduction of the speed.
- This is however temporary, and efforts must be made to provide SSD over the period of time. (By the changing alignment of road or by removing the obstruction.)
- The SSD recommended by IRC are as follows:

For Detailed Analysis of Highway Engineering Step By Step.