Relative Compaction | Properties of Soil | Soil Mechanics

  Relative Compaction (Rc)  

It is used to indicate the degree of denseness/compactness in absolute terms as density index (ID), but it can be applied for both cohesionless & cohesive soil.

\(\mathrm{Rc}=\frac{\gamma_{d}}{\gamma_{\text {dmax }}} \times 100\)

Relative Compaction is unit less.

It is defined as the ratio of the dry unit weight of soil in the existing/natural state to the dry unit weight of soil in the densest state.

\(\gamma_{d}\)= Dry unit weight of soil in existing / natural state.

\(\gamma_{dmax}\)= Dry unit weight of soil in densest state.

\(\begin{array}{l}
\mathrm{Rc}=\frac{G \gamma_{w}\left(1+e_{\min }\right)}{(1+e) G_{\psi}} \times 100 \\
\mathrm{Rc}=\frac{\left(1+e_{\min }\right)}{(1+e)} \times 100
\end{array}\)

Rc= 80 + 0.2ID

In loosest state ⇒ Id=0% ⇒ Rc⇒ 80%.

In densest state ⇒ Id=100% ⇒ Rc⇒ 100%. 

---

Calculate the value of (e)max, (e)min, (η)max, and (η)min

  Packing of Uniform Sphere  

• Packing of the uniform sphere is the only system, void ratio of porosity of which can be found mathematically.
• Spheres of uniform size attain stable loosest packing in a “cubical array“.
• Spheres of uniform size attain stable densest packing in “Rhombohedral array“.

1. Loosest State 

Here each particle is in contact with 6 more similar particles.

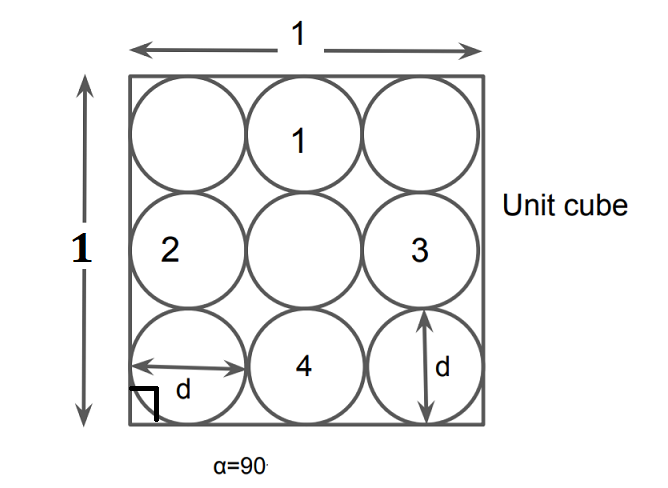
Volume of soil V=1*1*1  = 1m³.

Volume of solids in soil = (1/d)*(1/d)*(1/d) = 1/d³

The volume of one solid = πd³/6.

Total volume of solids Vs = \(\frac{\pi d^{3}}{6} \times \frac{1}{d^{3}}=\frac{\pi}{6}\)

Volume of voids Vv= V-Vs=1-(π/6)=0.476m³.

\(e_{\max }\)= Vv/Vs. = .476/(π/6) =.91

\(η_{\max }\)= \(e_{\max }\)/(1+\(e_{\max }\)) = .91/(1+.91) =.47

---

2. Densest  State 

Here each particle is in contact with 12 more similar particles.

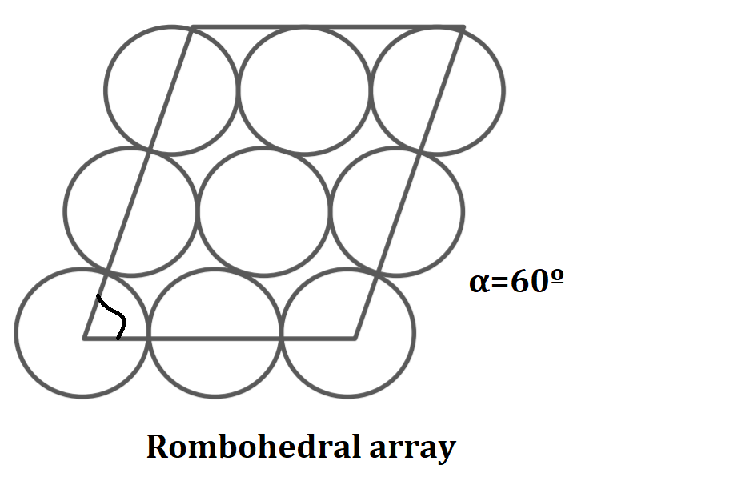
Volume of unit rhombohedral

V=\(\sqrt{1+2 \cos \alpha} \times(1-\cos \alpha)\)

Volume of soil α=60º

V=\(\sqrt{1+2 \cos60º } \times(1-\cos60º)\)=0.707m³

Volume of solids Vs = π/6.

Volume of voids Vv= V-Vs= 0.707-(π/6)=0.183m³.

\(e_{\min }\)= Vv/Vs. = .183/(π/6) =.35

\(η_{\min }\)= \(e_{\min }\)/(1+\(e_{\min }\)) = .35/(1+.35) =.26

---

If \(e_{\min }\),\(e_{\max }\) is not given in Question, then apply

\(e_{\min }\)=0.35,

\(e_{\min }\)=0.91.

---

Subject	Soil Mechanics
Unit	Soil Formation & Properties of Soil
Topic	Relative Compaction
Next Topic	Interrelationship Between the Properties of Soil
Previous Topic	Density Index

---