Levelling
It is the method of determining the difference of elevation or level of different points on earth’s surface. If all the heights of different points are measured related to a plane, the plane is termed a datum plane. In general this datum plan is taken to be mean sea level (MSL), to standardize the measured to height Internationally.
Important Terminologies In Levelling
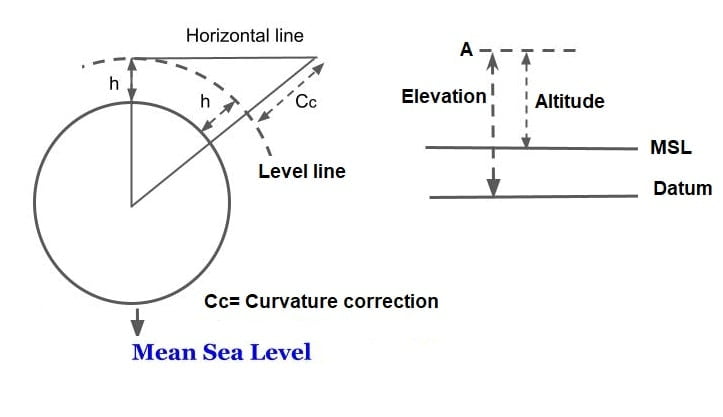
Elevation & Altitude
- If the vertical distance of the point is above or below the datum surface is noted as Elevation.
- It is the vertical distance of a point above MSL i.e when datum is MSL, the elevation is termed as Altitude.
Note- If the datum surface is MSL then elevation is the same as attitude.
Reduced Level
Elevation of a point with respect to mean sea level is called reduced levels. And the process of determining the difference in reduced level of the point is called and levelling.
Mean Sea Level
It is the mean data of sea fluctuation considered at Mumbai. It is used as datum/reference to find reduced levels. The value of mean sea level as a datum is obtained by averaging the elevation of high and low tides, at several points for a long period of time about 19 years.
Bench Marks(B.M)
The benchmark is a fixed point of known elevation above the datum. Any point whose elevation is definitely known can be used as a bench mark.
The following type of bench marks are established and used.
1.G.T.S Bench Marks
The great trigonometrical survey (G.T.S) bench marks are those which are established by the survey of India which very high accuracy throughout the country.
2.Permanent Bench Marks
The permanent benchmark are those which are established on a permanent structure. These bench marks are established by PWD or survey of India.
3.Temporary Bench Marks
These are the bench marks established temporarily whenever required.
4.Arbitrary Bench Marks
These are the bench marks whose elevation are arbitrary assumed for levelling of a small area.
Measurement in Leveling Work
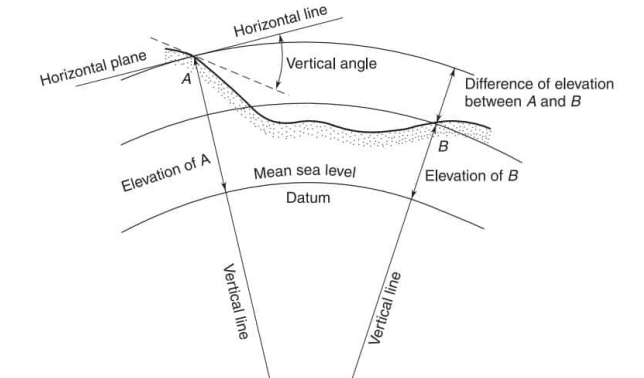
Horizontal Line
Line setup by an instrument keeping the bubble at centre is called horizontal line. This line is always tangent to the earth surface.
Vertical Line
It is a line from any point on the earth’s surface to the center of earth. Ex- Plumb line.
Level Line
It is an imaginary line considered to parallel M.S.L. Level line perpendicular to the plumb line.
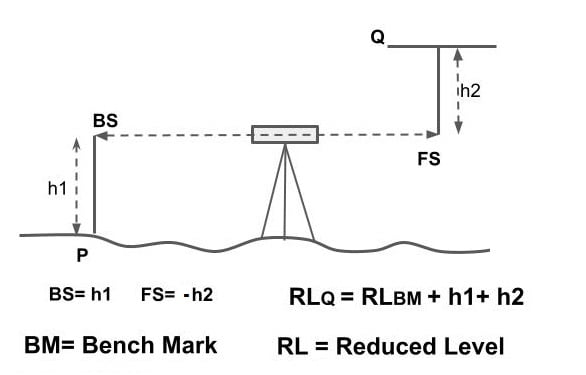
Back Sight Reading
On first reading taken from instrument position are called back sight reading. It is always taken to benchmark.
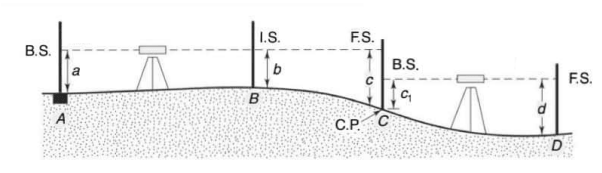
Fore Sight Reading
The last reading taken from instrument position are called fore sight reading. After fore sight reading either instrument is shifting or the work is closed.
Intermediate Sight Reading
All other reading except back sight & fore sight are called intermediate sight reading.
Method to Find Reduced Level
Assumption
- Survey is Plane
- Effect of earth curvature is not considered.
For computation of reduced level of various point, two method are used:
- Height of Instrument
- Rise and Fall method
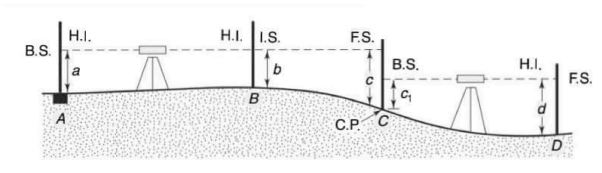
Height of Instrument
The first reading is always back sight.
The last reading is alway fore sight.
HI= RL of BM + BS
RL at any point= HI – Staff Reading
ΣBS- ΣFS = Last RL – First RL
Rise and Fall Method
RL of any point= RL of previous point + Rise(-Fall).
ΣRise – ΣFall = Last RL- First RL.
ΣRise – ΣFall = Last RL- First RL = ΣBS- ΣFS
Inverted Staff
Some time leveling staff is inverted in levelling work to find the Reduced level of ceiling, arches, beam etc.
Inverted staff readings are represented with -ve sign.
Correction Required in Levelling Work
1.Correction due to Earth Curvature (Cc)
Staff reading should be taken corresponding to levelling but it is found corresponding horizontal line.
Net difference between horizontal line and level line is called correction due to earth curvature.
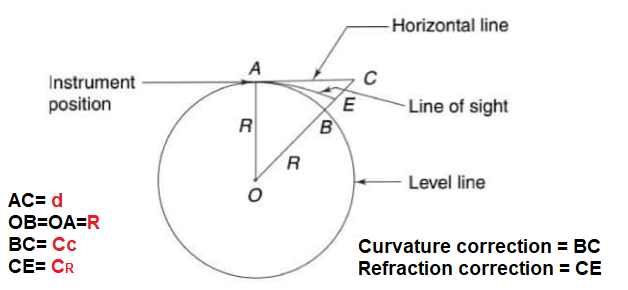
(R+Cc)2 = R2 + d2
R2+Cc2 + 2·R·Cc = R2 + d2
| Cc (Cc + 2·R) = d2 | Cc<<< 2R, so: Cc+2R≈ 2R |
Cc (2·R) = d2
\(Cc=\frac{d^{2}}{2R}\) {Cc→km, d2→km2, R→km}
This correction is always (-ve) negative.
\(Cc=\frac{d^{2}}{2\times 6370}\times 1000\).
\(Cc=-0.0785d^{2}\)
Cc in meter, d in Kilometer
2.Correction due to Refraction (CR)
Due to the effect of refraction line of sight is shifted in downward direction due to which lesser reading is obtained in staff hence this correction is always +ve in nature.
Magnitude of this correction is taken as 1/7 of correction due to earth curvature.
CR= +0.0112d2.
CR in meter, d in Kilometer
3.Combined Correction due to Both (C)
C= Cc + CR
C= Cc + CR
C= -0.0785d2 + 0.0112d2
C= -0.0673d2
C in meter, d in Kilometer
| Note | In staff reading = h Correct staff reading = h-0.0673d2 |
Distance of Visible Horizon
Maximum distance visible from any height is called distance of visible horizon.
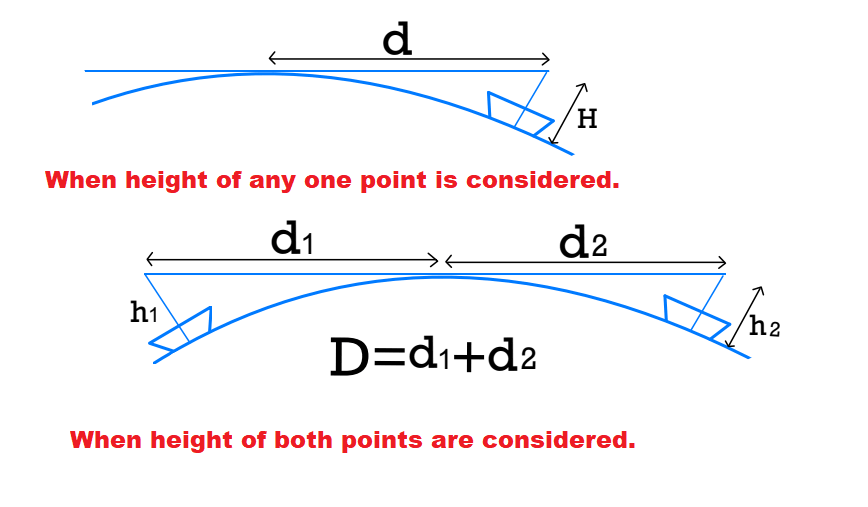
Case.1 When height of any one point is considered.
H= C= 0.0673d2
Distance of visible horizon \(d=\sqrt{\frac{H}{0.0673}}=3.855\sqrt{H}\)
| \(d= 3.855\sqrt{H}\) | d→km, H→m |
Case.2 When height of both points are considered.
D = d1+d2
Distance of visible horizon \(d= 3.855\left ( \sqrt{h_1}+ \sqrt{h_2} \right )\)
| d→km, h1→m, h2→m |
Reciprocal Leveling
This technique of leveling work is used to find the exact height difference between two points on the opposite banks of a river or a deep gorge.
By Reciprocal leveling
- Effect of curvature, Refraction & collimation ( Collimation means bubble in center but not horizontal) are eliminated.
- Collimation error can be found.
Procedure
To point A,B are selected on opposite site of obstruction and staff reading taken the both station keeping the instrument first near station A and then near station B.
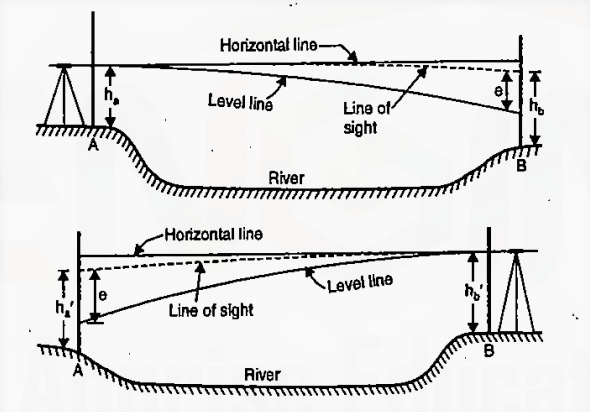
Case.1 When the instrument near A
Staff reading at A = hA
Staff reading at B = hB
error e in the staff reading on B
Corrected staff reading B= hB-e
Height different between A & B
H= (hB- e)- hA —(1)
e= error due to curvature, collimation, refraction.
Case.2 When the instrument near B
Staff reading at A = hA’
Staff reading at B = hB’
error e in the staff reading on A
Corrected staff reading A= hA’ – e
Height different between A & B
H= hB‘ – (hA‘-e) —(2)
From equation 1 & 2
H= (hB – e) – hA —(1)
H= hB’- (hA’- e) —(2)
Equation 1+2
2H= (hB-hA) + (hB’-hA’)
Exact height difference H
H= \(\frac{(hB-hA) + ({hB}’-{hA}’)}{2}\)
RLB = RLA– H. RLB = Reduced level of B | RLA = Reduced level of A H = height difference between A & B |
Collimation error
It is a type of instrumental error due to which the line of Collimation is not horizontal even if the bubble is at centre.
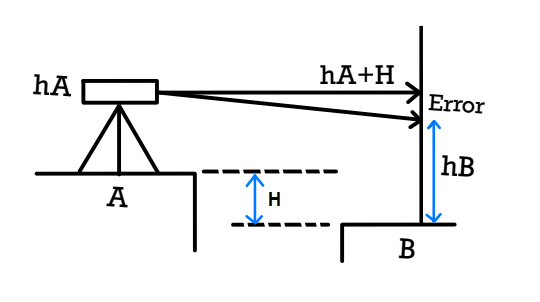
Measured staff reading at B= hB
True staff Reading at B should be = hA+ H
Error = E= hB – (hA+H).
Case.1 When Area is Large
Error= ECURVATURE + EREFRACTION + ECOLLIMATION
| Ec+ ER + Ecl = hB- (hA+H) | Ec= -0.0112d2 ER= +0.0785d2 |
Case.2 When Area is small
Effect of curvature & refraction are neglected
| Ec+ ER + Ecl= hB- (hA+H) | Ec →0, ER →0 |
Ecl = hB- (hA+H)
If Ecl is -ve then Light of sight shifts in downward direction.
If Ecl is +ve then Light of sight shifts in upward direction.
Angular / Inclination Error
\(\theta = tan^{-1}\left ( \frac{E_{\text{cl}}}{d} \right )\)
Sensitivity of Bubble Tube
Angle of rotation given to the telescope due to just one division movement of the bubble inside the bubble tube is called sensitivity. Activeness of bubbles is called sensitivity. The sensitivity is expressed as second/division. If not mentioned the length of the division should be taken as 2 mm.
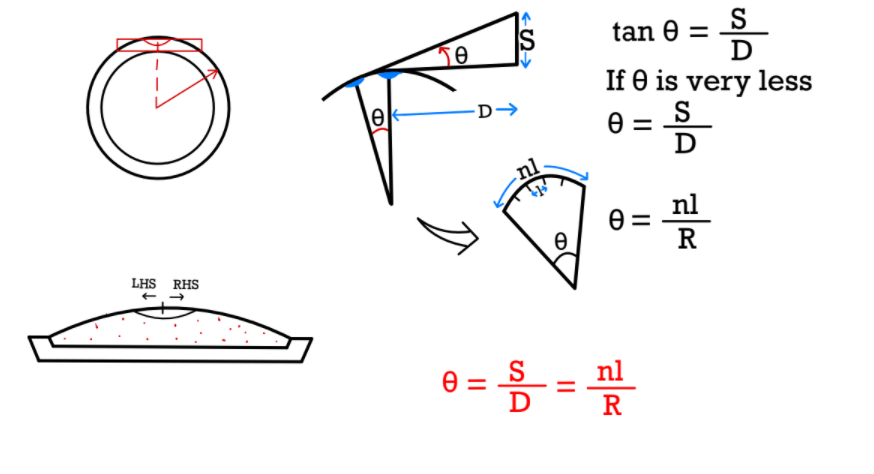
Sensitivity
\(\alpha =\frac{\theta }{n}\).
\(\alpha =\frac{l }{R}=\frac{S}{nD}\) Radian.
π Rad= 180°
1 rad= \(\frac{180° }{π}×60×60\) = 206265 second.
Sensitivity
\(\alpha =\frac{l}{R}×206265 \) second.
\(\alpha =\frac{S}{nD}×206265\) second.
l= length of one division of bubble tube
R= radius of curvature of bubble tube
S= staff intercept (different b/w staff reading)
D= Distance from instrument to staff
n= number of division
Thankyou sir,
Aapke in notes se kaafi help hui h SURVEYING complete krne m.
Please mere request h ki jlde se aap baki importank subjects b complete krde.
Thankingyou