Traverse Survey  

It is the process of measuring the length and direction of a survey line (traverse line) in the field. A traverse is a series of connected lines whose length and direction are being measured in the field. The field work in theodolite traverse includes.

• Reconnaissance 
• Selection and marking of survey stations
• Running and measuring traverse line
• Angular measurements and marking the offsets

  Types of Traverse 

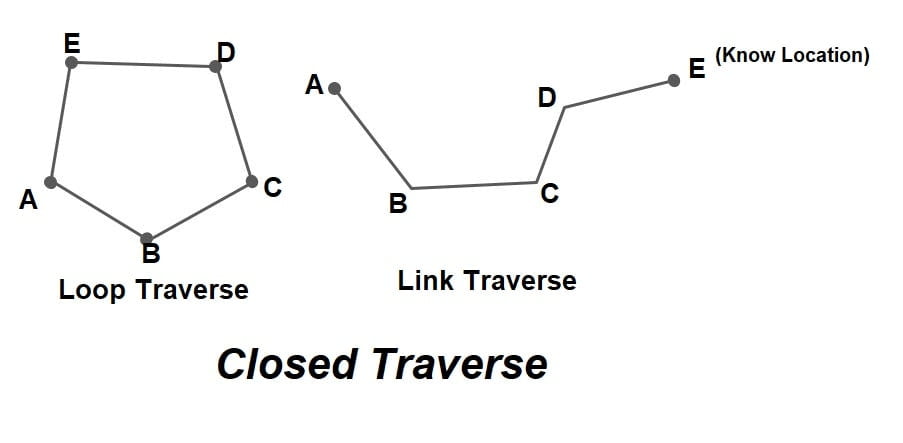
A). Closed Traverse 

1. A closed traverse starts from a station and closes either on the same station or another station whose location is already known.
2. If a traverse starts and ends at the same point whose location is known this type of closed traverse is termed as loop traverse.
3. If a traverse starts and ends at different points of known location, this type of closed traverse is termed as link traverse.
4. In cased closed traverse, it is easy to detect the error and adjust or balance it.

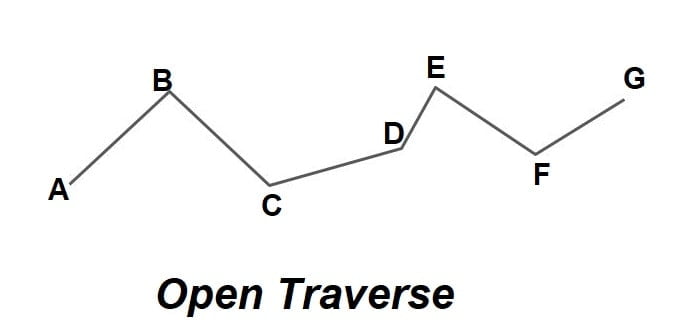
B). Open Traverse

1. An open traverse is that where the start station is known or established, but the station at which the traverse is complete/closes is not known or established.
2. It is used for the survey of roads, railways, canals, tunnels etc.
3. An open traverse cannot be properly checked and adjusted or balanced hence it is avoided.

  Method of Traversing  

1.  Linear measurement 
2. Angular measurement

1. Linear Measurement 

The method of linear measurement adopted depends upon accuracy required in fieldwork. The degree of accuracy obtained in both linear and angular measurement must be the same.

Example:

If the compass has a least count of 30’ (30 minute), the linear measurement must be done with a permissible error or not more than 1 in 150.

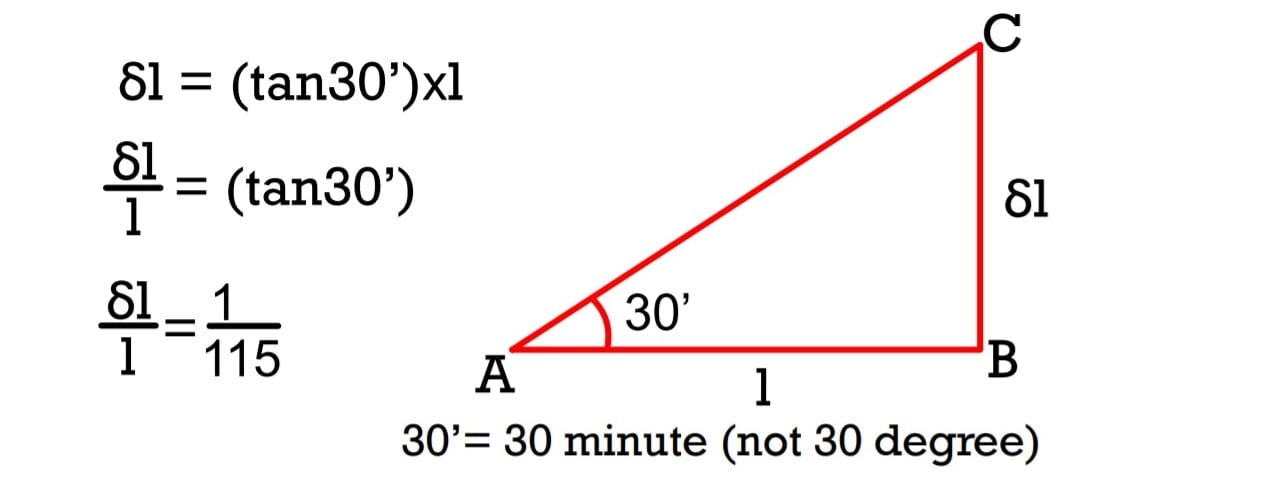
Note: If theta is small, θ≅ tanθ, then for consistent precision in angular & linear measurement.

\(δθ= \frac{δl}{l}\)

Linear measurement can be done by 

• Chaining or Taping
• Tacheometric Method
• EDMI (Electronic Distance Measurement Instruments)

2. Angular Measurements

1. Loose needle method of bearings
2. Fast needle method of bearings
3. Method of included angles
4. Method of direct angles
5. Method of deflection angles

A. Loose Needle Method

In this method  direction of the magnetic meridian is established at each traverse station and the direction of the line is measured with reference to the magnetic meridian. In other words, the magnetic bearing of each line is measured at each station. A theodolite fitted with a magnetic compass is used for measuring the magnetic bearings of the traverse line. It is also known as the free needle method.

B. Fast Needle Method

In the fast needle method, the magnetic meridian is established only at the starting station and the magnetic bearing of the first line is measured.The magnetic bearings of remaining traverse lines are determined indirectly from the magnetic bearing of the first line and the included angles.However the magnetic bearing of the first line has the accuracy of the compass, the difference. of bearings of the two adjacent lines has the accuracy of the theodolite.The method is more accurate than the loose needle method, and is generally preferred in the field

C. Method of Included Angle

 It is the most commonly used method of traversing. In this method, Magnetic bearing of the initial line is measured. Bearing of all the remaining lines is determined from the bearing of the initial line and the included lines. All angles measured clockwise.

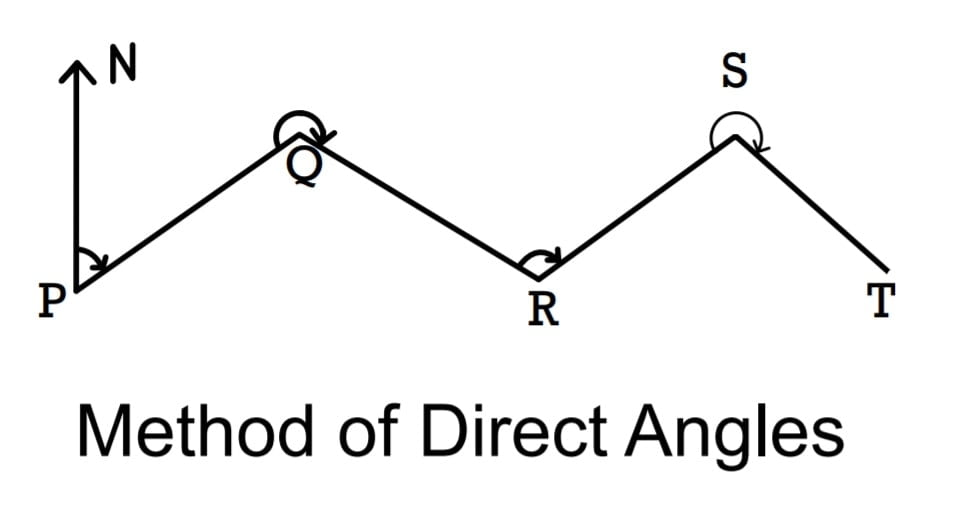
D. Method of Direct Angles

Direct angles method is similar to the method of included angles. This is suitable to be used for open traverse.

E. Method of Deflection Angles

Method of deflection angles is also used for open traverse. Deflection angle is defined as an angle which a line makes with the prolongation of the previous line.

Note: 

• Once the traversing is complete , check must be applied over the measured interior angles.
• If the sum of the major interior angle is not equal to the theoretical sum {(2N-4)x 90°}, the angle misclosure is attained. ( Angle Misclosure is equal to the difference between the actual sum of the major angle and the theoretical sum of included angles.)

Balancing the Angle of Traverse

The angle of close traverse is balanced or adjusted such that they satisfy the required condition of the geometrical figure.

Average Correction Method

In this method, a uniform average correction is applied to all the angles.

Consider a closed traverse ABCDE having 5 sides in which the included angles measured are as below:

We know that

Theoretical sum=(2N-4) x 90° = (2x 5-4) × 90°=540°

Angular misclosure = 540°01’00”- 540°⇒  1′ = +60″

Correction per angle = -60″/5= -12″

The corrected values of the angles A, B, C, D and E are 101° 14’8″; 230 54’8″; 16° 41′ 48″; 89° 35′ 8” and 101° 34′ 48” respectively.

  Latitude And Departure  

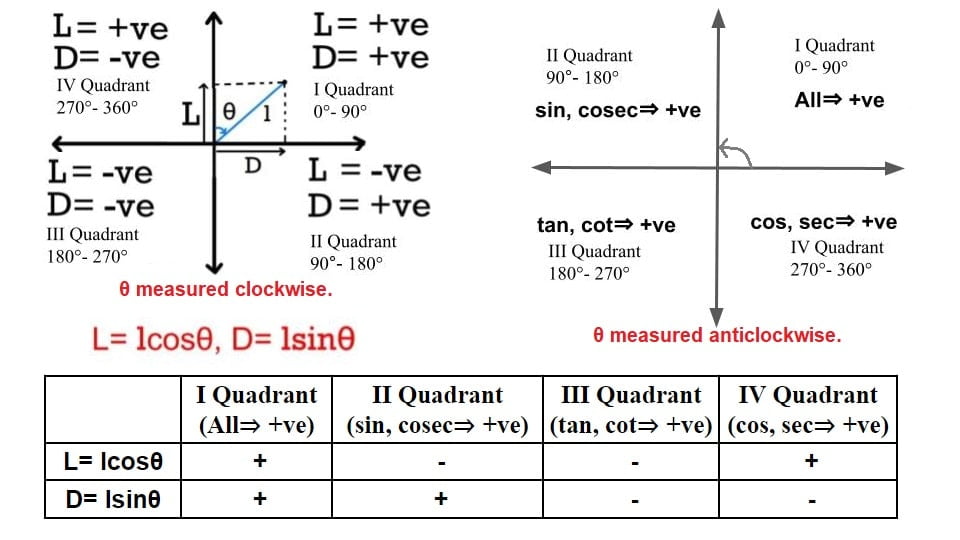
Latitude (L)

Projection of a line on the north & south axis is called latitude. It is considered positive on the north axis and negative on the south axis also known as northing and southing respectively.

Departure (D)

Projection of a line on the east & west axis is called departure. It is considered positive on the east axis and negative on the west axis also known as easting and westing respectively.

Note

• Latitude and departure is always calculated using the fore bearing of a line.
• For calculation of latitude and departure, if bearing θ is taken in the whole circle bearing & the nature of latitude and departure will be taken  can be lcosθ , lsinθ, respectively.
• If latitude and departure are computed with the help of quadrantal bearing, respective signs are to be applied over it.

  Checks in a Closed Traverse  

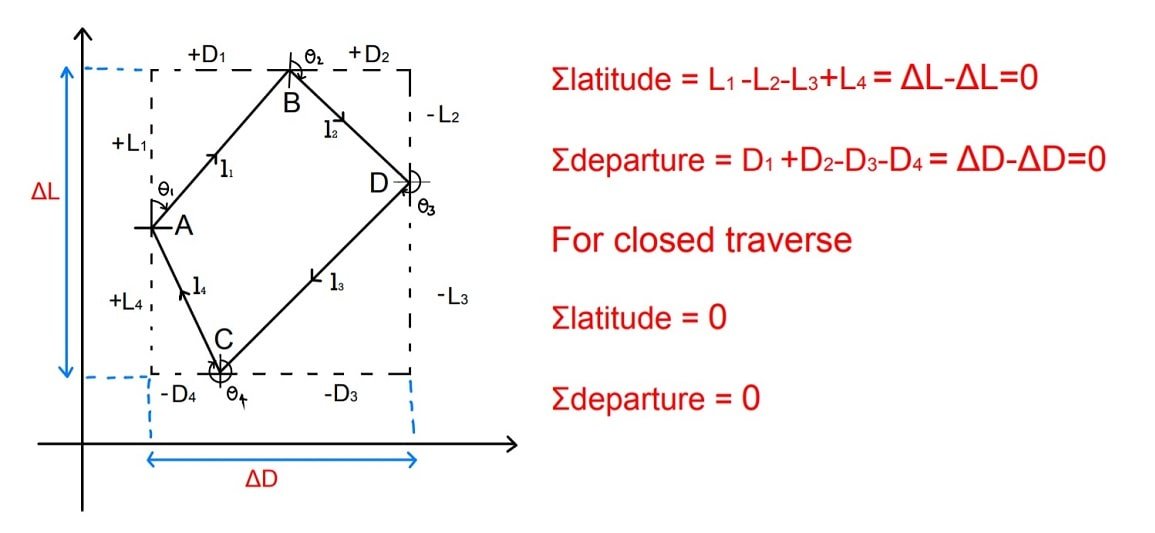
Loop Traverse

In a closed loop traverse, the following two conditions should be satisfied. 

Case 1. The algebraic sum of all the latitudes should be equal to zero.

ΣL = L1 + L2 + ……=0

In other words, the arithmetic sum of northings should be equal to the arithmetic sum of southings.

Case 2. The algebraic sum of all the departures should be equal to zero.

ΣD = D1 + D₂+ ……= 0. 

In other words, the arithmetic sum of eastings should be equal to the arithmetic sum of westings.

Link Traverse

In case of a link traverse, the following two conditions should be satisfied.

Case 1. The algebraic sum of all latitudes should be equal to the difference in the latitudes of the final control point and the initial control point.

ΣL = L1 +L₂ + ….. = Latitude of the final control point- latitude of the initial control point

Case 2. The algebraic sum of all departures should be equal to the difference in the departures of the final control point and the initial control point.

ΣD = D1 + D2 +…… = Departure of the final control point-Departure of the initial control point.

  Closing Error  

After completing a closed traverse survey at the time of plotting. The traverse is not getting closed than a closing error found. (Σlatitude ≠0,  Σdeparture ≠0)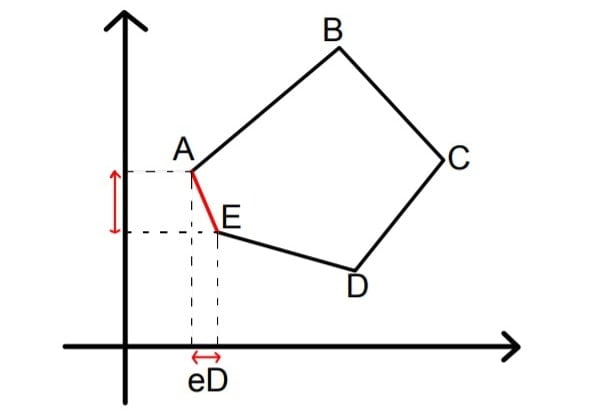

eL= Σlatitude = total error in latitude (≠0)   

ed= Σdeparture = total error in departure (≠0)

  Relative Error of Closure or Relative Precision  

Relative error of closure = \(\frac{\text{Error of closure}}{\text{Perimater of traverse}}\)

Relative error of closure = \(\frac{e}{p}\)

Generally relative error of closure is expressed as (\(\frac{e}{p}\)). Relative Error of Closure or Relative Precision is also called relative accuracy or degree of accuracy.

  Method to Correct Clothing Error  

Bowditch’s Rule

• Bowditch’s Rule is also called the compass rule.
• This method is used when linear measurement and angular measurement both take equal degree of precision.

Assumption 

Error in linear measurement is directly proportional to \(\sqrt{L}\) = α\(\sqrt{L}\)

Error in angular measurement is inversely proportional to \(\sqrt{L}\) = α\(\frac{1}{\sqrt{L}}\)

Error 

•  According to this method error is distributed as for the ratio of length of different lines.

Let 

l1, l2, l3, ……ln ⇒ Length of different line.

ΣL = (l1 +l2 +l3…..+ln)⇒ Perimeter of traverse 

eL⇒ Total error in latitude.

eD⇒ Total error in departure.

Correction for latitude of a line CL1= \(-\frac{l_1}{Σl}×eL\)

Corrected latitude =L1+ CL1

Correction for depature of a line CD1= \(-\frac{d_1}{Σd}×eD\)

Corrected departure =D1+ CD1

Transit Rule

This method is used when angular measurement is more precise than linear measurement.

Let 

L1, L2, L3,…….Ln.  are the latitude of different line.

 D1, D2, D3,……Dn. are the departure of different line.

L_T =Sum of magnitude of all latitude.

D_T =Sum of magnitude of all departure.

eL⇒ Total error in latitude.

eD⇒ Total error in departure.

Correction for latitude of a line CL1= \(-\frac{|L_1|}{L_T}×eL\)

Corrected latitude =L1+ CL1

Correction for depature of a line CD1= \(-\frac{|D_1|}{D_t}×eD\)

Corrected departure =D1+ CD1

Note

• When the Traverse is adjusted by Bowditch’s rule, both the length and bearing of the lines are changed. however in comparison to transit rule the lengths are changed less and the angles are changed more.
• If a line has zero latitude (or departure), there will be no correction to the latitude ( or departure).

FOR MORE INFORMATION ABOUT SURVEYING