Superelevation:

The transverse inclination throughout the length of horizontal curve by raising outer edge counteract w.r.t. inner edge, in order to counteract the effect of centrifugal force is known as superelevation (or cant or banking).

Note: This topic is part of the second chapter of Highway Engineering. I suggest reading this topic in the context of the complete chapter: Geometric Design of Highway. If you want to read the entire Highway Engineering, click here: Highway Engineering.

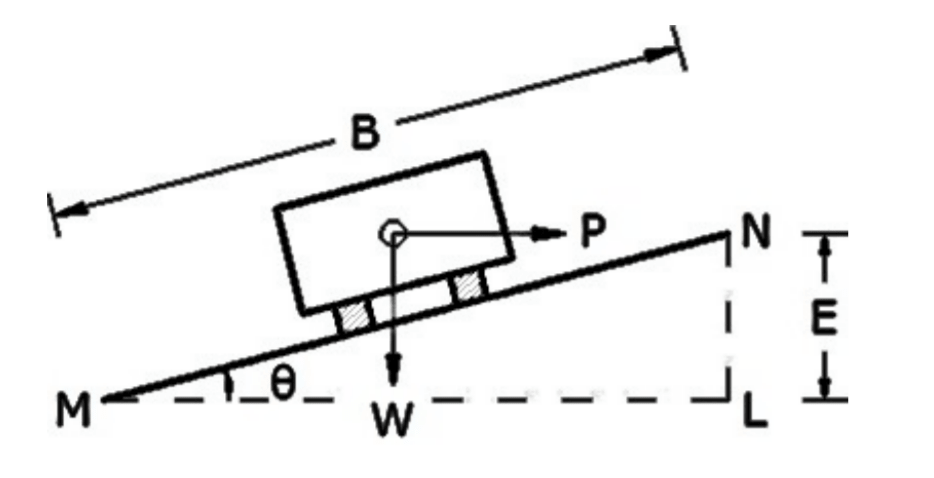
The superelevation ‘e’ is expressed as the ratio of height of outer edge w.r.t. the horizontal width, i.e

Superelevation (e)= \(\frac{NL}{ML}\)

e= tanθ

θ is very small and the value of tanθ ⊁ 0.007 (7%)

e= tanθ ≅ sinθ = \(\frac{E}{B}\)

Analysis for Expression of Super-elevation

Consider a vehicle moving at a speed of v m/s on a circular curve having radius ‘R’.

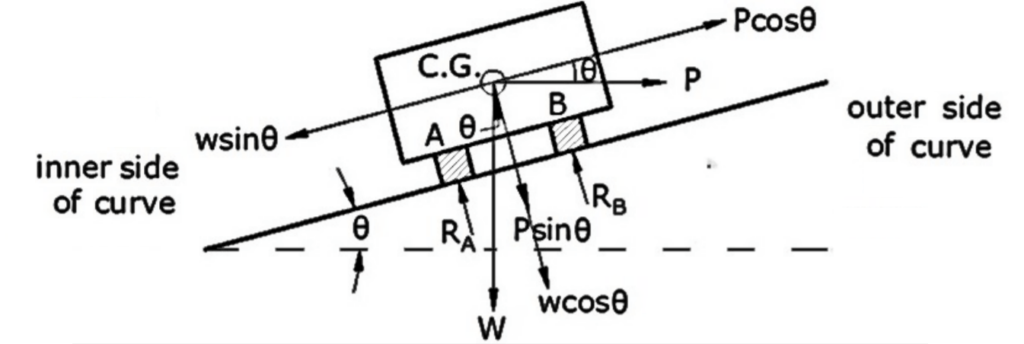
The following forces acting on the vehicle:
i) Centrifugal force (P) acting horizontally through the center of gravity (CG) of vehicle

P= \(\frac{mv²}{R}=\frac{W·v^{2}}{gR}\) ——-(1)

ii) The weight (W) of the vehicle action vertically downwards through the C.G. of the vehicle
iii) The frictional force (FA & FB) developed between the wheels and pavement, transversely along the pavement surface.

F_A =R_A ×f and F_B =R_B ×f ——-(2)

where

R_A and R_B = frictional resistance between wheel and pavement
f = coefficient of lateral friction

Considering equilibrium, the component of centrifugal force parallel to the pavement (Pcosθ) is opposed by component of weight parallel to the pavement and frictional force F_A and F_B,

P cosθ= W sinθ + (F_A + F_B )

P cosθ= W sinθ + f(R_A + R_B )

P cosθ= W sinθ + f(P sinθ+ W cosθ )

P(cosθ- sinθ)= W(sinθ +fcosθ)

\(\frac{\mathrm{P}}{\mathrm{W}}=\frac{\sin \theta+f \cos \theta}{\cos \theta-f \sin \theta}\)

dividing by cosθ on right side term

\(\frac{\mathrm{P}}{\mathrm{W}}=\frac{\tan \theta+f }{1-f \tan \theta}\).

from equation 1              \(\frac{P}{W}=\frac{v^{2}}{gR}\).

\(\frac{v^{2}}{gR}=\frac{tan\theta +f}{1-ftan\theta}\).

\(\frac{v^{2}}{gR}=\frac{e+f}{1-ef}\).

Here, Coefficient of lateral friction ( f ) = 0.15

Maximum value of super-elevation (tanθ) = 0.07 (7 %)

1-e·f= 0.99≅ 1 (As per IRC)

hence

e+f=\(\frac{v^{2}}{gR}\)    , v in m/sec

Here, e = rate of super-elevation = tanθ
If the speed of vehicle is represented as V kmph then

Formula for Superelevation

e+f=\(\frac{V^{2}}{127R}\)    , V in km/h

Note: For Racing Track

\(\frac{e+f}{1-ef}= \frac{v^{2}}{Rg}\), v in m/sec