Stability Analysis on Horizontal Curve without Superelevation:

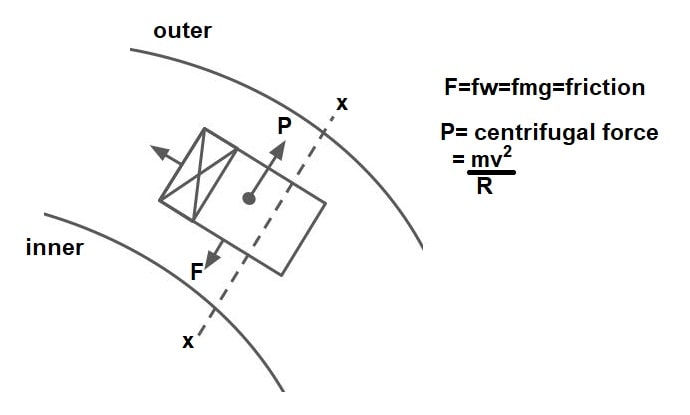
It is the curve in plane to provide change in the direction to Central line on the road. When a vehicle travel on a horizontal curve, the centrifugal force act horizontally outward through the center of gravity of the vehicle.

Note: This topic is part of the second chapter of Highway Engineering. I suggest reading this topic in the context of the complete chapter: Geometric Design of Highway. If you want to read the entire Highway Engineering, click here: Highway Engineering.

The centrifugal force depends upon the speed of vehicle and the radius of horizontal curve.

It will be counteracted by lateral /transverse friction developed between the tyre & pavement, which helps the vehicle to change direction along the curve.

        They are the centrifugal force (P) acting outward, weight of the vehicle (W) acting downward, and the reaction of the ground on the wheels (RA and RB). The centrifugal force P in Newton is given by

         \(P=\frac{mv^{2}}{R}\)

        where m is the mass of the vehicle in kg, v is the speed of the vehicle in m/sec, g is the acceleration due to gravity in m/sec2 and R is the radius of the curve in m. The centrifugal ratio or the impact factor \(\frac{P}{W}\) is given by:

\(\frac{P}{W}=\frac{\frac{mv^{2}}{R}}{mg}=\frac{v^{2}}{gR}\)

        The force acting on vehicle has the tendency to either overturning the vehicle outward about wheels & to skid the vehicle laterally outward.

1. Overturning the vehicle

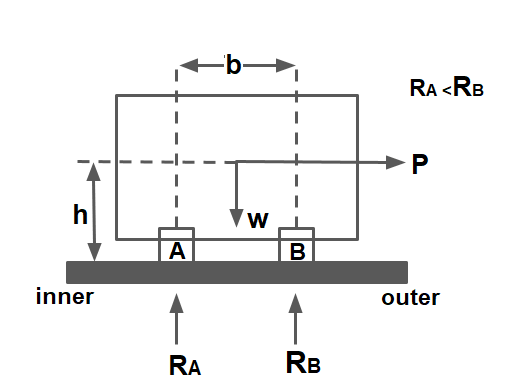
M_O= P×h= Overturning  Moment

M_R= W×(b/2)= Resistive  Moment

Case.1 To avoid overturning:

M_O < M_R

P×h< W×(b/2)

I= \(\frac{P}{W}<\frac{b}{2h}\)

Case.2 On the verge of overturning:

M_O = M_R

P×h= W×(b/2)

I= \(\frac{P}{W}=\frac{b}{2h}\)

Case.3 Unsafe case:

M_O > M_R

P×h> W×(b/2)

I= \(\frac{P}{W}>\frac{b}{2h}\)

2. Lateral skiding of the vehicle

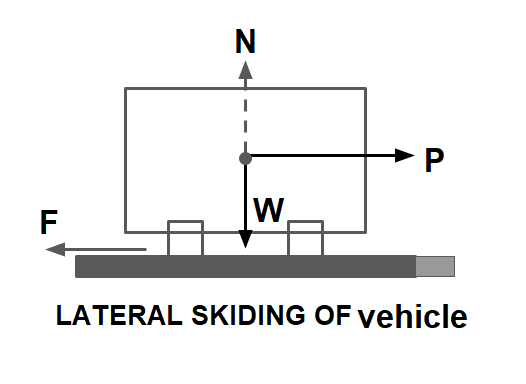
Skiding Force= P= \(\frac{mv²}{R}\)

Resistive Force= F= f·W= f·m·g

Case.1 To avoid skiding:

P< f×W

I= \(\frac{P}{W}<f\)

Case.2 On the verge of skiding:

P= f×W

I= \(\frac{P}{W}=f\)

Case.3 Unsafe case:

P> f×W

I= \(\frac{P}{W}>f\)

Note:

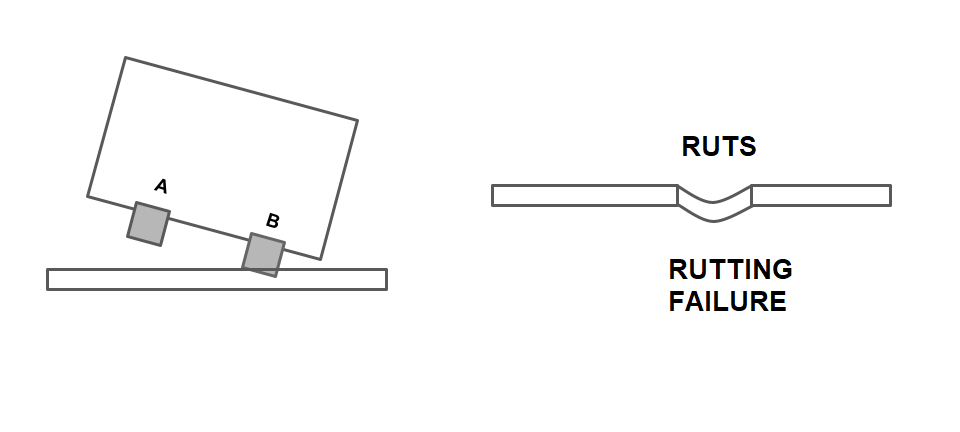
• If pavement is kept horizontal across the alignment, The pressure on the outer will be higher due to centrifugal force acting outward direction.
• When the limiting equilibrium condition for overturning occurs, the pressure at inner wheel becomes zero.
• Since pressure on outer wheel is comparatively more, it damages the pavement by developing ruts over it. RUTTING FAILURE

• Hence to avoid both overturning & sliding :

\(I=\frac{P}{W} \leq\left\{\begin{array}{c}
\frac{b}{2 h} \\
and \\
f
\end{array}\right.\)

• The relative dangerous of lateral skidding and overturning depends upon weather ‘f’ is lower or higher than \(\frac{b}{2h}\).
• If

f< \(\frac{b}{2h}\)⇒ Transverse of skidding before overturning.

f> \(\frac{b}{2h}\)⇒ Overturning before transverse skidding.

For Detailed Analysis of Highway Engineering Step By Step.

Highway Engineering