Linear Measurement
To measure the distance between two points on a horizontal plane along the straight line & to rotate the different position on ground in terms of linear measurement. Linear measurement can be obtained by chain surveying in which chain or tape is used. The main purpose of survey is to plot the map of the area. Map is plotted on a horizontal plane and thus distances shown in the map are horizontal projections.It is suitable for small, open area having few simple details.
Procedure in Chain Surveying
Chain surveying consists of measuring the length of a series of straight lines with tape/chain and then locating the details on the ground relative to these lines. The details are located by measuring two other lines termed as ties or by measuring offsets.

Basic Definition of Chain Surveying

Main Station
Main station is a point in the chain survey where the two sides of the triangle meet. These stations command the boundaries of the survey. Here A,B,C,D are the main stations.
Tie Station
It is the point on the line joining two Main Station. It is used for locating interior details of an area. Ex: e,f,g,h,i
Main Survey Line
The chain line joining two main survey stations is called main survey line. AD, DB, BC, CA, main survey lines.
Tie Line/ Subsidiary Line
It is the line joining the two tie stations. The line are provided to locate the interior details which are far away from the main survey lines. Ex: ef,gh.
Base Line
Longest line in a chain survey which will divide the whole area into two parts is called the base line. Ex: AB.
Check Line/ Proof Line
Any line used to check accuracy of survey work is called a check line. Ex: Cg,Di.
Offset
It is the distance of an object from the survey line.It may be perpendicular or oblique.
Chainage
It is the distance measured along the main survey line in the direction of progress of work. It is generally used in linear construction projects. Example : Road, railway, sewer, water pipeline.
Well Conditioned Triangle
In chain surveying efforts should be made to select main survey stations such that they form a “well conditioned triangle”. It is a triangle if all intersections of lines are clear for plotting purposes. If the angle between the lines are between 30° to 120°, clear intersection or achieve. An equilateral triangle will be the most appropriate well conditioned triangle.
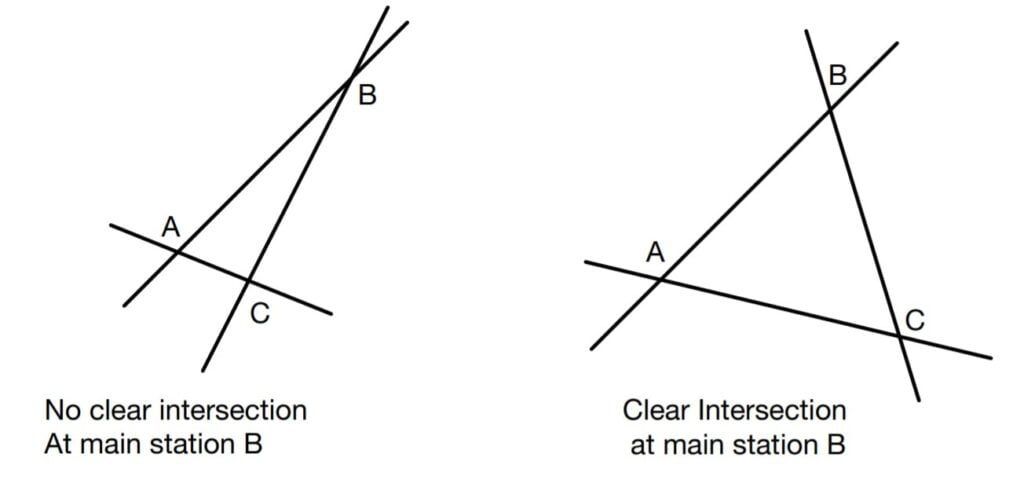
Linear Measurements with Chain
It can be done by any of the following methods.
1. On Smooth Level Ground
For measuring a distance longer than one chain length, It is necessary to establish an intermediate point via ranging. For this purpose two persons are required (leader and follower). Leader moves forward along the survey line and goes on inserting arrows at the end of the chain and the follower helps collect it. Thus at the end of measurement the number of arrows collected by the follower indicates the number of chain length measured.
2. On Sloping Ground
In a plane serving, the distance measured should be horizontal. But in certain cases, the change in elevation from one end of the chain to the other end is so large that the change cannot be kept horizontal.
In such cases chaining is done using any of two methods.
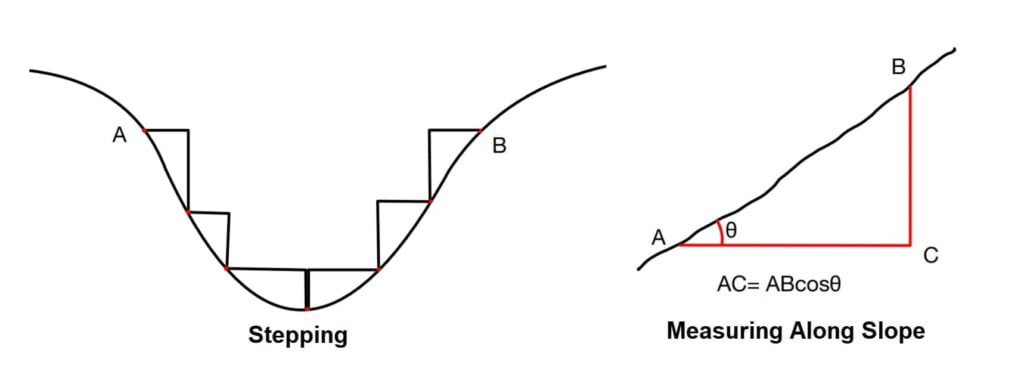
A). Stepping: Used when slope is variable.
B). Measuring Along Slope: Used when slope is constant.
Errors & Correction in Chaining/ Taping
Error is defined as difference of measured length & true length.
Error = Measured value (Measured taken at site) – True value.
Correction = True value – Measured value.
Error = -Correction
Type of Error in Chaining
- Mistakes
- Cumulative/ Systematic error: This error is directly proportional to length of the line and maybe positive and negative.
- Compensating/ Random error: this error is directly proportional to the square root of the length of line to be measured.
Correction in Chaining & Taping Are Following Type
Correction For Standardisation
This is valid for both chain & tape. This correction is applied due to the incorrect length of chain/tape.
Let
l’ = the nominal length/ wrong length of chain/tape.
l = The true length of chain/tape.
L’ = wrong length of line measured.
L = correct length of line measured.
Correct Length(L) = Actual Length of chain (l) × (no of times the chain was used to measure the length) of line.
L= l×\(\frac{L’}{l’}\)
L= \(\frac{l}{l’}\)×L’
Note: The same concept can be used for area and Volume.
True area = (l÷l’)2× measure area.
True volume = (l÷l’)3× measure volume.
Correction for standardisation (Cs)= True length- Measured Length.
Cs = L- L’
Cs= \(\frac{l}{l’}\)× L’- L’
Cs= L’×(\(\frac{l}{l’}-1\))
Cs= L’×\(\frac{l-l’}{l’}\)
Correction for Slope (Cg)
It is valid for both chain and tape.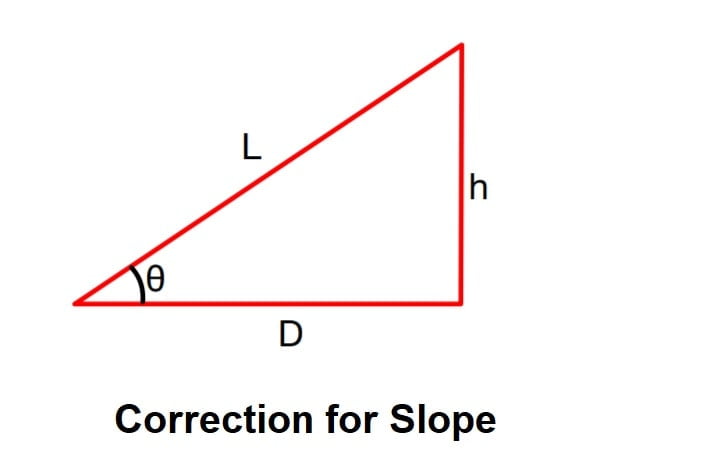
Cg = D-L.
A). When slope angle θ is known
Cg = Lcosθ – L
Cg = -L (1-cosθ)
Νote: slope correction is always negative.
B). When difference of elevation (h) is known
Cg= D-L
\(Cg=\sqrt{L^{2}-h^{2}}-L\) Exact Relation
\(Cg= \frac{-h^{2}}{2L}\)
Note: If higher power is not neglected the correction increases by \(\frac{h^{4}}{8L^{3}}\).
Correction for Pull (Tension)
If the pull applied to the tape during measurement is more than the standard pull at which tape was the standardized, then length of tape increases hence the distance measured becomes less than actual distance. Thereby the correction applied is positive. This correction is negative if the applied pull is less than a standard pull.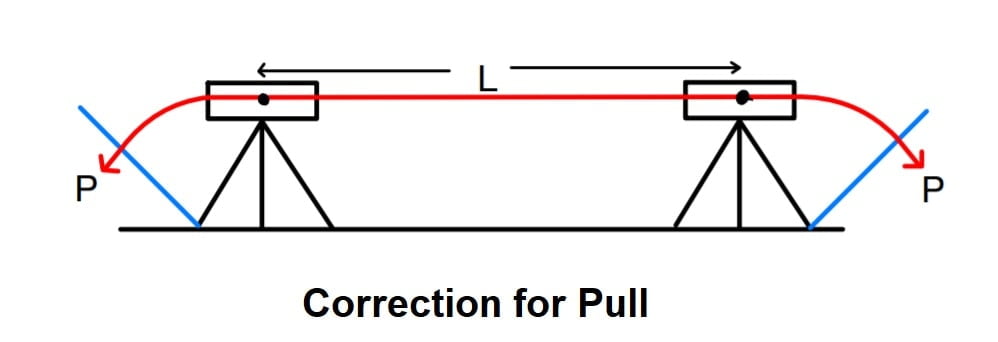
\(E=\frac{σ}{ε}=\frac{Δσ}{ε}\).
\(E=\frac{P-Ps}{A\frac{Cp}{L}}\).
\(Cp=\frac{(P-Ps)L}{AE}\)
Ps= standard pull
P= pull at the time of measurement
A= cross-section area of tape
E= modulus of elasticity of tape
L= measured length
Correction for Temperature (Ct)
The length of tape changes due to change in temperature while taking the measurement. Correction for temperature is (+ve), if the temperature during measurement is more than the standard temperature & negative(-ve) if the temperature during measurement is less than the standard temperature.
Ct= α•(Tm – T0)L
If
where
α= coefficient of thermal expansion.
Ct= correction for temperature
Tm= mean temperature during measurement
T0= temperature of standardisation
L= measured length
Correction for Sag (Csag)
If higher accuracy is required, rather than laying the tape along the ground, it can be suspended between tripod heads i.e hung in catenary and a correction for a sag in the tape is applied if the tape has been standardized on the flat.
For determination of correction, the sagged curve is assumed to be parabola
Sag correction Csag= \(\frac{-w^{2}l^{3}}{24p^{2}}\)
Where
w= weight of tape per unit length in N/m.
l= length of tape suspended between support in m.
p= applied pull in Newton.
the sag correction is always (-)ve.
Reduction of length to mean sea level (MSL)
The measured length at different altitudes are sometimes reduced to a common level, generally MSL. we know that the earth is spherioidai in shape, the measured distance at any altitude h above the mean sea level would be greater than the equivalent length at mean sea level.
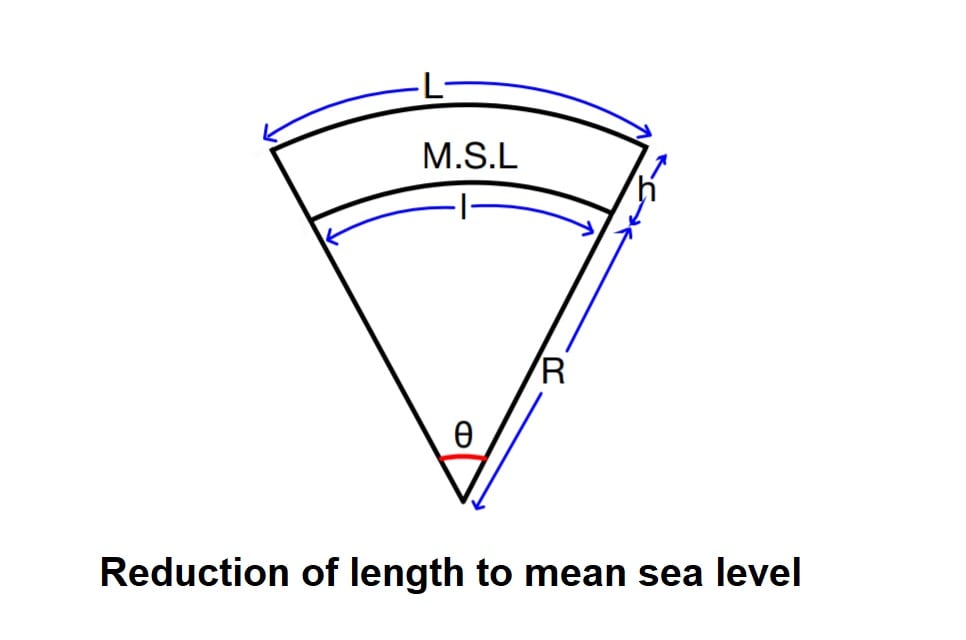
L= θR+ θh
\(θ=\frac{l}{R}\)l= θR
Cmsl= true value- measured value
Cmsl= l- L= θR- (θR+ θh)
Cmsl= -θh
Cmsl= –\(\frac{L}{R+h}\)×h (h<<R, so R+h≅ R)
Cmsl= –\(\frac{L}{R}\)×h
This correction is always negative.
Field Work in Chain Surveying
The field work in chain surveying can be divided into the four stages:
- Reconnaissance
- Marking of Stations
- Running Survey lines
- Taking Offsets
1).Reconnaissance
Reconnaissance is the preliminary inspection of the area to be surveyed to get some idea of the terrain and identify the principal features of the ground.
In a reconnaissance survey, the surveyor thoroughly examines the ground and decides upon the best possible arrangement of triangles. Best suitable positions of the main survey stations and survey lines are then selected.
2).Marking of Stations
After completing reconnaissance, the main stations are being marked on the ground such that the stations can be readily located afterwards, if required.
3).Running Survey Lines
Survey lines are run to measure the distance between main stations and to locate the adjacent details by offsets. Chaining usually commenced from the base line and continued to other survey lines.
4).Taking Offsets
As already defined, offsets are lateral distances measured from the survey line to the station whose detail is to be plotted. The offsets are of two types
- Perpendicular offsets or simply offsets
- Oblique offsets or ties
Limiting Length of Offsets
The maximum length of an offset is generally determined for the consideration that the error produced in plotting the detail on the drawing sheet should not be significant. In other words, the displacement of the detail on the drawing sheet from its correct position should not be greater than 0.25 mm or so. A good draughtsman can distinguish a distance on the paper equal to 0.25 mm.
Maximum length of the offset depends upon the
- Scale of plotting
- Possible error in direction and length
- Accuracy desired
Error in laying offset may be due to following
- Error only in laying offset
- Error in laying and linear measurement
1).Error only in laying offset

P= actual point on ground
P1= point located on paper
θ = error in laying direction.
Length of error on ground= PP2= lsinθ
If scale of map is 1cm = s meters
Length of error on paper= \(\frac{lsinθ}{s}\) cm.
For limiting length of offset:
Length of error on paper< 0.025cm
\(\frac{lsinθ}{s}\)< 0.025
l< \(\frac{0.025s}{sinθ}\)
2).Error in laying direction and liner measurement
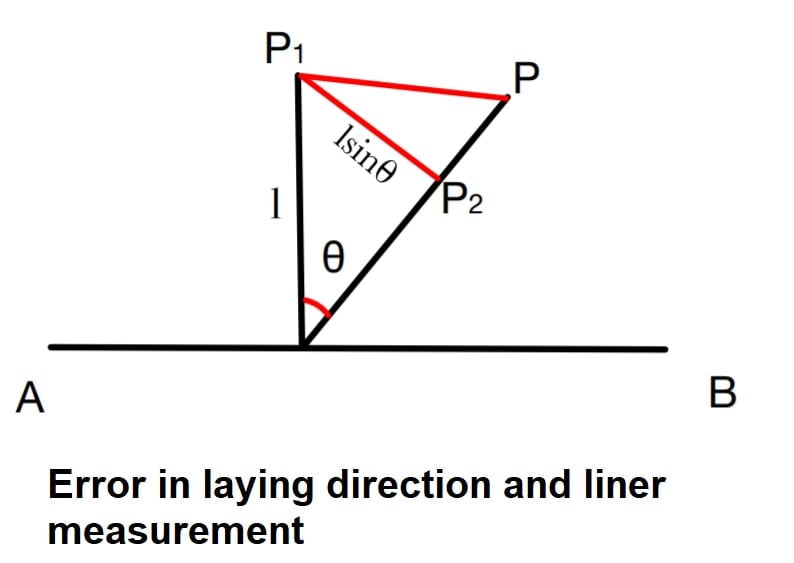
P= actual point on ground
P1= point located on paper
θ = error in laying direction.
x= error in linear measurement
length of error on ground PP1=\(\sqrt{(lsin\theta )^{2}+x^{2}}\)
If scale of map is 1cm = s meters.
Length of error on paper=\(\frac{\sqrt{(lsinθ)^{2}+x^{2}}}{s}\)
For limiting length of offset:
Length of error on paper< 0.025cm
\(\frac{\sqrt{(lsinθ)^{2}+x^{2}}}{s}\)< 0.025
l< \(\frac{1}{sin\theta}\sqrt{(0.025s)^{2}-x^{2}}\)
Note
If offset length is measured with an accuracy of 1 in r. Then error in linear measurement x= l/r.
Direct and indirect ranging?????
It is good
I like these notes.