Geometric Design of Highway
Geometric Design of a highway deals with all the dimensions and layout of visual features of a highway such that it provides maximum efficiency and minimum cost and reasonable safety.
Geometric Design of a highway depends on several design factors:
- Cross-section Element
- Sight Distance
- Horizontal Alignment Details
- Vertical Alignment Details
- Intersection Details
For designing Highway elements, the following factors are considered:
- Topography
- Design Speed
- Traffic Factors
- Design Hourly Volume and Capacity
- Environmental And Other Factors
A. Topography or Terrain:
The topography or terrain conditions influence the design speed, than in turn governs the designing of highway elements.
The classification of topography is based on the cross slope of the country as Plain, Rolling, Mountainous and Steep.


For Example in plain terrain On the state highway permissible design speed is 100 km/h, whereas the same speed on rolling terrain is permitted to 80 km/h & on mountain terrain is 50 km/h.
B. Design Speed:
The design Speed of the vehicle depends upon the type of Topography or Terrain Classification and the road over which it moves. Example- National Highway, State highway, Major district Road, Other district Road, Village Road and.
The design speed of the vehicle helps in deciding the: cross-section element, width, clearance, side distance, the radius of the curve, superelevation, transition, gradient, length of the submit curve, etc.
C. Traffic Factor:
Traffic factors include vehicle characteristics and human characteristics.
To design highway elements standard size of the vehicle is considered (car) in case of mixed traffic operation.
Human characteristics include the physical, mental, and psychological characteristics of drivers and Pedestrians.
D. Design Hourly Volume & Capacity:
The traffic volume fluctuates over time, hence the designing must be done for peak hours, but it will be highly uneconomical to do so.
Hence designing is being done for a reasonable value of traffic volume termed as “Design Hourly Volume”.
E. Environmental Factor:
Environmental factors such as aesthetics air pollution, noise pollution, and landscaping also govern the design of Highway elements.
Cross Section Elements:
Cross-section elements of pavement are critical features that impact the pavement’s longevity, riding comfort, and safety. Here are the key cross-section elements of the pavement:
- Pavement Surface Characteristic
- Cross- Slope / Camber
- Width of Pavement or Carriageway
- Divider /medians / Traffic Separators
- Kerb
- Shoulder
- Road Margin
- Roadway / Width of Formation
- Road Land / Right of Way
Pavement Surface Characteristic
Pavement surface characteristic depends upon pavement type. Which in turn depends on the availability of material, cost, composition of traffic, climate conditions, and method of construction available. Pavement surface characteristics include:
- Skid and Slip
- Friction
- Unevenness Index
- Light Reflecting Characteristic
- Drainage
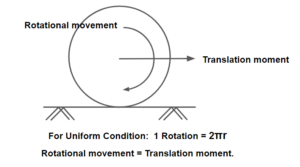
(i) Skid and Slip:
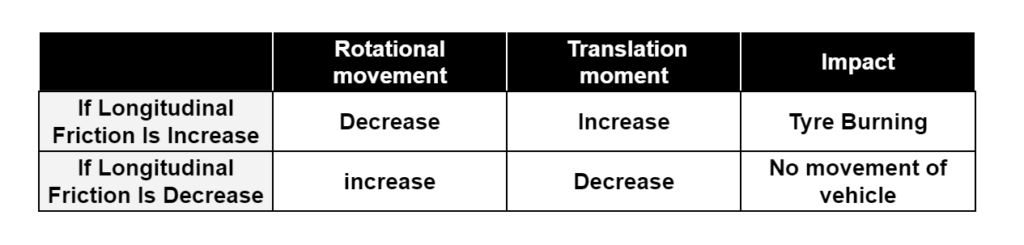
Skidding takes place when there longitudinal moment of the wheel is more than rotational movement during the break(T.M>R.M). To avoid skidding, friction resistance must be greater than the braking force.
For Pure Skid, Rotational movement =0, Translation moment ≠0.
Slipping occurs when the wheel revolves more than the corresponding longitudinal movement along the roads during acceleration(R.M>T.M). It generally occurs on a pavement surface that is either slippery and wet or when the road surface is with mud.
For Pure slip, Rotational movement ≠0, Translation moment=0.
(ii) Friction:
- It decides the operating speed and Minimum distance required for stopping the vehicle.
- Maximum friction is developed when breaks are applied up to a complete extent.
- Friction also governs the rotational transitional moment of the wheel.
- It is further classified into two:
- Longitudinal Friction
- Lateral or Transverse Friction
(A) Longitudinal Friction:
Longitudinal friction helps support the movement of the vehicle.
Longitudinal friction depends upon speed, For high speed friction is less.
(B) Lateral or Transverse Friction:
Lateral friction comes into the picture only when there is a lateral force on the vehicle.
NOTE– As per IRC, the coefficient of longitudinal friction lies between 0.35 to 0.40, used in sight distance calculation, and the coefficient of lateral fiction is 0.15, used in horizontal curve design.
Friction depends on the following factors:
Type of pavement surface (CC, Bitumen, Earthen material, WBM).
Roughness of the pavement (Texture).
Condition of pavement (Dry, Wet, Rough of smooth).
Condition of tyres ( New with good threads or old with worm-out threads).
Speed of vehicle.
Extent of break application ( Full or Partial).
Load and tire pressure.
The temperature of tire and pavement: On the Dry Surface coefficient of friction of old tyre is greater than the new tyre. On the wet surface coefficient of friction of the old tire is lesser than the new tire.

Note: Hence new tyre is more dependable in adverse conditions. Examples – Wet surface.
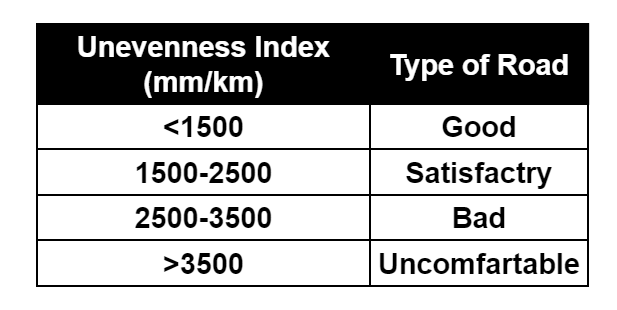
(iii) Unevenness Index:
The presence of undulations on the Pavement surface is called Unevenness.
The Unevenness index is defined as cumulative undulation per kilometre of road length.
It is expressed in terms of mm/Km.
It is measured by BUMP INTEGRATOR. (Developed by CRRI)
Uneven surface increases riding discomfort, fuel consumption, wear and tear of tyres and other part,s and accidents.
The different values of the Unevenness Index and the corresponding serviceability of road is as follows:
Note- Internationally Roughness is measured in term of IRC ( IRC=INTERNATIONAL ROUGHNESS INDEX).
\(BI=630(IRI)^{1.12}\)
BI = BUMP INTEGRATOR (mm/km)
IRC=INTERNATIONAL ROUGHNESS INDEX (m/km)
Unevenness of the pavement depends upon the following factors.
Improper Compaction.
Use of improper construction method.
Use of interior quality material.
Improper surface and sub surface drainage.
Poor maintenance of pavement surface.
(iv) Light Reflecting Characteristic:
Visibility over the pavement surfaces depends upon its color and light characteristics.
The glare caused by the reflection of the headlight is higher on wet pavement surfaces than on dry pavement.
Light-colored pavement surfaces give good visibility at night but produce more glare during the daylight while on the other hand black too pavement has poor visibility at night.

(v) Drainage:
The pavement must be completely impermeable so that seepage of water into the pavement layers does not take place and the geometrical pavement surface should be such that it helps and remains out of the water from the surface quickly.
Camber / Cross- Slope:
- It is the slope provided to the road surface in the transverse direction to drain the rainwater from the road surface to avoid the following:
- Stripping of bitumen from the aggregate in the presence of the water.
- To avoid swelling of subgrade in case water seeps up to it.
- The slipping of the vehicle over the wet pavement.
- Glare over the wet pavement surface.
- On a straight Road, it is provided by raising the center of the carriageway concerning edges forming the crown on the highest point along the center line.
- At a horizontal curve with superelevation, the surface drainage is provided by raising the outer edge.
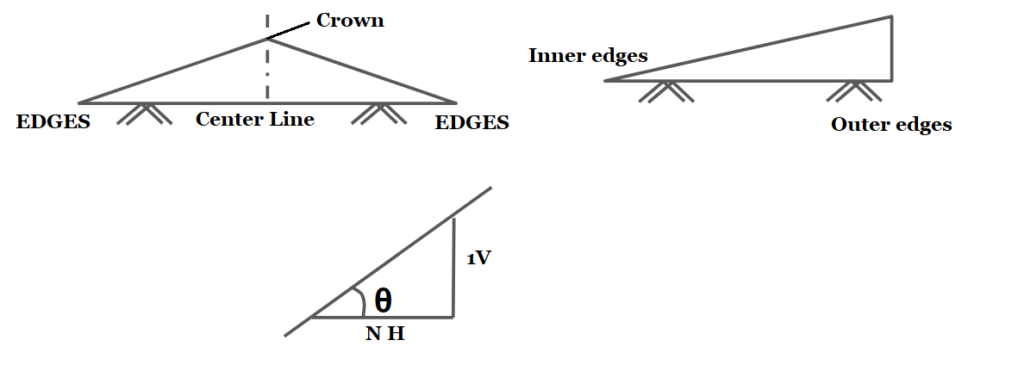
- It is represented in any of the following ways:
- As percentage :For example cross-section 5% ⇒ tanθ = \(\frac{5}{100}\).
- As fraction : For example cross- section = 1 in 20 = \(\frac{1}{20}\) = 0.05.
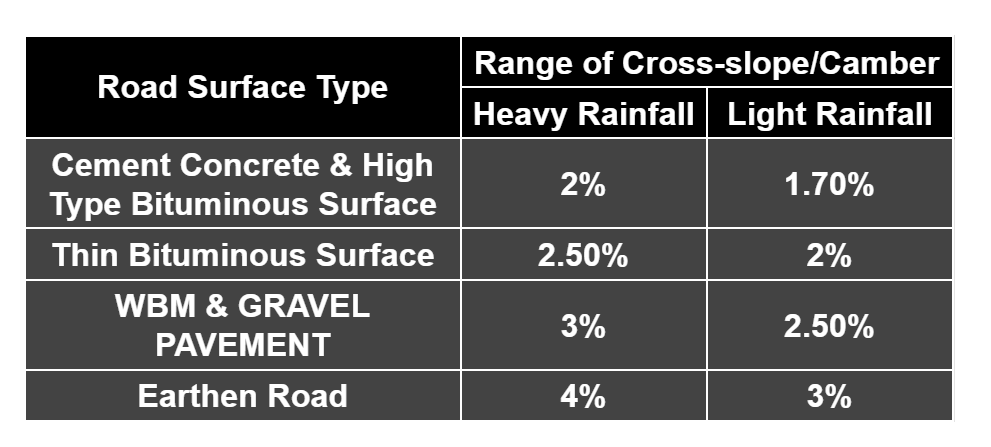
- The value of the cross-section depends on the following factor:
- Type a pavement surface
- Amount of rainfall
Type of Cross-Slope / Camber
- Straight line Camber
- Parabolic Camber
- Composite Camber
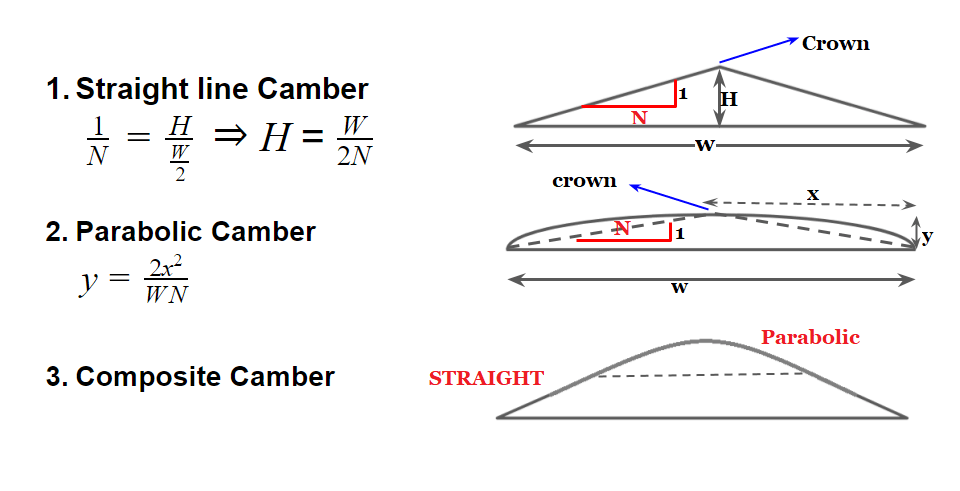
Note: For cement concrete pavement straight line camber is preferred. As it is easier to lay.
Gradient = 2x Camber
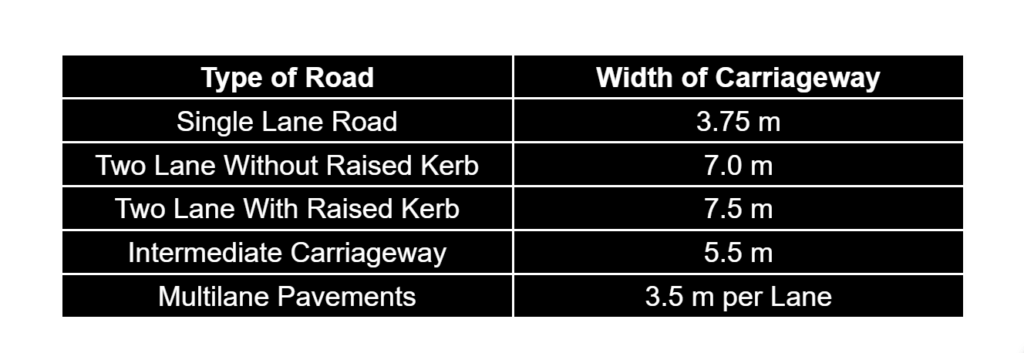
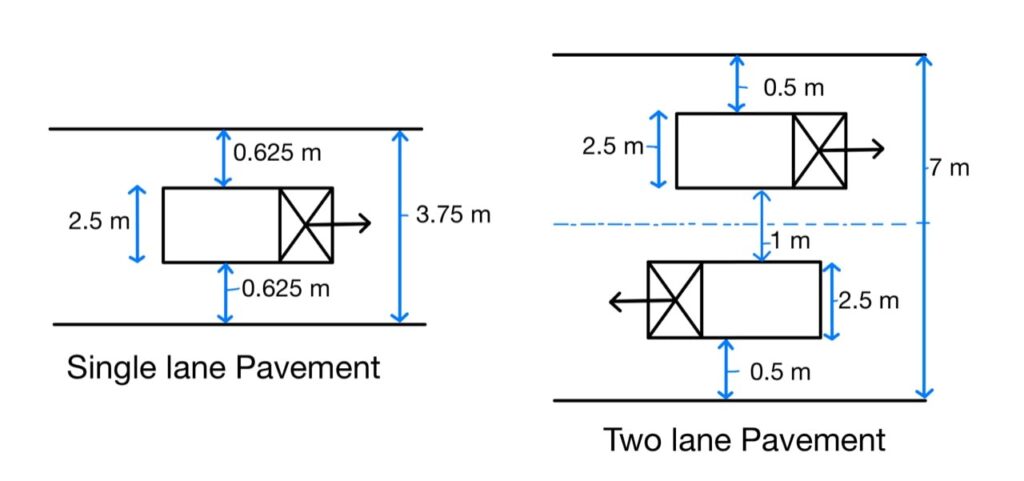
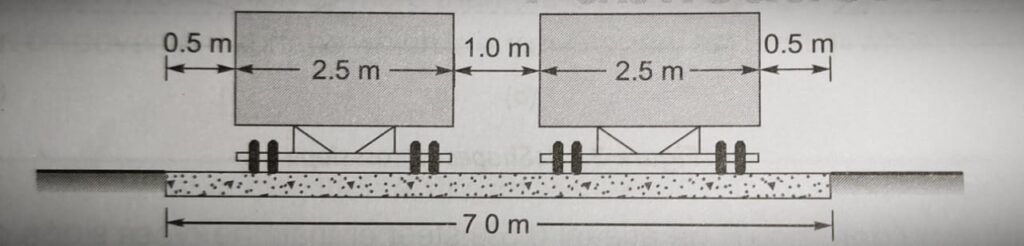
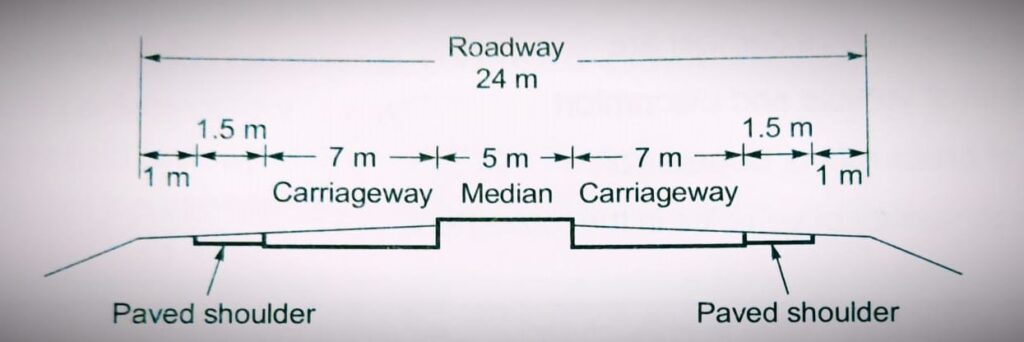
Width of Pavement or Carriageway
- The width of payment depends upon the width of the traffic lane and number of lanes.
- Width of traffic lane is decided on the basic the type of vehicle moving on it, along with same clearance in both the sides.
- Passenger car is considered as a standard vehicle to decide the width of carriageways. (Width of passenger car = 2.44 meter= 2.5 meter)
- For rural highway, if pavement has two or more lane, width of single lane is 3.5 meter.
- The number of lane to be provided depends upon traffic volume.
- The width of carriageway for different conditions are follow.
Divider /Medians / Traffic separators
- Divider is an element provided to the Road along the center line to separate two-way traffic. The main function of the median is to prevent “Head-on collision” between vehicles moving in the opposite direction. it also serves the following other functions:
- To channel traffic into the streams.
- To protect the pedestrians.
- The glaring effect due to the Headlight of the opposite direction vehicle can be reduced.
- To segregate the slow traffic.
- Medians can be provided in the following forms:
- As pavement marking
- Physical dividers (Mechanical separator)

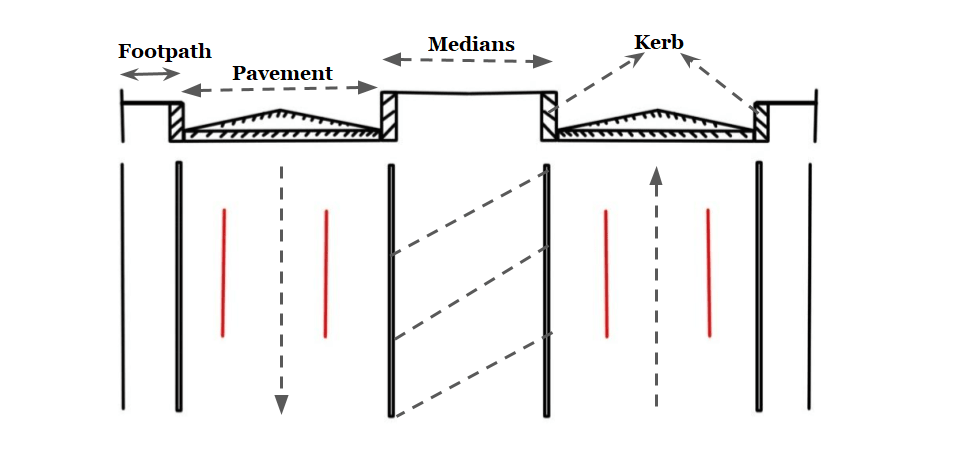
- The desirable width of the median is 8- 14 meters. ( It includes the provision for future expansion of roads)
- To reduce the glare of the light of the opposite moving vehicle minimum width required is 6 meters.
- IRC recommended a minimum width of 5 meters for the divider which can be reduced to 3 meters where land is restricted.
- On the bridge width required for the median is in the range of 1.2 to 1.5 meters.
- In urban areas, the minimum width of the median to be provided is 1.2 meters & desirable min is 1.5 meters.
- For the Expressway the minimum width to be provided is 12 meters and the desirable is 15.5 meter.
Kerb
Kerb is a separator between pavement & footpath. It provided lateral support to the pavement. Kerb is mainly divided into the following 3-categories.
- Low or Mountable type Kerb
- Semi- Barrier-type Kerb
- Barrier type Kerb
1. Low or Mountable type Kerb:
The height of this type of kerb is about 10 cm with a slope or batter to help the vehicle climb the kerb easily.
2. Semi- Barrier type Kerb:
The height of this type of Kerb is about 15 cm with a batter of 1:1 on the top 7.5 cm. It is provided where pedestrian traffic is high. (Pedestrian = A person who is walking in the street.)
3. Barrier type kerb:
The height of kerb stone is about 20 cm with a batter of 1:4.
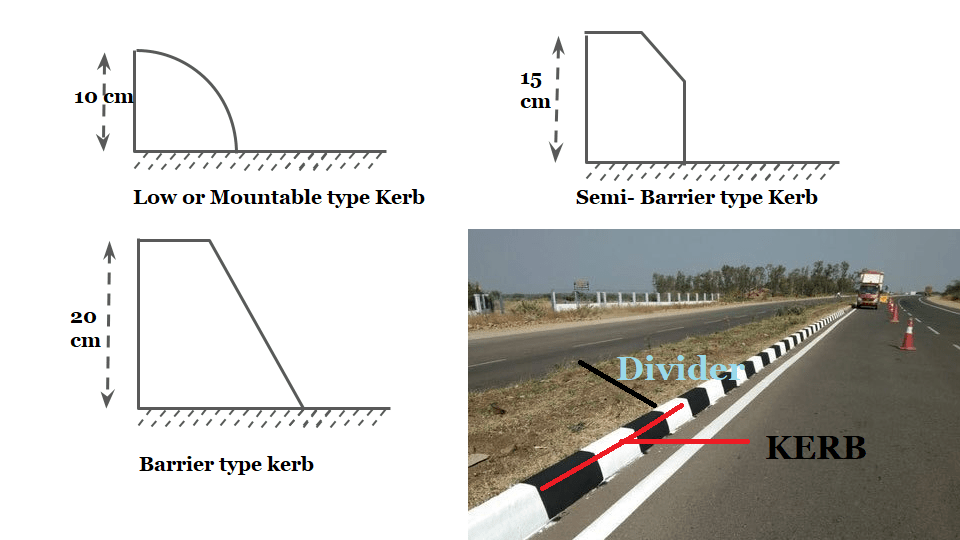
The functions of kerb are:
- To facilitate and control drainage.
- To delineate the pavement edge.
- To present a more finished appearance.
- To strengthen and produce the pavement edge.
Shoulder
- The extra width provided adjacent to the edge of the pavement is called the shoulder. It is provided for emergency points of view like Breakdown of vehicles, medical emergencies, etc.
As per IRC
- The minimum width of the shoulder required for a highway is 2.5 meters.
- The cross slope of the shoulder should be 0.5% more than the cross slope of the adjoining pavement, having a minimum value of 3% & maximum value of 5%.
- 5% ⊀ cross slope(shoulder)= (0.5%+ cs of pavement) ⊀3%.

Slope of Shoulder
Road Margin:
These are the areas which are not used as regular roadways. The various elements included in the road margins are as follows:
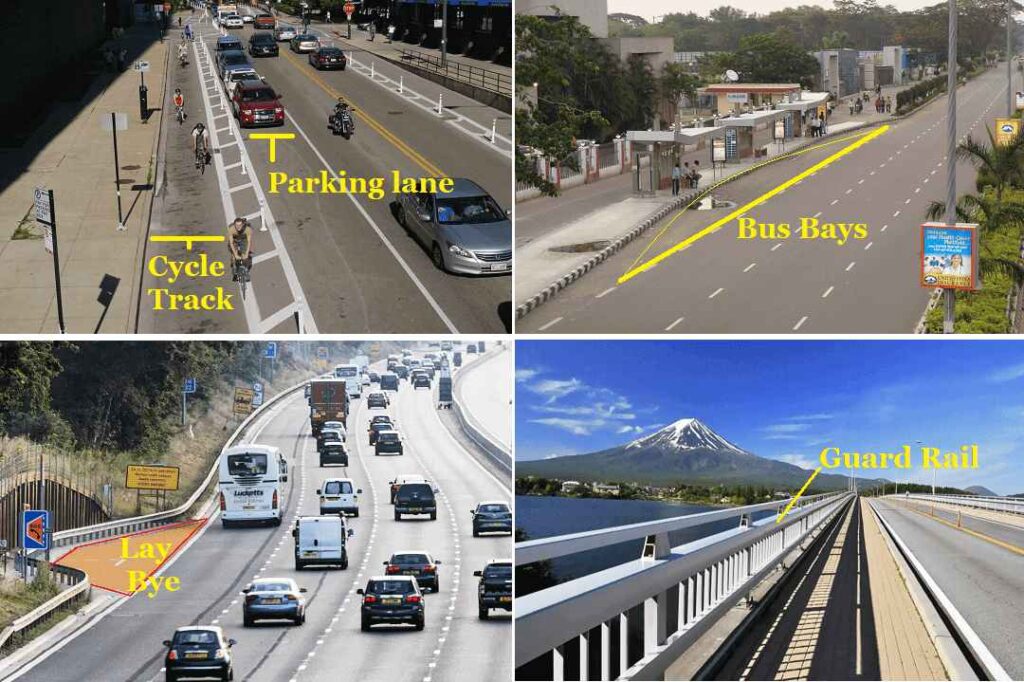
- Parking lanes: These are generally provided on an urban road to allow car parking. Parallel parking is generally provided for the safe moving of vehicles. However, angle parking is also provided. The parking lane should have sufficient width. For parallel parking 3.0 m width is required.
- Lay Bye: These are provided near public convenience to avoid conflict with a running traffic minimum width is 3 meters.
- Cycle Track: These are provided in urban areas for the safe movement of cycle traffic. The minimum width required is 2 meters for the cycle track and it can be increased by 1 m for each additional cycle lane.
- Driveways: these are used to connect the highway with commercial establishments like fuel stations, service-station, etc.
- Footpath: These provide urban roads having heavy vehicular as well as pedestrian traffic, to protect pedestrians. The minimum width of the footpath should be 1.5 m and it may increase based on the pedestrian traffic volume.
- Guard Rail: These are provided at the edge of the shoulder when the road conditions fill to prevent vehicles from running off the embankment. Guard stones are installed at a suitable distance to provide better night visibility on the curves under the headlights of the vehicle.
- Service Road: These are provided parallel to the highway and isolated by a separator and access to highways is provided only at selected points. They are provided to avoid congestion on the highway and expressway.
- Bus Bays: It may be provided by recessing the kerb to avoid conflict with the moving traffic and must be located at least 75m away from the intersection. It is used for safe plying of Passenger and Cargo from Bus.

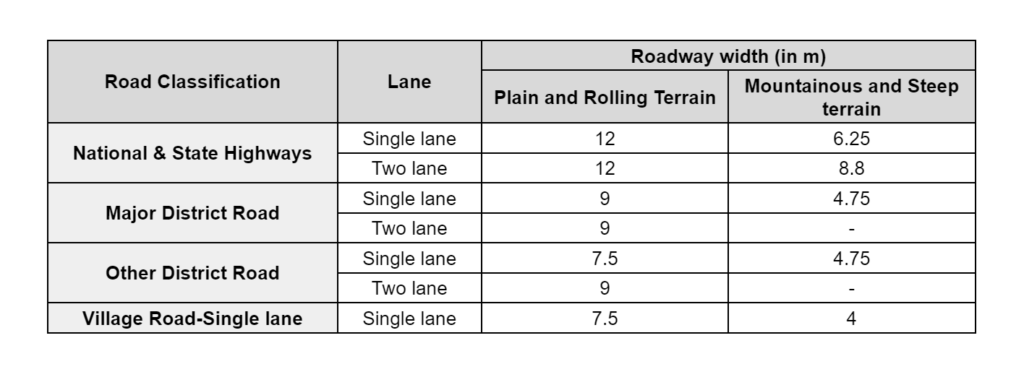
Roadway / Width of Formation:
- It is the sum of with pavement or carriageway including the separator (if any) and the shoulder.
- Roadway width is the top of the highway embankment or bottom width of highway cutting excluding the side drain.
- Width of the Formation of various classes of Road is as follows:
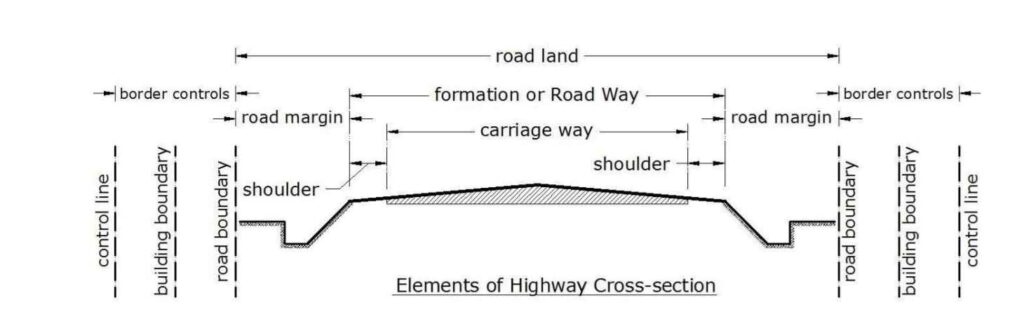
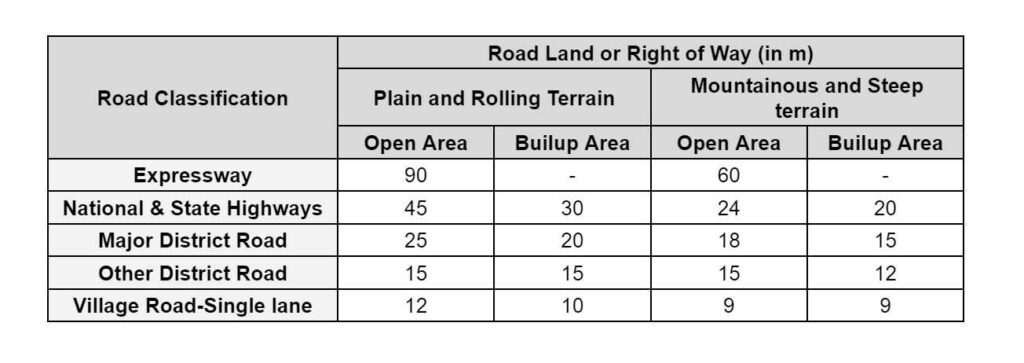
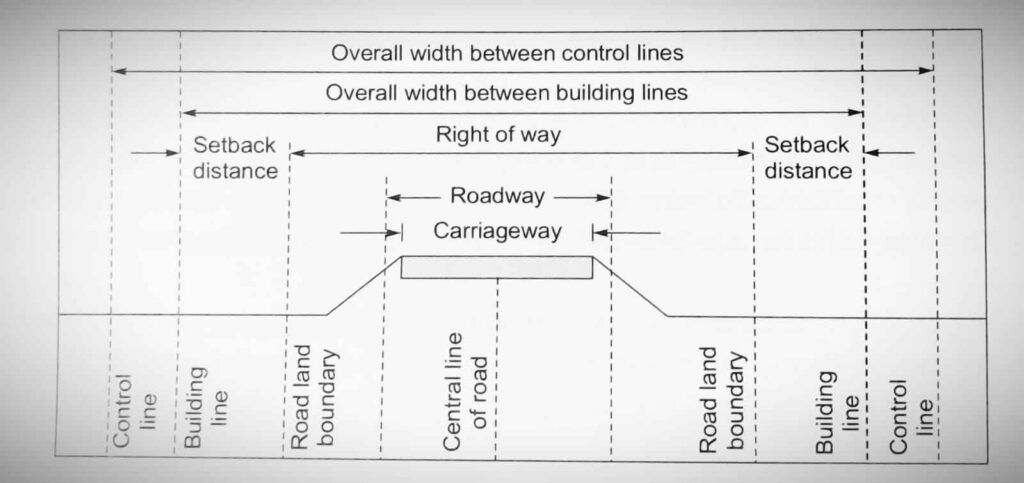
Right of Way / Road Land:
- It is the area of the land acquired for the road along its alignment keeping In view its future expansion also.
- Construction of a particular type of building is only permitted with sufficient setback from the road boundary up to the Central line.
- Width of land for different roads in rural areas or as follows:
Sight Distance
Sight distance is the length of the road visual ahead to the driver at any distance. ( it is considered by taking the height of the eyes of the driver to be 1.2 m and the height of the object to be 0.15 m).
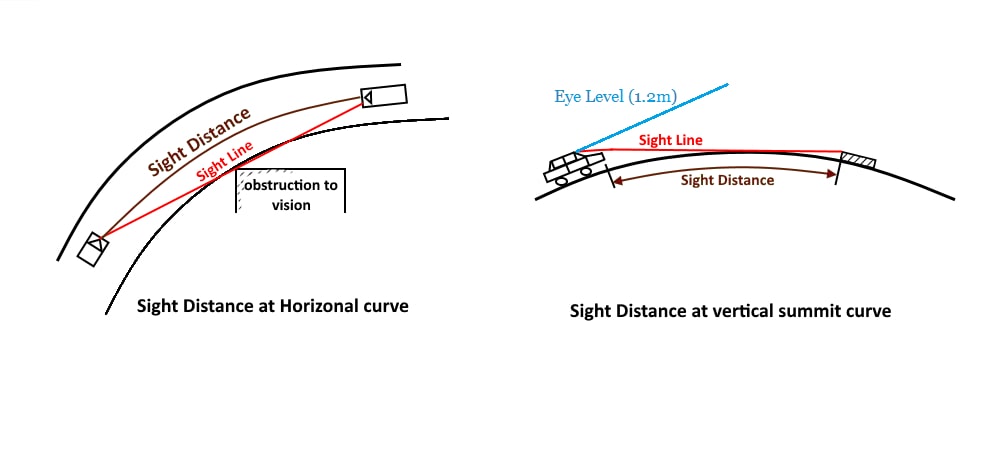
Restriction to the visibility/sight distance may be caused in the following cases:
- At a horizontal curve, when the line of sight is obstructed by the object and the inner side of the curve.
- At a vertical curve the line of sight age of obstructed by the road surface of the curve.
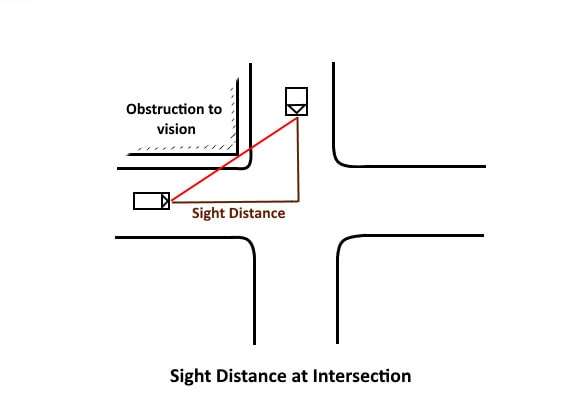
- At an uncontrolled intersection when a driver from one of the approach road is able to sight a vehicle from another approach road towards it at the intersection, due to the presence of obstruction.
The sight distance available to the driver depends upon the following factors:
- Feature of road ahead: Horizontal curve, vertical profile, traffic condition, position of obstruction.
- Height of driver’s eyes above the road surface.
- Height of object above the road surface.
Sight distance on a highway depends upon the following factors:
- Total Reaction Time of Driver
- Design speed
- Braking Efficiency
- Frictional Resistance Between Road and Tyres
- Gradient of Road
1. Total Reaction Time of Driver
- It is the time taken from the instant the object is visible to the driver to the instant brakes and applied effectively.
- The total reaction time is further divided into different components and can be explained as follows:
- Perception(P): The time required for the sensation received by the eyes or ears of a driver to be transmitted to the brain through the nervous system and spinal cord.
- Intellection Time (I): it is the time required to the driver to understand the situation. It is also the time required for comparing different thoughts, regrouping & registering new sensations.
- Emotion Time (E): It is the time elapsed during emotional sensations and other mental disturbances such as fear, anger, superstition, etc with the situation to come into play. This time varies from person to person and even for the same person in different situations.
- Volition Time (V): It is the time taken by a driver, for final action, like application of brakes.
- The above can be termed as “PIEV” analysis for Total Reactions Time.
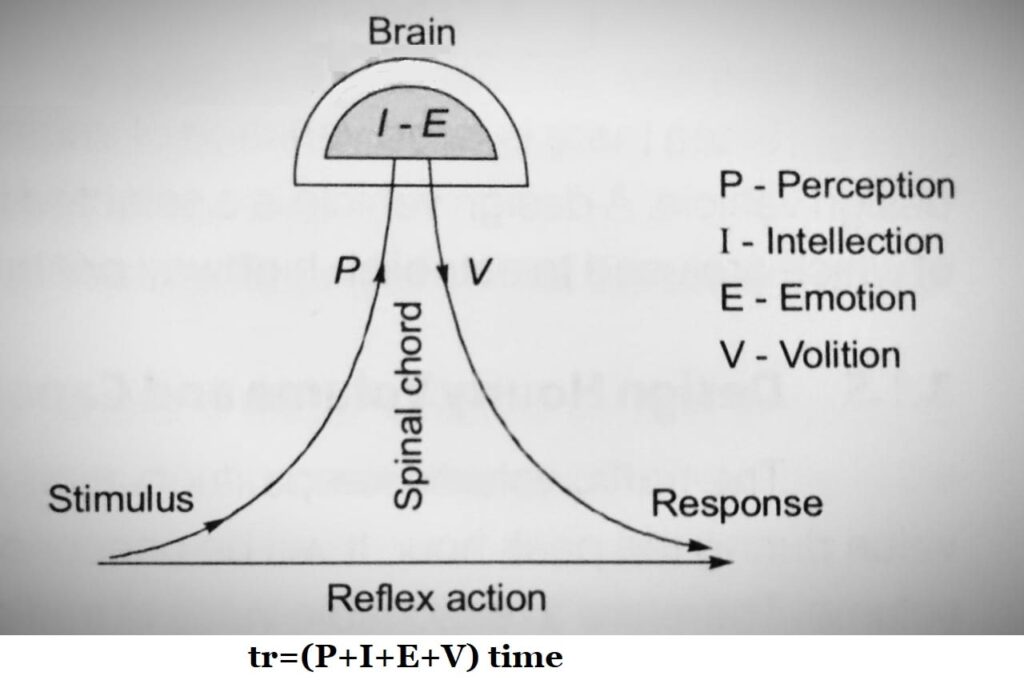
Note:
- It is also possible that the driver may apply brakes or take any other avoiding action, like turning, by the reflex action, without a normal thinking process, that is observed to be in time for avoiding the collision.
- This reaction time depends on several factors like driver skill, type of obstruction involved, environmental condition, age, etc
- Total reaction time is measured based on PIEV theory which varies from 0.5 seconds for simple situations to 3-4 seconds for complex situations.
Remember:
IRC recommended a reaction time of 2.5 seconds for stopping sight distance and 2.0 seconds for overtaking sight distance calculations. And 0.7 seconds for Minimum Spaceheadway.
| tr in seconds | |
| SSD | 2.5 sec |
| OSD | 2 sec |
| Minimum Space Headway | o.7 sec |
2. Design Speed
- During the total reaction time of the driver, the distance moved by the vehicle depends upon design speed.
- If the speed of the vehicle is not mentioned in the problem then consider the design speed of the highway as the speed of the vehicle.
- Braking distance means the distance traveled by the vehicle before coming to a stop/half and also depends on design speed.
3. Braking Efficiency
- The efficiency of brakes depends upon the age and characteristics of the vehicle. If we say the brakes are 100% efficient, it means the vehicle will stop at the moment of application of brakes. But practically 100% efficiency update is not achieved, otherwise skidding will occur which is uncontrollable and dangerous for the vehicle and road users.
- For the design purpose of the highway, we considered 50% brake efficiency of the vehicle.
4. Frictional Resistance Between Road and Tyres
- The frictional resistance developed between the road and tyres depend on the coefficient of friction.
- The higher is coefficient of friction, the higher is the frictional resistance and the lower is SSD.
- The coefficient of friction further depends upon the condition of tyres and roads.
- It is further linked with the design speed of a vehicle as follows:

5. Gradient of Road (If Any)
- When we are going down on a gradient, the gravitational force also comes into action which causes the vehicle to take more time to stop vehicle means more sight distance is required. While climbing up a gradient less sight distance is required because the time taken to stop the vehicle will be less.
Sight distances are of the following types:
- Stopping Sight Distance (SSD).
- Safe Overtaking Distance (OSD).
- Intermediate Sight Distance (ISD)
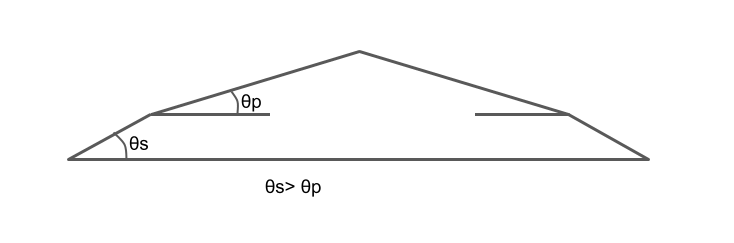
Sight distance at Intersections
Note: where we use v it means speed in meter/second and where we use V it means speed in Km/hr.
1. Stopping Sight Distance (SSD):
The minimum distance visible to a driver ahead to safely stop a vehicle traveling at design speed without collision with any other obstruction is termed as “SSD”. It is also termed as “Absolute Minimum Sight Distance” or ” Non-Passing Sight Passing”.
Assumption
- Height of the driver’s eyes H= 1.2 m.
- Height of obstruction h= 0.15m
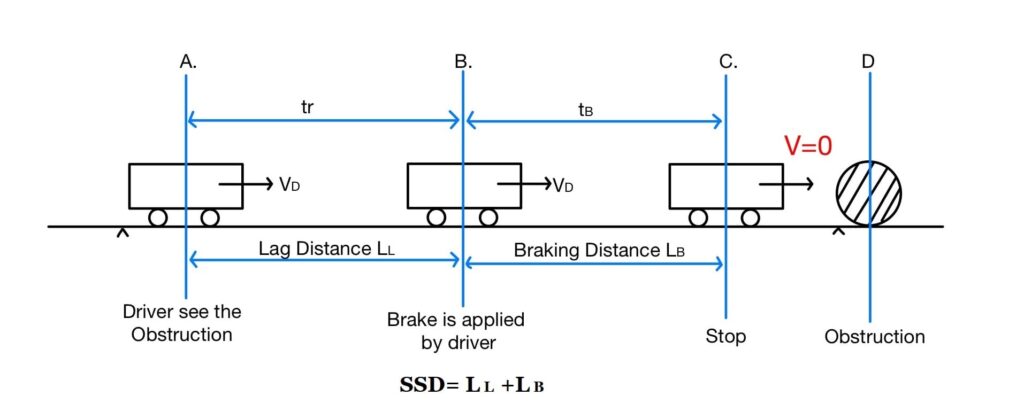
The stopping distance of the vehicle includes:
- Lag Distance (LL)
- Braking Distance([LB)
(I). Lag Distance (LL)
The distance traveled by a vehicle at uniform design speed during the total reaction time (tr) is termed “Lag Distance (LL).
LL = v×tr | v= Design Speed (m/sec). |
When Design Speed in Km/hr.
\(L_L= \frac{V\times 10^{3}}{60\times 60}\times t_r\) .
\(L_L= \frac{10^{3}}{3600}V\times tr\).
\(L_L= \frac{5}{18}V\times tr\).
| LL = 0.278×V×tr | V = Design Speed (km/hours). tr= Reaction time (sec). LL= Lag Distance (m). |
As per IRC reaction time (tr) is taken to be 2.5 seconds for SSD.
(II). Braking Distance (LB)
The distance traveled by the vehicle after the application of the brake is termed Braking Distance(\(L_B\)).
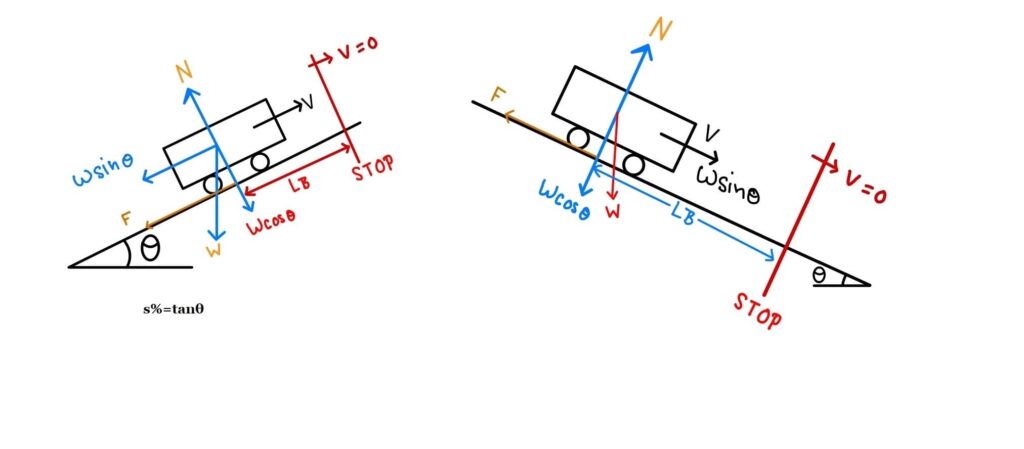
Case-1: Ascending Gradient:→
Gradient= tanθ= \(\frac{s}{100}\)= s%
| Total Resisting Force= mg·sinθ+ F | where F= Friction Force F= Normal Force×Friction Coefficient. F= f×mg·cosθ |
| Total Resisting Force= mg·sinθ + f×mg·cosθ | |
Equating the kinetic energy of the vehicle and work done to stop it.
ΔK·E= Work Done
(we know that Work Done= Force× Distance)
Unit change
\(L_B\)=\(\frac{(\frac{5}{18}V)^{2}}{2×9.81(f+s \%)}\)
\(L_B\)=\(\frac{V^{2}}{254.27(f+s \%)}\)
\(L_B\)=\(\frac{V^{2}}{254(f+s \%)}\)
Here:
\(L_B\) in meter.
V in kilometres/hours.
g in metre/second².
Case-2: Descending Gradient:
\(L_B\)=\(\frac{V^{2}}{254(f-s \%)}\)
Case-3: Flat Road:
s=0 |
SSD=\(L_L+L_B\)
SSD=\(0.278\times V\times tr\)+ \(\frac{V^{2}}{254(f±s \%)}\)
where
SSD= Stopping Sight Distance (meter)
V= Design Speed(km/hr)
tr= Reaction time(sec)
f= Friction Coefficient(unit less)
s= Gradient
or
SSD=\(v\times tr\)+ \(\frac{v^{2}}{2\times g(f±s \%)}\)
SSD= Stopping Sight Distance (meter)
v= Design Speed(m/sec)
tr= Reaction time(sec)
f= Friction Coefficient(unitless)
s= Gradient
g= m/sec2
Note:1
- SSD must be available at each & every section of the road.
- As the SSD, required on descending gradient is higher, it is necessary to determine the critical value of SSD for the descending gradient on the roads with gradient & for two-way traffic flow.
- On the restricted width or single-lane roads when two-way movement of traffic is permitted, the minimum SSD is equal to twice the SSD to enable both vehicles coming from opposite sides to stop.
For single-lane roads, two-way traffic
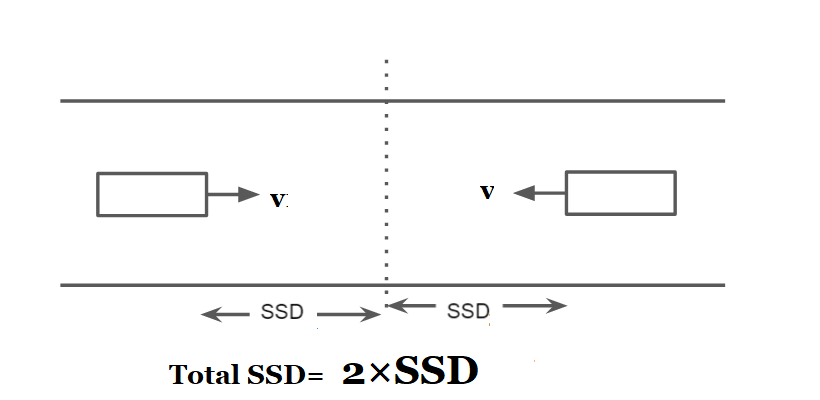
Total SSD or SD= 2×SSD when the surface is flat and the Design speed same for both vehicles.
Otherwise
Total SSD or SD = SSD1 + SSD2 when the surface is not flat and the Design speed is not the same for both vehicles.
Note:2 If Breaking Efficiency is Given
Breaking efficiency = how much amount of break you will be applying.
Assume Breaking efficiency ηB = 60 % and fmax =0.4
then f = ηB× fmax = 0.6×0.4
SD=\(0.278\times V\times tr\)+ \(\frac{V^{2}}{254(f±s \%)}\)
now f= ηB× fmax
Note:3 SD to reduce the speed from V1 to V2
SD=\(0.278\times V\times tr\)+ \(\frac{V_1^{2}-V_2^{2}}{254(f±s \%)}\)
Note:4
- If SSD can not be provided on any stretch of road due to unavoidable reasons for the design speed available, the speed should be restricted either by installing speed-limit regulation signs or by forced reduction of the speed.
- This is however temporary, and efforts must be made to provide SSD over the period of time. (By the changing alignment of the road or by removing the obstruction.)
- The SSDs recommended by IRC are as follows:

2. Overtaking Sight Distance (OSD)
- If all the vehicles fly on the road at the design speed, then theoretically there would be no need for overtaking, but practically it never happens, hence vehicle moving at the design speed has to overtake the slow-moving vehicle.
- The minimum distance open to the vision of the driver of a vehicle intending to overtake a slow-moving vehicle with safety against traffic in the opposite direction is termed OSD or “Safe Passing Sight Distance”.
- OSD is measured along the center line of the road considering the eye level of the driver at 1.2 m above the surface, observing the object at a height of 1.2 m above the surface.
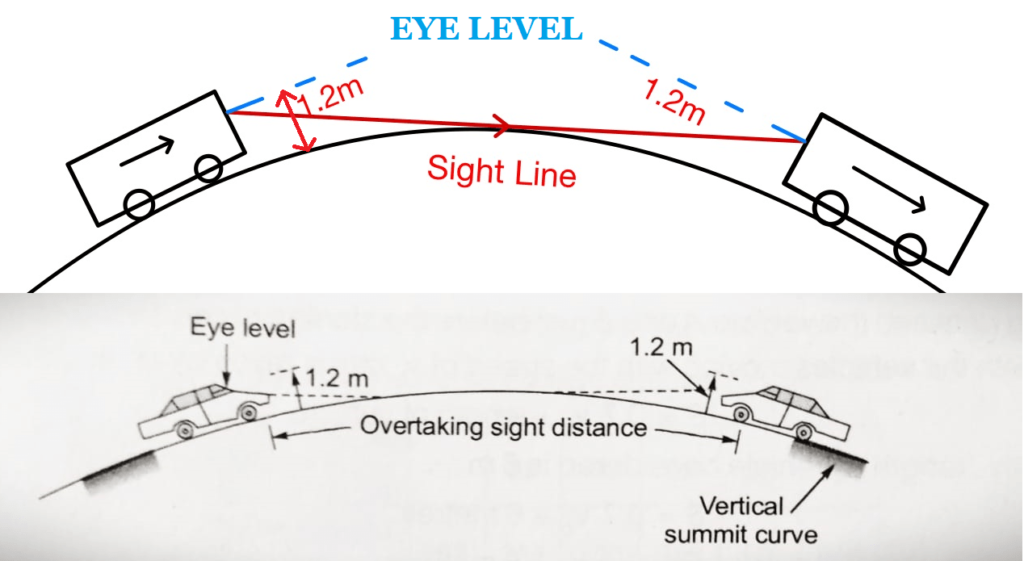
Factors affecting OSD
- Speed of vehicle, Overtaking vehicle, Overtaken vehicle, The vehicle coming from the opposite direction.
- Reaction time and skill of driver.
- Gradient of Road.
- Condition of overtaken vehicle which governs the rate acceleration.
- Distance between the two vehicles.
Analysis of OSD
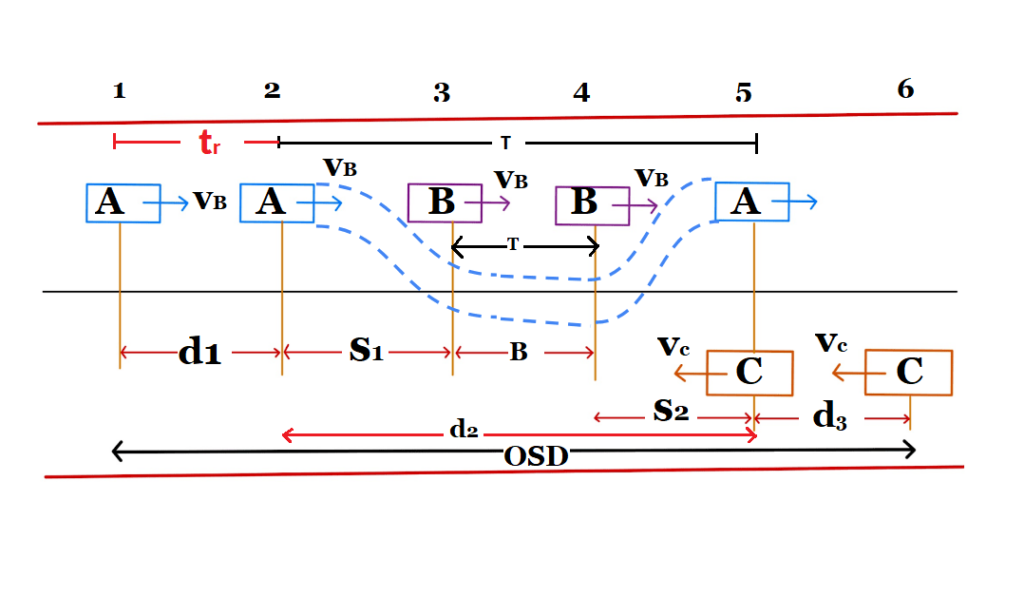
( When Vehicle A at point 2 then Vehicle B is at point 3 and Vehicle C is at point 6 after T second vehicle A moved to point 5 from 1, Vehicle B moved to point 4 from point 3 and Vehicle C moved to point 5 from point 6 )
The overtaking moment may be split up into three operations as follows:
OSD= d1 + d2 + d3 for 2-way traffic without divider
- d1:- It is the distance traveled by overtaking vehicle “A” during that reaction time “tr” of the driver, before starting to overtake vehicle B at the speed of VB.
- d2:- it is the distance traveled by vehicle “A” during the actual overtaking operation of time “T”.
- d3:- It is the distance traveled by an oncoming vehicle “C” during the actual overtaking operation of a for time “T”.
The assumption in the analysis of OSD
- Overtaking vehicles are forced to reduce speed up to the speed of overtaken vehicles for reaction time.
- When the driver of the vehicle “A” finds a sufficient clear gap, decides within a reaction time to overtake.
- Vehicle “A” accelerated and overtakes vehicle “B” within a distance d2 during the time “T”.
- The distance d2 is split in components.
- During this overtaking time “T” the vehicle “C” coming from opposite direction travel through distance d3.
case.1 For d1
As per IRC reaction time is taken to be 2.0 seconds for OSD.
VB= speed of the slow-moving vehicle (from point 1 to point 2 by vehicle A and from point 3 to point 4 by vehicle B)
To avoid confusion: From point 2 to point 5 by vehicle A, the speed of vehicle A is greater than VB, so overtaking is a possible
case.2 For d2
d2= s1+s2+B.
s1 or s2= minimum spacing between the two vehicles, which depends upon their speed. It is also termed space headway. but for design s1=s2=s (s1+s2= 2s).
d2= 2s +B.
Space Headways
| s = (0.7×vB +6) m. | vB put in meter/second. |
| s= (0.7×0.278×VB +6) m. s= (0.2×VB +6) m. | VB put in kilometers/hours. |
| B = Distance traveled by vehicle ‘B’ of speed Vb and time ‘T’. | |
| B= vB·T (where B in meter) | vB put in meter/second. |
| B= 0.278×VB×T (where B in meter) | VB put in kilometers/hours. |
d2= 2s +B
d2 = 2s + vB·T. (vB put in meter/second) ….(1)
Here also d2
d2= vB•T+ \(\frac{1}{2}\)×a·T² ….(2)
we know that [d= ut+ \(\frac{1}{2}\)at²]
a= acceleration of overtaking vehicle (m2/sec)
equation 1 = 2
2s + vB·T = vB•T+ \(\frac{1}{2}\)×a·T²
cancel vB·T both side
2s = \(\frac{1}{2}\)×a·T²
T= \(\sqrt{\frac{4s}{a}}\)
where T = overtaking time in sec
s= space headway in meter = 0.2VB+6 (VB put in kilometers/hours.)
Note
we assume s1=s2=s , (s1+s2= 2s). but if s1≠s2
then T= \(\sqrt{\frac{2(s_1+s_2)}{a}}\)
The acceleration of overtaking vehicle varies depending on several factors:
- Type of vehicle.
- Condition of vehicles (for new vehicle acceleration is high and old vehicle acceleration is low.)
- Load on vehicle.
- Speed of vehicle.
- Characteristic of driver.
Maximum overtaking acceleration at different speeds are as follows:
| SPEED (KM/H) | MAXIMUM ACCELERATION (M/SEC2) |
| 25 | 1.41 |
| 30 | 1.30 |
| 40 | 1.24 |
| 50 | 1.11 |
| 65 | 0.92 |
| 80 | 0.72 |
| 100 | 0.53 |
Note:- Overtaking time “T” of vehicle A depends upon it average acceleration “a” & speed of overtaken vehicle VB.
case.3 For d3
| d3 = Vc ·T | vc =design speed of road (m/sec). |
| d3 = 0.278·Vc ·T | Vc =design speed of road (m/sec). |
OSD= d1 + d2 + d3
| when VB and VC in km/h, tr, and T in sec |
| OSD= d1 + d2 + d3 OSD= 0.278VB·tr + 2s + 0.278VB·T + 0.278VC·tr or OSD= 0.278VB·tr + 0.278×VB•T+ \(\frac{1}{2}\)×a·T² + 0.278VC·tr |
| when vB and vC in m/sec, tr and T in sec |
| OSD= d1 + d2 + d3 OSD= vB·tr + 2s + vB·T + vC·tr or OSD= vB·tr + vB•T+ \(\frac{1}{2}\)×a·T² + vC·tr |
Note
1. For one-way traffic or two-way traffic with a divider OSD= d1 + d2. On divided Highways with one-way traffic the overtaking distance need to be only (d1 + d2) because no one expected from the opposite direction.(On divided highways, d3 need not be considered)
2. if data is not given, then the speed of vehicle A and vehicle C is the same. (VA=VB)
3. if data is not given, and Design Speed = V kmph
| VA = VC = V kmph VB = (V -16) kmph | As per IRC. |
4. For OSD & ISD
- H =Hight of driver eys =1.2 m
- h =Hight of obstruction=1.2 m
5. On divided highways with four or more lanes, IRC suggests that it is not necessary to provide the OSD, but only SSD is sufficient.
6. The value of overtaking sight distance recommended by IRC is given as:
| Speed(mph) | Safe Overtaking Sight Distance (meters) |
| 40 | 165 |
| 50 | 235 |
| 60 | 300 |
| 65 | 340 |
| 80 | 470 |
| 100 | 640 |
7. Effect of Gradient on Overtaking Sight Distance
- IRC has not considered the effect of gradient for OSD calculation.
- On an ascending gradient, the overtaking sight distance required is more due to the reduced acceleration of overtaking vehicles, and vehicles coming from opposite directions are likely to speed up. The effect of the gradient is compensated by reducing the speed of the overtaken vehicle.
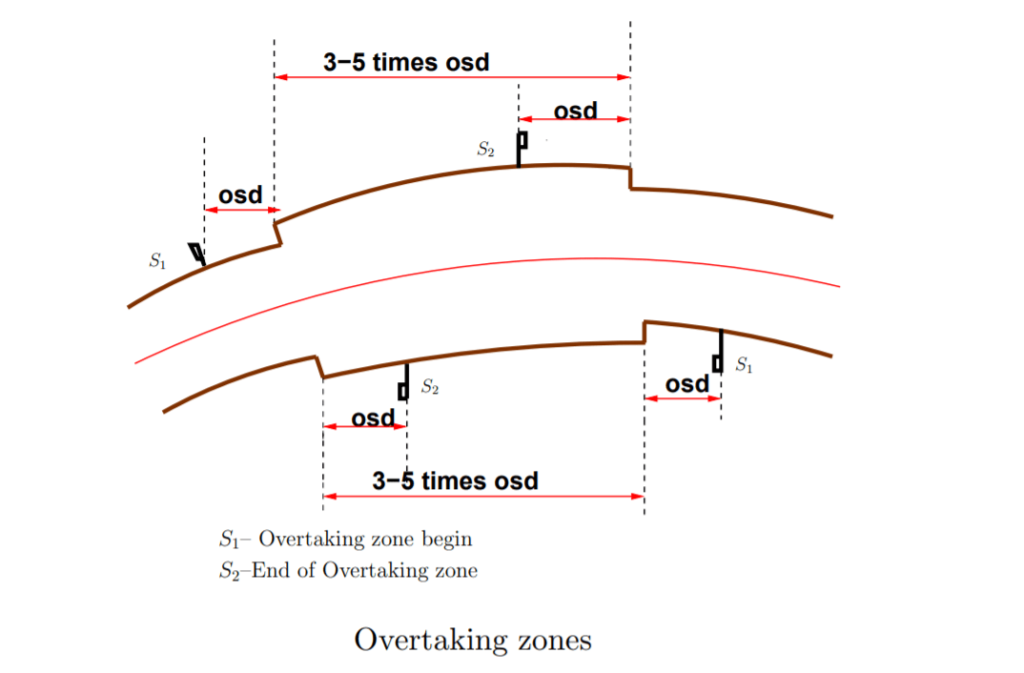
8. Overtaking Zones
Overtaking zones are provided when OSD cannot be provided throughout the length of the highway. These are zones dedicated to overtaking operations, marked with wide roads. The desirable length of overtaking zones is 5 time OSD and the minimum is 3 times OSD.
9. If the space head is not the same before and after overtaking the operation that
s1 +s2 + vB·T = vB•T+ \(\frac{1}{2}\)×a·T²
T= \(\sqrt{\frac{2(s_1+s_2)}{a}}\)
3. Intermediate Sight Distance (ISD)
On a horizontal curve, the requirement of overtaking sight distance can not always be satisfied. In such cases overtaking is prohibited by using regulatory signs. To provide an opportunity for overtaking operation on horizontal curves or in restricted areas, we provide intermediate sight distance, i.e. equal to twice of stopping sight distance.
SSD<ISD<OSD
Generally
ISD= 2×SSD
The measurement of the ISD may be made assuming both the height of the eye of the driver & height of the object to be 1.2m.
| Distance | Reaction Time (sec) | Height (meter) | |
| Driver Eye | Object | ||
| SSD | 2.5 | 1.2 | 0.15 |
| OSD | 2 | 1.2 | 1.2 |
| ISD | 2.5 | 1.2 | 1.2 |
| Space Headway | 0.7 | – | – |
Space Headway (s)
It is the distance between two consecutive vehicles traveling in the same direction.
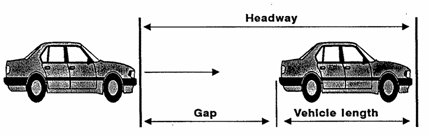
s= Gap+ l
for over safe Gap= SSD
s= SSD+l
s= LL +LB +l
here LB= 0 & l= 6-meter standard length of vehicle
s= 0.278×V×tr+6
s= 0.278×V×0.7+6. (tr=o.7 sec)
s= 0.1946V+6
As per IRC
s= 0.2V +6
s in meters, V in km/hr
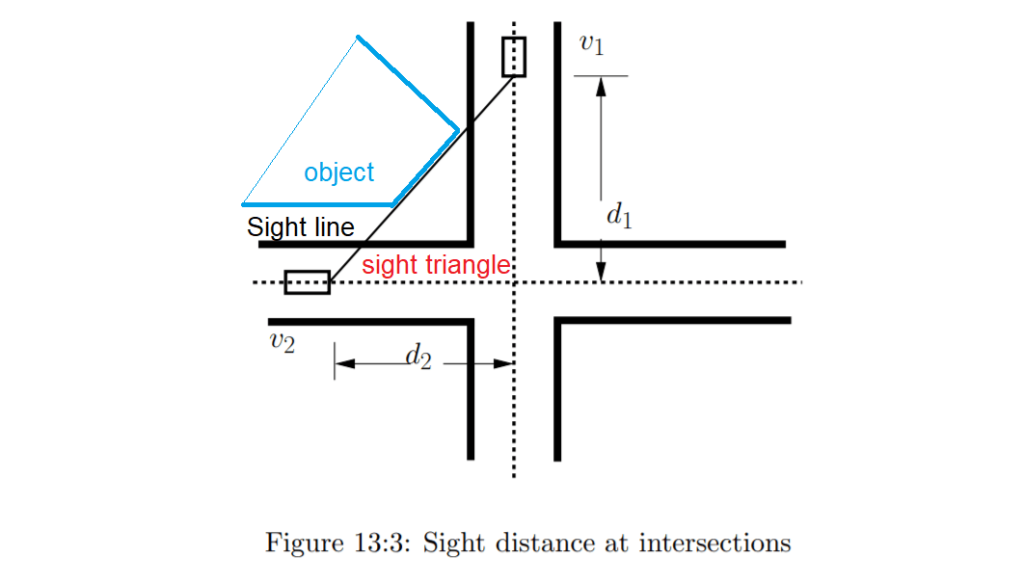
4. Sight distance at Intersections
At intersections where two or more road meets, clear views across the corners should be provided from a sufficient distance to avoid the collision of vehicles. The sight distance should be provided in such a way so that drivers from both sides can see each other. The area of unobstructed sight formed by the lines of vision is called the sight triangle as shown in
Design of sight distance at intersections may be used on three possible conditions:
• Enabling approaching vehicles to change the speed
• Enabling approaching vehicle to stop
• Enabling stopped vehicles to cross a main road
Curve
Curves are provided in highways in order that the change of direction at the intersection of straight alignments either in horizontal or vertical plane, shall be gradual.
The necessity of curves arises due to the following reasons:
- Topography of the country
- To provide access to a particular locality
- Restrictions imposed by property
- Preservation of existing amenities
- Avoidance of existing religious, monumental and other costly structures
- Making use of the existing right of way
Advantages of Curves
The advantages of providing curves are:
- They provide comfort to the passengers. If there is an abrupt change in the direction nor grade of a highway it will upset the passengers.
- They help to avoid mental strain induced by the monotony of continuous journey along straight path.
- In the case of sharp turns, brakes have to be applied more frequently which reduces the life of tyres. Thus life of the vehicles in increased by providing curves.
- The drivers became alert due to the change in the direction of road.
- They help to keep the speed of the vehicle within limits. On a straight road, a driver is tempted to go at a much faster speed.
Factors Affecting the Design of Curves
The various factors which affect the design of curves are:
- Design speed of the vehicle
- Maximum permissible superelevation
- Allowable friction
- Permissible centrifugal ratio
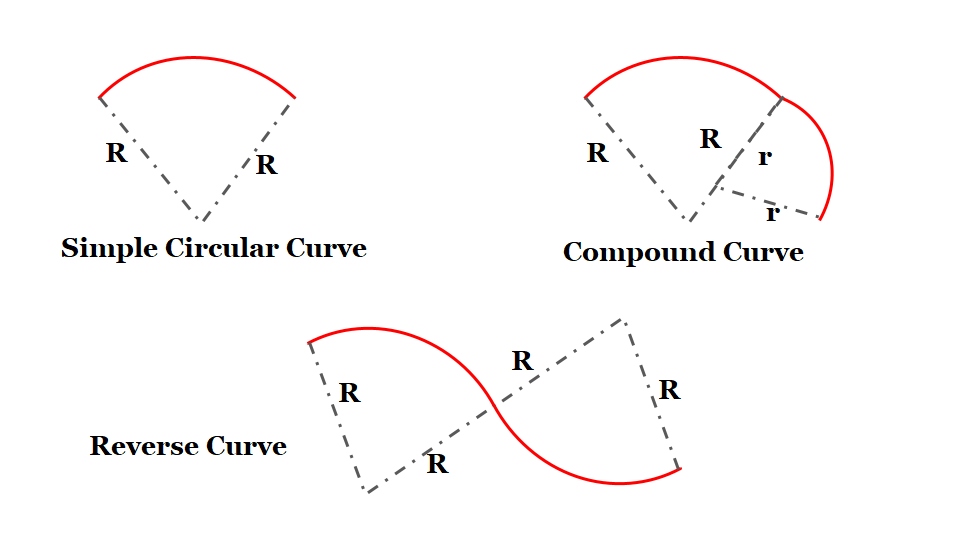
Type of Curves
Curves have been divided into two classes:
(1) Horizontal Curve: A curve in a plan to provide a change in direction of the central line of a road.
(ii) Vertical Curve: A curve in the longitudinal section of a roadway to provide for easy change of gradient.

The different types of curves used in highways are:
(i) Simple Circular Curve: A simple cùrve consists of a single area connecting two straights.
(ii) Compound Curve: A compound cùrve consists of a series of two or more simple curves that turn in the same direction and join at common tangent points.
(iii) Reverse Curve: A reverse cúrve consists of two simple curves of opposite direction that join at the common tangent point called the point of reverse curve.
Design of Horizontal Alignment:
Various design elements to be considered in the horizontal alignment are:
- Design Speed
- Horizontal Curve
- Superelevation
- Radius of Curve
- Width of Pavement- ExtraWidening, Off Tracking
- Transition Curve- Type and Length of Transition Curve
- Set back distance
Design Speed
- The design speed is the main factor on which most of the geometric design element depends including horizontal elements.
- The design is the speed of the road depends, upon the class of road and terrain.
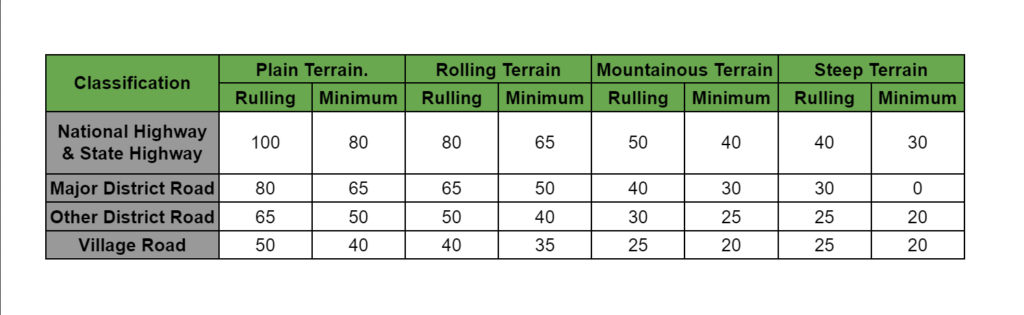
- Classification of terrain & design speed for different classes of road is as follows:


- Design speeds are also being defined for urban roads.
- Two values of speed ruling and minimum are being specified for each type of Road.
- As far as possible, an attempt must be made to design all the geometric elements for ruling speed however site conditions and economic considerations do not permit so, the design must be done for minimum design speed.
Horizontal Curve
Stability Analysis on Horizontal Curve without Superelevation
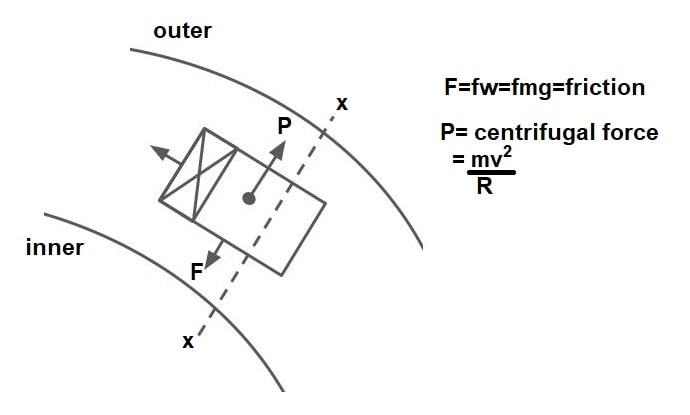
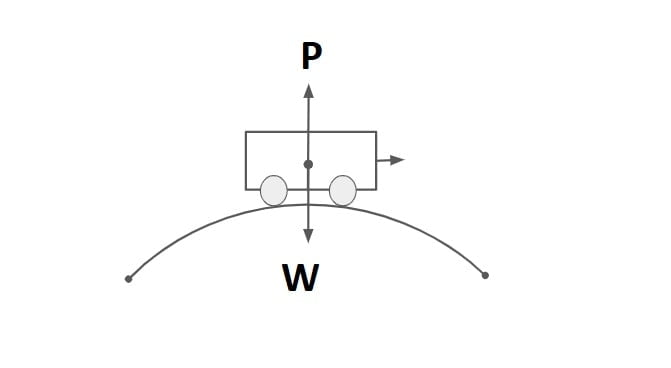
It is the curve in the plane to provide a change in the direction to the Central line on the road. When a vehicle travels on a horizontal curve, the centrifugal force acts horizontally outward through the center of gravity of the vehicle.
The centrifugal force depends upon the speed of the vehicle and the radius of the horizontal curve.
It will be counteracted by lateral /transverse friction developed between the tire & pavement, which helps the vehicle to change direction along the curve.
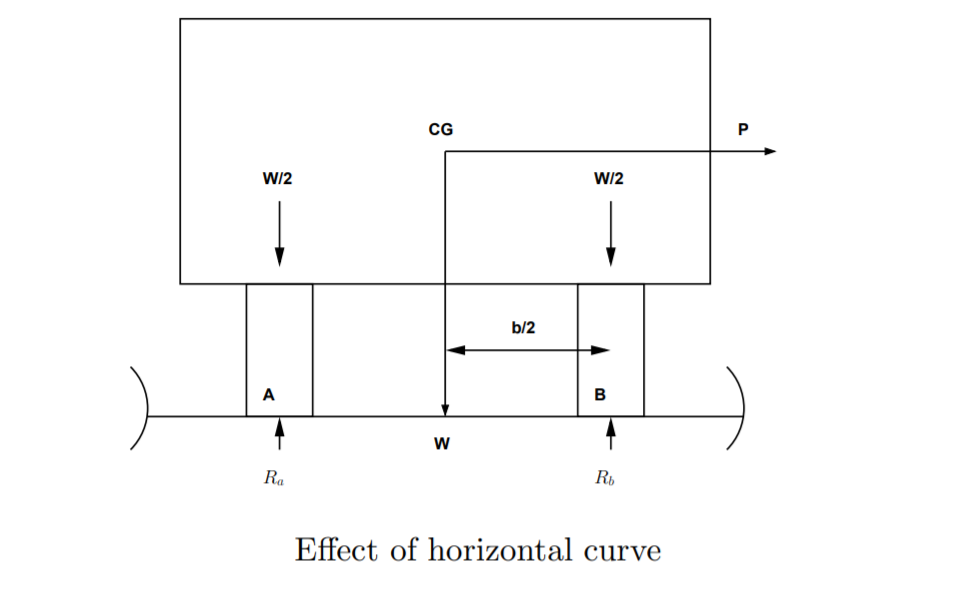
They are the centrifugal force (P) acting outward, the weight of the vehicle (W) acting downward, and the reaction of the ground on the wheels (RA and RB). The centrifugal force P in Newton is given by
\(P=\frac{mv^{2}}{R}\)where m is the mass of the vehicle in kg, v is the speed of the vehicle in m/sec, g is the acceleration due to gravity in m/sec2 and R is the radius of the curve in m. The centrifugal ratio or the impact factor \(\frac{P}{W}\) is given by:
\(\frac{P}{W}=\frac{\frac{mv^{2}}{R}}{mg}=\frac{v^{2}}{gR}\)
The force acting on the vehicle tends to either Overturning the Vehicle outward about wheels & to Skid the Vehicle laterally outward.
1. Overturning the vehicle
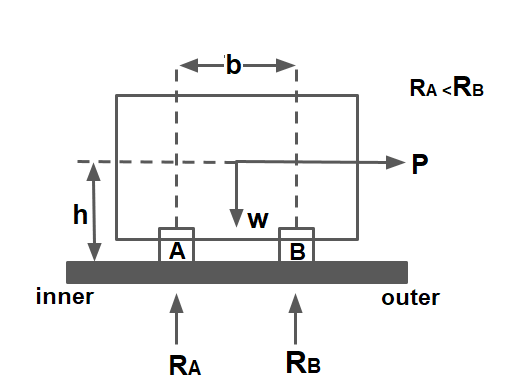
Overturning Moment MO= P×h
Resistive Moment MR= W×\(\frac{b}{2}\)
Case.1 To avoid overturning:
MO < MR
P×h< W×\(\frac{b}{2}\)
I= \(\frac{P}{W}<\frac{b}{2h}\)
Case.2 On the verge of overturning:
MO = MR
P×h= W×\(\frac{b}{2}\)
I= \(\frac{P}{W}=\frac{b}{2h}\)
Case.3 Unsafe case:
MO > MR
P×h> W×(b/2)
I= \(\frac{P}{W}>\frac{b}{2h}\)
2. Lateral Skidding of the Vehicle
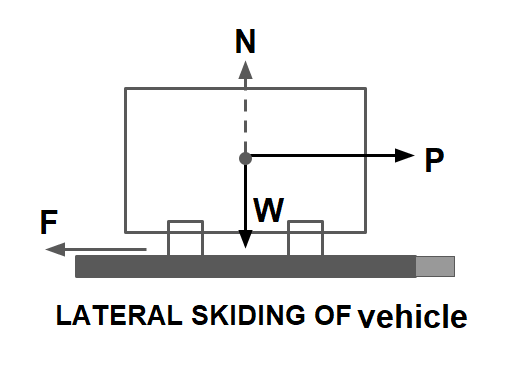
Skiding Force= P= \(\frac{mv²}{R}\)
Resistive Force= F= f·W= f·m·g
Case.1 To avoid skidding:
P< f×W
I= \(\frac{P}{W}<f\)
Case.2 On the verge of skidding:
P= f×W
I= \(\frac{P}{W}=f\)
Case.3 Unsafe case:
P> f×W
I= \(\frac{P}{W}>f\)
Note:
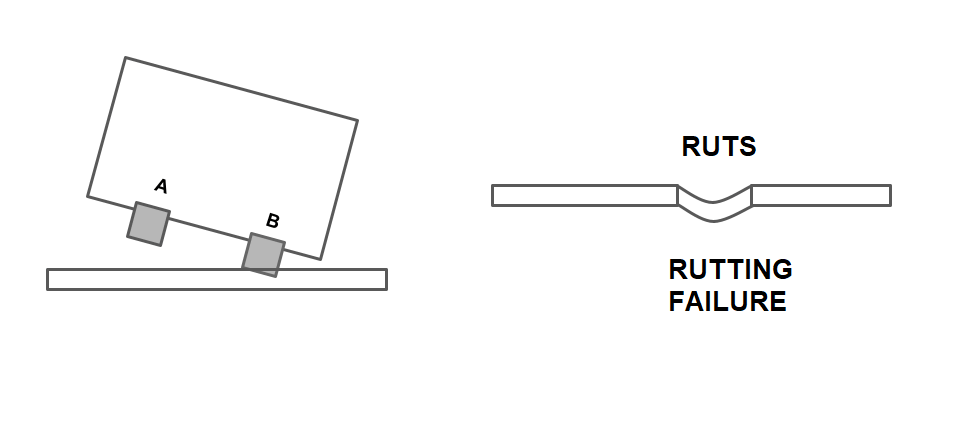
- If the pavement is kept horizontal across the alignment, The pressure on the outer will be higher due to centrifugal force acting outward direction.
- When the limiting equilibrium condition for overturning occurs, the pressure at inner wheel becomes zero.
- Since the pressure on the outer wheel is comparatively greater, it damages the pavement by developing ruts over it. RUTTING FAILURE
Hence to avoid both overturning & sliding :
\(I=\frac{P}{W} \leq\left\{\begin{array}{c}
\frac{b}{2 h} \\
and \\
f
\end{array}\right.\)
The relative dangerous of lateral skidding and overturning depends upon weather ‘f’ is lower or higher than \(\frac{b}{2h}\).
If
f< \(\frac{b}{2h}\)⇒ Transverse of skidding before overturning.
f> \(\frac{b}{2h}\)⇒ Overturning before transverse skidding.
Superelevation
The transverse inclination throughout the length of the horizontal curve by raising outer edge counteract w.r.t. inner edge, in order to counteract the effect of centrifugal force is known as superelevation (or cant or banking).
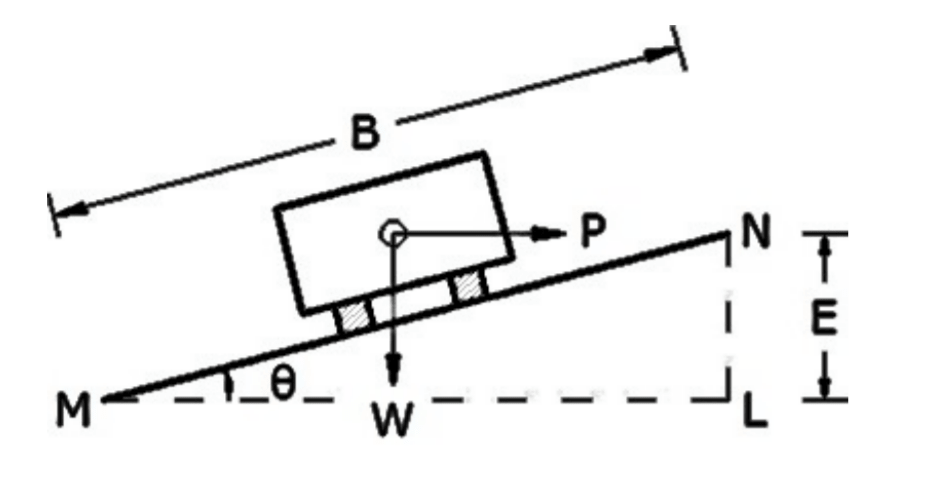
The superelevation ‘e’ is expressed as the ratio of height of outer edge w.r.t. the horizontal width, i.e
Superelevation (e)= \(\frac{NL}{ML}\)
e= tanθ
θ is very small and the value of tanθ ⊁ 0.007 (7%)
e= tanθ ≅ sinθ = \(\frac{E}{B}\)
Analysis for Expression of Super-elevation
Consider a vehicle moving at a speed of v m/s on a circular curve having radius ‘R’.
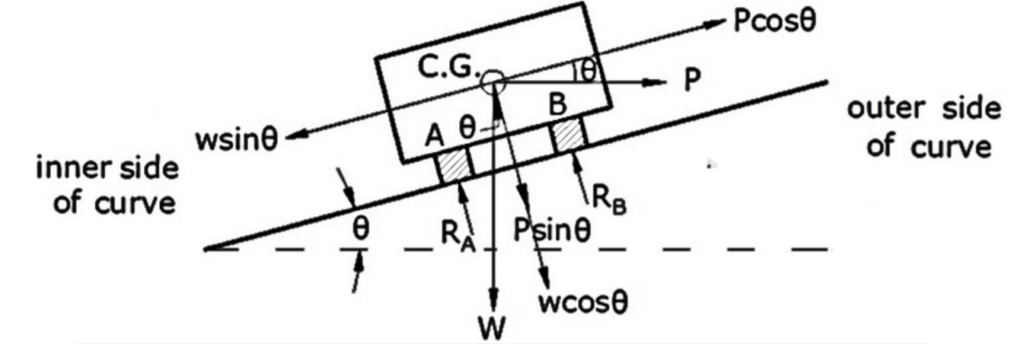
The following forces acting on the vehicle:
i) Centrifugal force (P) acting horizontally through the center of gravity (CG) of vehicle
P= \(\frac{mv²}{R}=\frac{W·v^{2}}{gR}\) ——-(1)
ii) The weight (W) of the vehicle action vertically downwards through the C.G. of the vehicle
iii) The frictional force (FA & FB) developed between the wheels and pavement, transversely along the pavement surface.
FA =RA ×f and FB =RB ×f ——-(2)
where
RA and RB = frictional resistance between wheel and pavement
f = coefficient of lateral friction
Considering equilibrium, the component of centrifugal force parallel to the pavement (Pcosθ) is opposed by component of weight parallel to the pavement and frictional force FA and FB,
P cosθ= W sinθ + (FA + FB )
P cosθ= W sinθ + f(RA + RB )
P cosθ= W sinθ + f(P sinθ+ W cosθ )
P(cosθ- sinθ)= W(sinθ +fcosθ)
\(\frac{\mathrm{P}}{\mathrm{W}}=\frac{\sin \theta+f \cos \theta}{\cos \theta-f \sin \theta}\)
dividing by cosθ on right side term
\(\frac{\mathrm{P}}{\mathrm{W}}=\frac{\tan \theta+f }{1-f \tan \theta}\).
from equation 1 \(\frac{P}{W}=\frac{v^{2}}{gR}\).
\(\frac{v^{2}}{gR}=\frac{tan\theta +f}{1-ftan\theta}\).
tanθ=e
\(\frac{v^{2}}{gR}=\frac{e+f}{1-ef}\).
Here, Coefficient of lateral friction ( f ) = 0.15
Maximum value of super-elevation (tanθ) = 0.07 (7 %)
1-e·f= 0.99≅ 1 (As per IRC)
hence
e+f=\(\frac{v^{2}}{gR}\) , v in m/sec
Here, e = rate of super-elevation = tanθ
If the speed of vehicle is represented as V kmph then
Formula for Superelevation
e+f=\(\frac{V^{2}}{127R}\) , V in km/h
Note: For Racing Track
\(\frac{e+f}{1-ef}= \frac{v^{2}}{Rg}\), v in m/sec
Equilibrium Superelevation
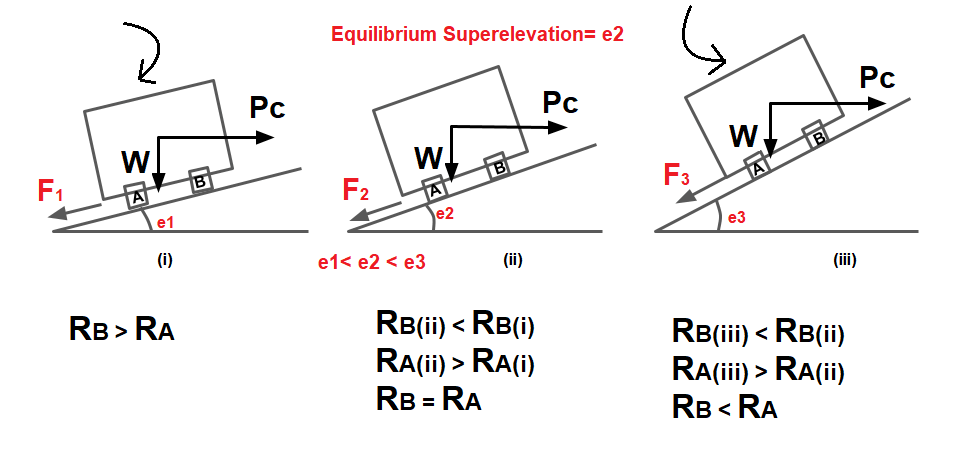
Equilibrium superelevation is the superelevation at which pressure at the inner and outer tire will be equal. if the coefficient of friction is neglected i.e. f =0 then,
e=\(\frac{V^{2}}{127R}\) , V in km/h
This means that if a road surface is super elevated by tan-1\(\frac{V^{2}}{127R}\) then the friction force will not be called upon to act and thus the pressure on both the wheel will be equal.
eequilibrium =\(\frac{V^{2}}{127R}\)
If the superelevation provided is less than eequilibrium lateral fiction will come into play and will go on increase as the superelevation gets reduced.
Note⇒ Due to equilibrium superelevation:
- No overturning, No Toppling, No Skidding, No Sliding.
- Pressure at the inner and outer tyre will be equal.
Superelevation As Per IRC
1. Maximum Superelevation
| Type of Road | Maximum Superelevation (emax) |
| Urban Road | 4% or 0.04 |
| Plain & Rolling Terrain | 7% or 0.07 |
| Mountainous & Steep Terrain | 10% or 0.10 |
2. The minimum superelevation
It is provided on a road must not be less than the camber of the road for the adequate drainage of water from the surface.
Design of Superelevation
The design of superelevation is a complex problem for mixed traffic conditions because different vehicles are moving with different speeds hence the required superelevation is also different.
In this case, IRC suggests designing the superelevation for 75% of the design speed considering coefficient of friction is 0.
Step.1: The super elevation is calculated for 75% of design speed, neglecting the lateral friction.
e+f=\(\frac{V^{2}}{127R}\), V in km/h
for design, f=0, V=0.75V.
e =\(\frac{(0.75V)^{2}}{127R}\).
e =\(\frac{V^{2}}{225R}\).
Step.2: If the calculated value of ‘e’ is less than 7%, so obtained ‘e’ is provided. If the value of ‘e’ is more than 7%, then provided e= emax (7%) check for lateral friction also
Step.3: Check for friction developed for maximum value of e=7% at full value of design speed.
e+f=\(\frac{V^{2}}{127R}\).
f=\(\frac{V^{2}}{127R}\)-e.
f=\(\frac{V^{2}}{127R}\)-0.07.
If the value of ‘f’ calculated is less than 0.15, the superelevation of 7% is safe for the design but if it comes out to be more than 0.15, then if speed of vehicle has to the restricted to safe value. which is less than design speed.
Step.4: The allowed level speed at the car peach computed as follows
e+f= \(\frac{V^{2}}{127R}\).
0.07+0.15= \(\frac{V_A^{2}}{127R}\).
VA =5.25\(\sqrt{R}\)
- If the allowable speed is higher than design speed then the design speed is adequate but it is less than design speed, the speed is limited to the allowable speed.
- Speed can be reduced by warning signs of yi speed limit regulations sign.
- On important highways as for as possible speed is not reduced hence the curve should be realigned with a larger radius of curvature.
Method of Obtaining Superelevation
Introducing superelevation on a horizontal curve in the field is an important feature in construction. The full super-elevation is attained by the end of transition curve or at the beginning of the circular curve.
The attainment of superelevation may be split up into two parts:
- Elimination of the crown of the cambered section
- Rotation of pavement to attain full superelevation
i) Elimination of the crown of the cambered section
This may be done by two methods:

Method 1
In this method, the outer half of the cross-slope is rotated about the crown at a desired rate such that the surface falls on the same plane as the inner half and the elevation of the center line is not altered.
The outer half of the cross-slope is brought to level or horizontal at the start of the transition curve or at tangent point (T.P.). Subsequently, the outer half is further rotated to obtain a uniform cross-slope equal to the camber.
This method has a drawback that the surface drainage will not be proper at the outer half.
Method 2
In this method, the crown is progressively shifted outwards, thus increasing the width of the inner half of cross-section progressively. This method is not usually adopted as a portion of the outer half of the pavement has increasing value of negative super-elevation.
ii) Rotation of pavement to attain full super-elevation
When the crown of the camber is eliminated, It does not signify that the superelevation desired at that section is attained. If the desired superelevation is more than camber/ cross sections the payment section will have to be rotated for till the desired superelevation is attained.
Desire superelevation can be attained by two methods:

Method 1
By rotating the pavement cross section about the centre line, depressing the inner edge & raising the outer edge each by half the total amount of superelevation required with respect to centre.
Method 2
By rotating the pavement cross section about the inner edge of the pavement raising both centre as well as the outer edge of the pavement such as the outer edge is raised by the full amount of superelevation desired.
| Rotation about center line | Rotation about inner edge |
| It may with interfere drainage system. | No interference with drainage system. |
| Centre line remain unchanged. | Centre line is elevated. |
| Earth work is balanced in cutting & filling. | Filling is required. |
In cases where a transition curve cannot be provided for some reason, 2/3 of superelevation may be attained at the straight portion before the start of the circular curve and the balance 1/3 is provided at the beginning of the circular curve.
The superelevation is introduced by raising the outer edge of the pavement at a rate not exceeding (1 in 150) in plain & rolling terrain and (1in 60) in mountainous & steep terrain.
Radius of Horizontal Curve
Horizontal curves of highways are designed for the specified design speed (Ruling & Min).
However, if this is not possible due to site restriction, the horizontal curve may be redesigned.
Based on the speed Radius of the Horizontal Curve is classified into the following:
1. Ruling Minimum Radius(RMR)
e+f=\(\frac{V^{2}}{127R}\).
RMP=\(\frac{V^{2}}{127(e_{max}+f)}\).
V= Ruling design speed (kmph)
2. Absolute Minimum Radius(AMR)
e+f=\(\frac{V’^{2}}{127R}\).
AMR=\(\frac{V’^{2}}{127(e_{max}+f)}\).
V’= Ruling design speed (kmph)
3. Radius beyond which no superelevation is required (RBNSN)
It is the radius, corresponding to which camber serve the purpose of superelevation.
e+f=\(\frac{V^{2}}{127R}\).
e=camber, f=0, V=0.75V
camber=\(\frac{{0.75V}^{2}}{127R}\).
RBNSN=\(\frac{V^{2}}{225×camber}\).
ExtraWidening
Extra width provided to the Road at a horizontal curve is called extra widening.
It is provided for the following purposes:
- To avoid off-tracking due to the rigidity of wheelbase.
- To encounter the psychological tendency of the driver.
- To increase visibility at the curve.
- To account for lateral skidding.
Off tracking
The path traveled by the front axle and the path traveled by the rear axle it is not the same on a horizontal curve this phenomenon is called off-tracking.
Extrawidening is split up into two parts:
- Mechanical widening
- Psychological widening
WE= WM+WP
WE= Extra widening
WM =Mechanical widening
WP= Psychological widening
(i) Mechanical widening:
Mechanical widening is provided to account for tracking.
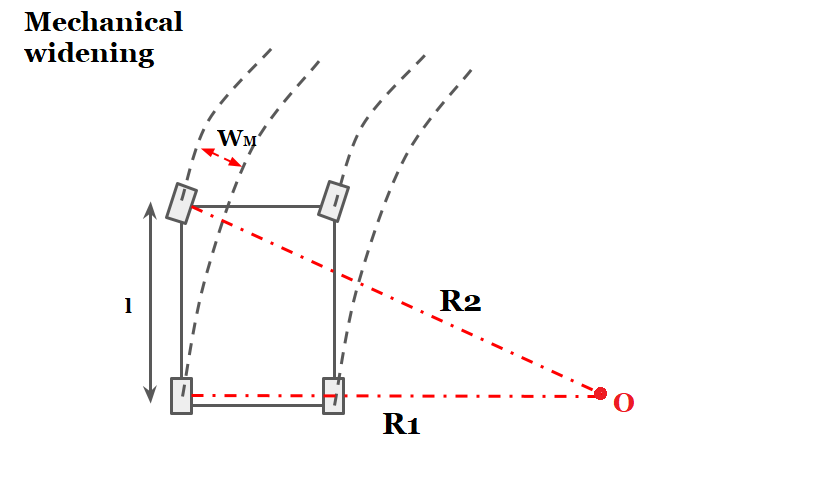
R₁ = Radius of path traversed by the outer rear wheel (in m) wheel (in m)
R2 = Radius of path traversed by the outer front wheel (in m)
l = Length of wheel base (in m)
WM = Mechanical widening (in m)
\(R_2^{2}=R_1^{2}+l^{2}\).
\(R_2^{2}=(R_2-W_M)^{2}+l^{2}\).
\(R_2^{2}=R_2^{2}-2R_2W_M+W_M^{2}+l^{2}\).
\(2R_2W_M-W_M^{2}=l^{2}\).
\(W_M=\frac{l^{2}}{2R_2-W_M}≅\frac{l^{2}}{2R}\). where, R= mean radius of curve.
\(W_M=\frac{l^{2}}{2R}\).
Now for ‘n’ lane Road
\(W_M=\frac{nl^{2}}{2R}\).
(ii) Psychological widening:
There is a psychological tendency of driver to drive the vehicle close to the edge of pavement and maintain more side gap between the vehicle moving parallely.
\(W_P=\frac{V}{9.5\sqrt{R}}\).
Where WP in m, R in m, V in KMPH.
WE= WM+WP
WE= \(\frac{nl^{2}}{2R}\)+\(\frac{V}{9.5\sqrt{R}}\).(extra widening formula)
Note
IRC recommended value of extra widening for single and tow lane pavement are given below.
For single lane road Psychological widening =0.
If R> 300 m, then extra widèning is not provide.
If R< 50 m, then extra widèning is provided at inner edge.
If 50<R<300 m, then extra widèning is provided at both the edge.
Transition Curves
When a vehicle traveling on a straight road enters into a horizontal curve instantaneously, it will ca discomfort to the driver. To avoid this, it is required to provide a transition curve. This may be provided either between a tangent and a circular curve or between two branches of a compound or reverse curve.
The transition curve has a radius equal to infinite when it meets to straight Road within gradually change to designate radius towards the circular curve.
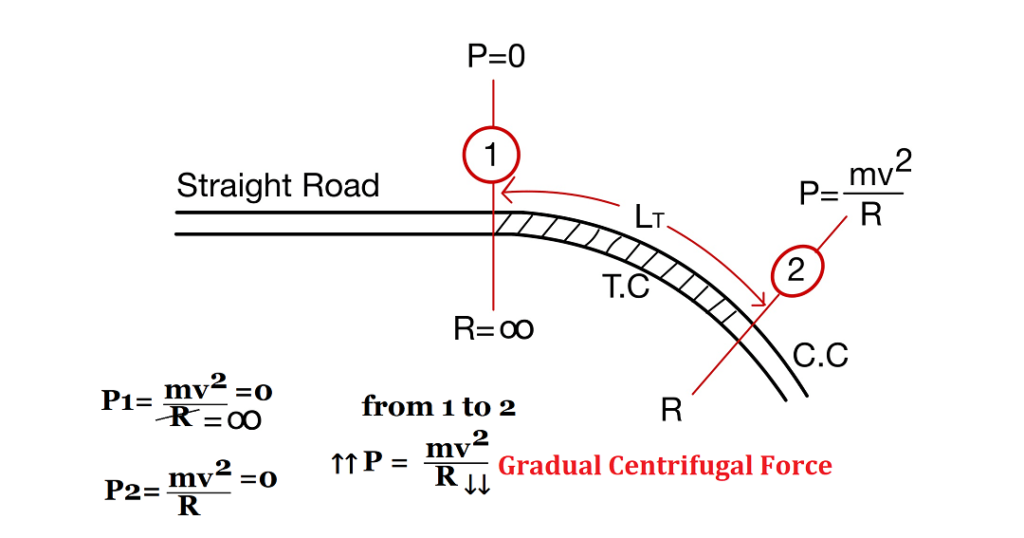
The objectives of providing transition curves are:
- To gradually introduce the centrifugal force between straight and circular curves.
- To avoid the certain jerk.
- To gradual introduction of superelevation and extra widening.
- To enable the driver turn the sheering gradually for comfort and security.
- To improve aesthetic appearance.
A transition curve should satisfy the following conditions
- It should meet the straight path tangentially.
- It should meet the circular curve tangentially.
- It should have the same radius as that of the circular curve at its junction with the circular curve.
- The rate of increase of curvature and superelevation should be the same.
The length of the transition curve required on a horizontal highway curve depends upon the following factors:
- The radius of the circular curve, R
- Design speed, V
- Allowable rate of change of centrifugal acceleration, C
- Maximum amount of superelevation, E which depends on the maximum rate of superelevation, e and the total width of the pavement, B at the horizontal curve.
- Rotation of pavement cross-section either about the inner edge or the centre line
Different Types of Transition Curves
The types of transition curves commonly adopted in horizontal alignment of highways are:
1. Spiral
2. Bernoulli’s Lemniscate
3. Cubic Parabola
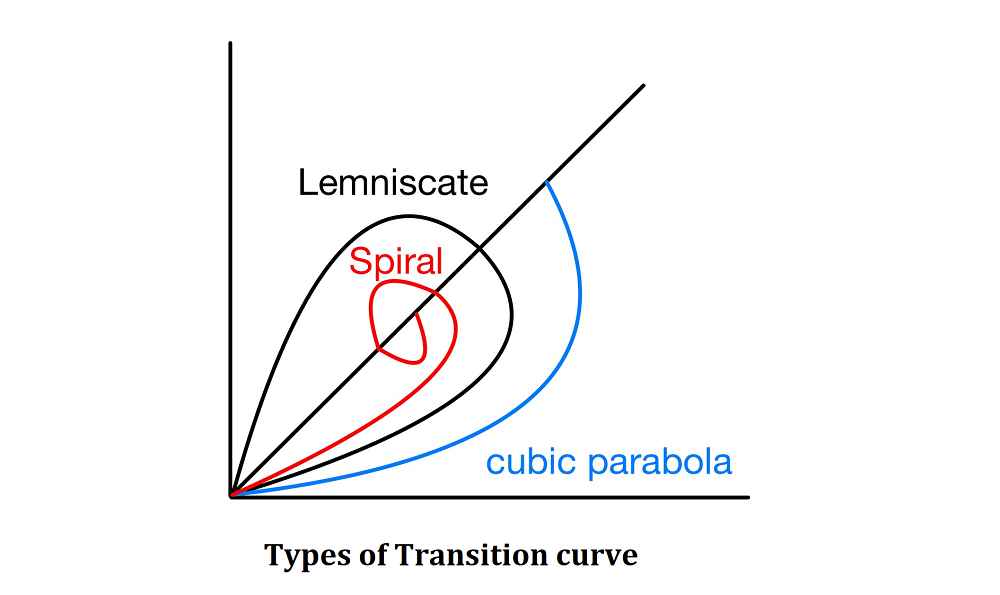
NOTE:
- In all these curves the radius decreases as the length increases.
- But the rate of change of radius or rate of change of centrifugal force is not constant in case of Lemniscate and cubic parabola.
- Hence a spiral curve is used as transition curve as it fulfills the requirement of ideal transition curve.
- According to IRC an ideal transition curve is spiral because rate of change of radial acceleration (C) remains constant.
Length of Transition Curve
The length of the transition curve is designed to fulfill three conditions:
- The rate of change of centrifugal acceleration to be developed gradually
- Rate of introduction of the designed superelevation to be at a reasonable rate, and
- Minimum length by IRC empirical formula
The length of the transition curve following three conditions:
1. Length of Transition Curve by the Rate of Change of Radial Acceleration
The length of the Transition Curve is designed such that the rate of change of centrifugal force is low.
Rate of change of centrifugal acceleration:
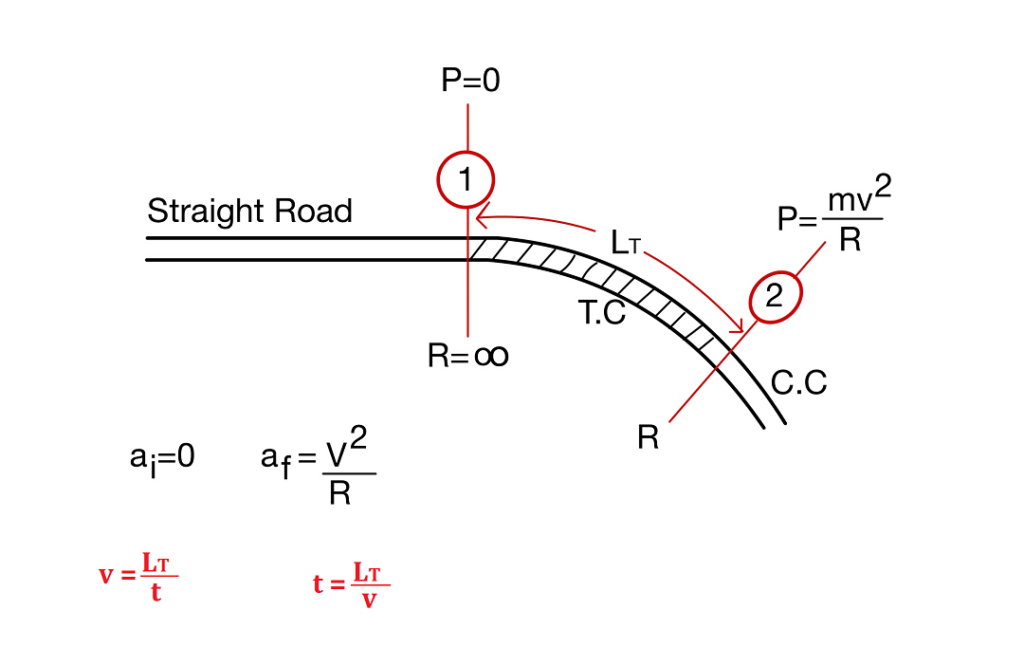
v=Velocity of the vehicle in m/s | R= Radius of the curve in m |
C= rate of change of radial acceleration in m/sec3 | LT= Length of Transition Curve in m |
t= time taken by vehicle in second to travel the transition length at speed v. | |
\(C=\frac{\Delta a}{T}=\frac{a_f-a_i}{T}\).
\(C=\frac{\frac{v^{2}}{R}-0}{\frac{L_T}{v}}=\frac{v^{3}}{R·L_T}\).
\(C=\frac{v^{3}}{R·L_T}\).
| \(L_T=\frac{v^{3}}{C·R}\) | (Here,v in m/s) |
or | |
\(L_T=\frac{0.0215V^{3}}{C·R}\) | (Here,V in km/s) |
The rate of change of centrifugal acceleration is given by an empirical formula recommended by IRC
Subject to a maximum of 0.8 and minimum of 0.5.
2. Length of Transition Curve by Rate of Change of Superelevation
Rate of introduction if superelevation = 1-Vertical in N-Horizontal
1= elevation provided
N= Length of Transition curve
Rate As per IRC
| 1:150 For Plain and Rolling terrain | 1:100 For Urban /Built Up Area | 1:60 For Hilly Area |
The length of transition curve = N·x
where x is elevation of outer edge.
(i) When pavement is rotated about the inner edge
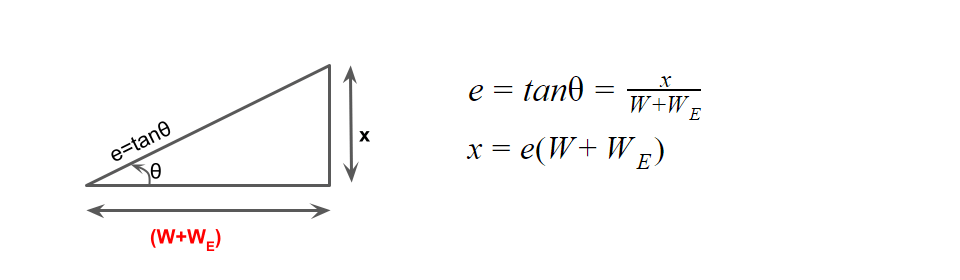
LT=eN(W+WE)
W=Width of pavement
WE= Extra widening
(ii) When pavement is rotated about centre
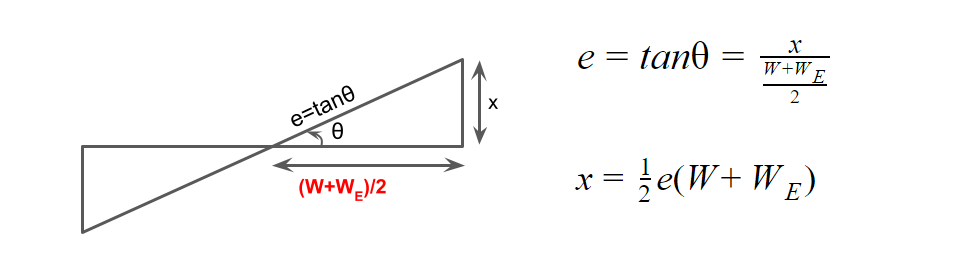
LT=\(\frac{1}{2}\)eN(W+WE)
3. Empirical Formula for the Length of Transition Curve Recommended by IRC
Setting Out of Transition Curve
When a Transition curve is introduced between a straight and circular curve, then the circular curve has to be shifted so that the transition curve meets the circular curve tangentially. The shift (S) of a circular curve is given by
note: incomplete
Set Back Distance
It is clearance distance, required from the centre line of pavement/road to the obstruction in ode to maintain the adequate sight distance to the curve.
The set back distance or clearance required from the centre line of horizontal curve depends upon.
- Required sight distance (SD)
- Radius of horizontal Curve (R)
- Length of curve(LC)
Calculation Of Setback Distance
There are two cases in the calculation of setback distance:
Case 1: When the length of horizontal curve greater than the sight distance (LC>SD).
(a) For Single Lane:
In single lane road the sight distance is measured along the centreline of the road.
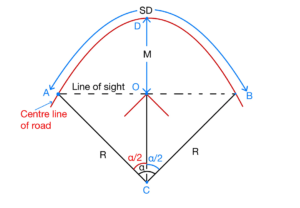
(b) For Multi lane:
In multi lane road the sight distance is measured along the centreline of the inner lane and the set back distance is measured from the centre of road.
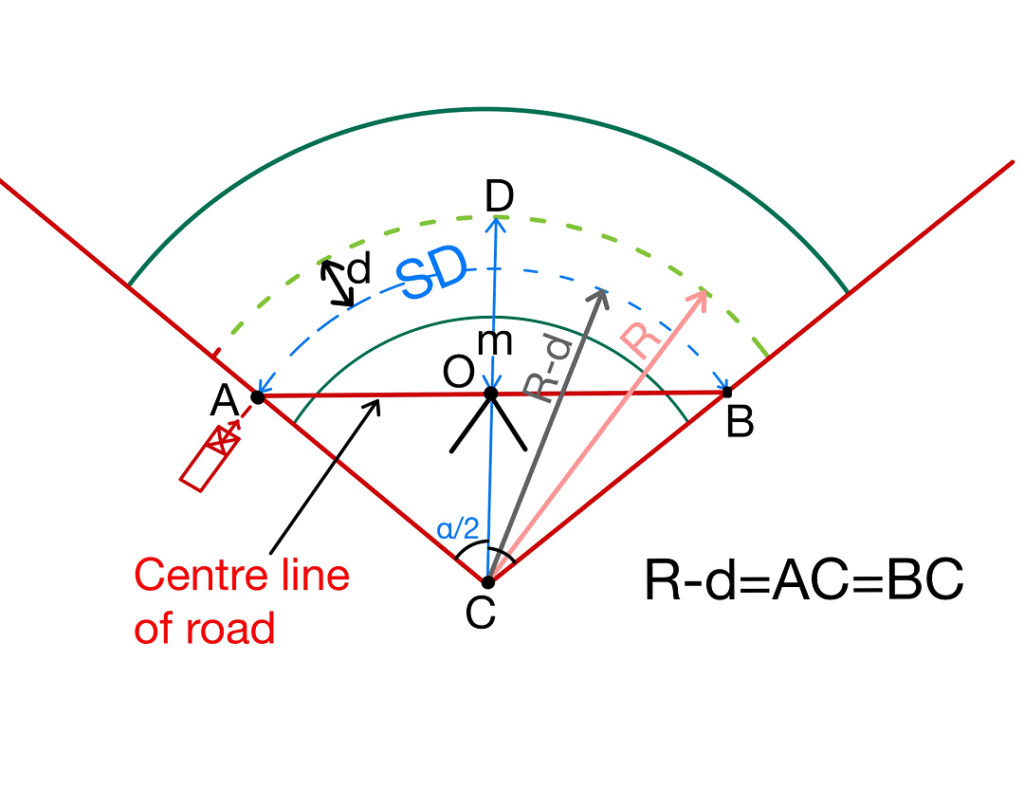
Let “d” be the distance between the centre line of road & centre line of the inside lane.
Case 2: When the length of horizontal curve less than the sight distance (LC<SD).
(a) For Single Lane:
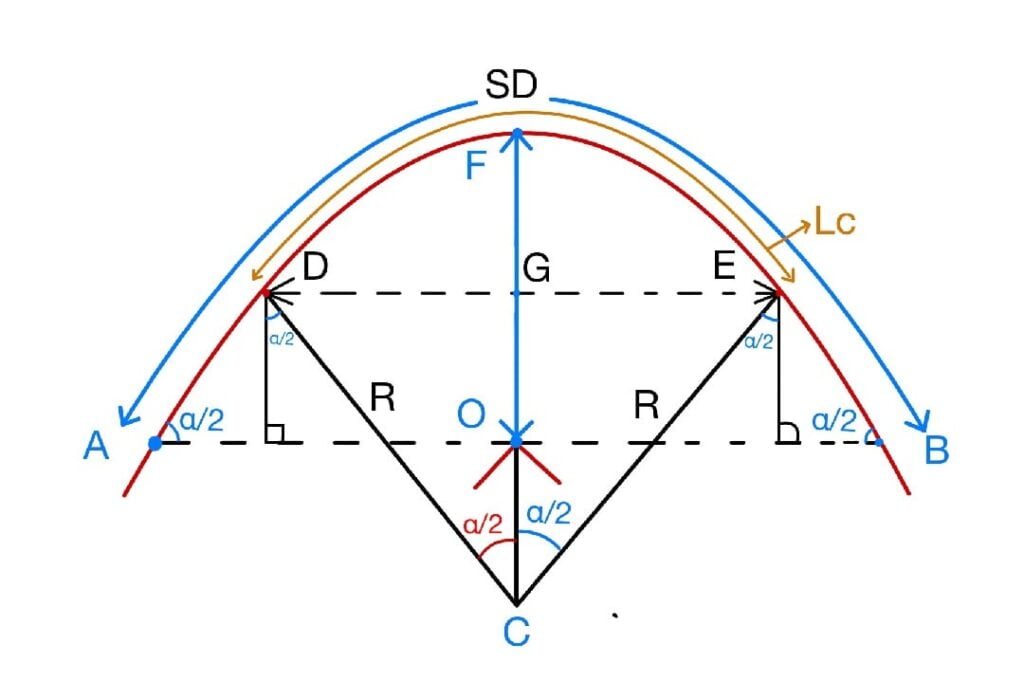
(b) For Multi lane:
\(m=R-(R-d)· cos\frac{\alpha }{2}\)+(\(\frac{SD-L_C }{2}\))\(sin\frac{\alpha }{2}\)
Here
\(\frac{\alpha }{2}=\frac{L_C}{2(R-d)}(Radians)\)
OR
\(\frac{\alpha }{2}=\frac{180}{\Pi }\frac{L_C}{2(R-d)}(Degrees)\)
Note:
Sēt back distance from central line of inner lane= m-d.
Sēt back distance from centre line of outer lane= m+d.
Sēt back distance from central line of inner edge= m-2d.
Sēt back distance from centre line of outer edge= m+2d.
In all the above case, a lane road is considered.
Design of Vertical Alignment
Generally Highway is aligned to follow the natural topography keeping in view the drainage and other design consideration.
The vertical alignment of a highway affects:
- Acceleration & Deceleration
- Operational cost of vehicle
- Sight distance
- Vehicle speed
The vertical alignment consists of two elements:
1. Gradient | 2. Vertical curve |
Gradient
It is designed as a change in elevation/height of the road along the length or may be defined as a rise or fall along the length of the road with respect to horizontal.
Slope due to a gradual rise or gradual fall in the direction of vehicle movement is called a gradient.
If it is a gradual rise then the slope is called an ascending /rising /positive gradient.
If it is a gradual fall then the slope is called a descending/ falling/negative gradient.
It can be represented as follows:
- 1 in x (1 vertical to x horizontal)
- \(\frac{1}{x}\times 100%\)
- tanα
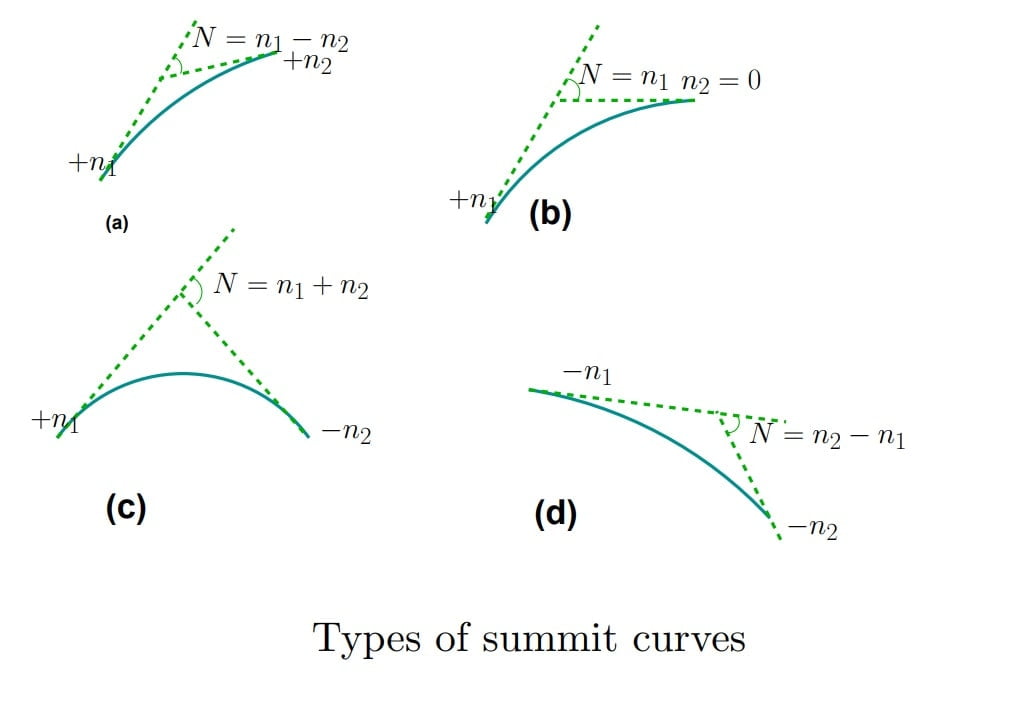
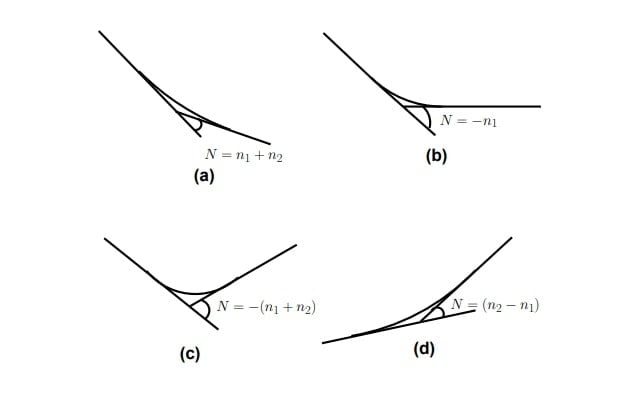
Note: The angle that measures the change in direction at the intersection of two grades is called as deviation angle.
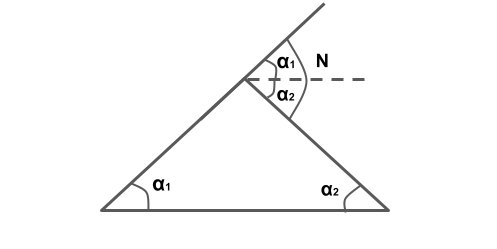
N= α1+α2
or N=α1-(-α2)
Type of Gradients
Gradients are divided into following types.
- Ruling Gradient
- Limiting Gradient
- Exceptional Gradient
- Minimum Gradient
Ruling Gradient:
It is the maximum gradient within which designer wants to design the vertical profile of the road, hence it is also known as design gradients. It depends upon topography, length of the grade, design speed, pulling power of vehicle and presence of horizontal curves.
Limiting Gradient:
It is steeper than ruling gradient and it is provided only when there is an enormous increase of cost of construction with ruling gradient. On rolling and hilly terrain, limiting gradient may be frequently adopted but the length of limiting gradient stretch should be restricted.
Exceptional Gradient:
It is steeper than ruling gradient and limiting gradient and provided only, if the situation is unavoidable. Length of exceptional gradient stitch should not be more than 100 m.
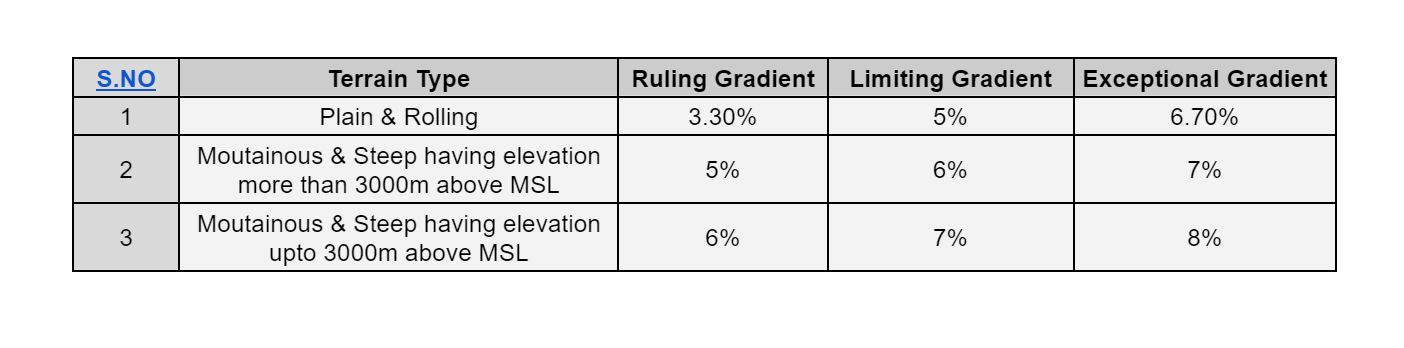
Minimum Gradient:
It is provided along the length of the road for a drainage point of view. The minimum gradient for cement concrete drain is 1 in 500.
As per IRC minimum gradient is as follows:
| Concrete drainage | 1/500 |
| Kutcha open drainage / Soil drainage | 1/ 200 |
Note: Depending upon the type of soil it can be taken up to 1/100.
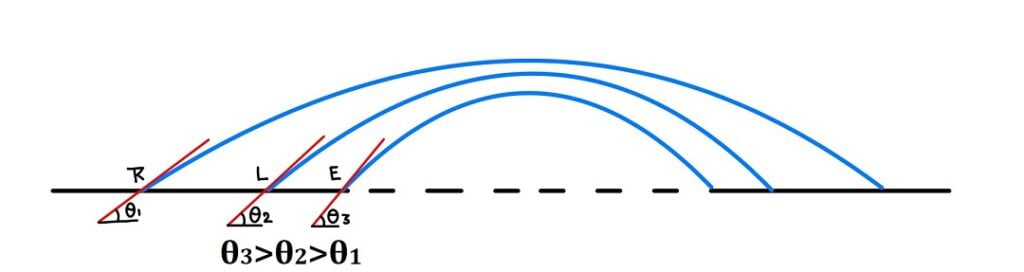
Steeper ⇒ EG>LG>RG>MG
Note: Grade Compensation at Horizontal Curves
When there is a horizontal curve in addition to gradient then there will be increased resistance to traction due to both curve and gradient. Therefore it is necessary to reduce in gradient at the horizontal curve.
This reduction in gradient at the horizontal curve is termed as “Gradient Compensation“, which is given by
GC%=\(\frac{30+R}{R}\)
R= Radius of horizontal curve
Grade compensation as taken is minimum of \(\frac{30+R}{R}\)% or \(\frac{75}{R}\)%, where ‘R’ is the radius of curve in metres.
Compensated gradient =Gradient-Grade compensation
NOTE:
According to IRC grade compensation is not necessary for the gradient flatter than 4%.hence it is not being provided beyond (less than) 4%.
Vertical Curve
Vertical Curves are provided at the intersections of different grades to smoothen the vertical profile.
The vertical curves used in the highway are of two types
- Summit Curve
- Valley Curve
Summit Curve
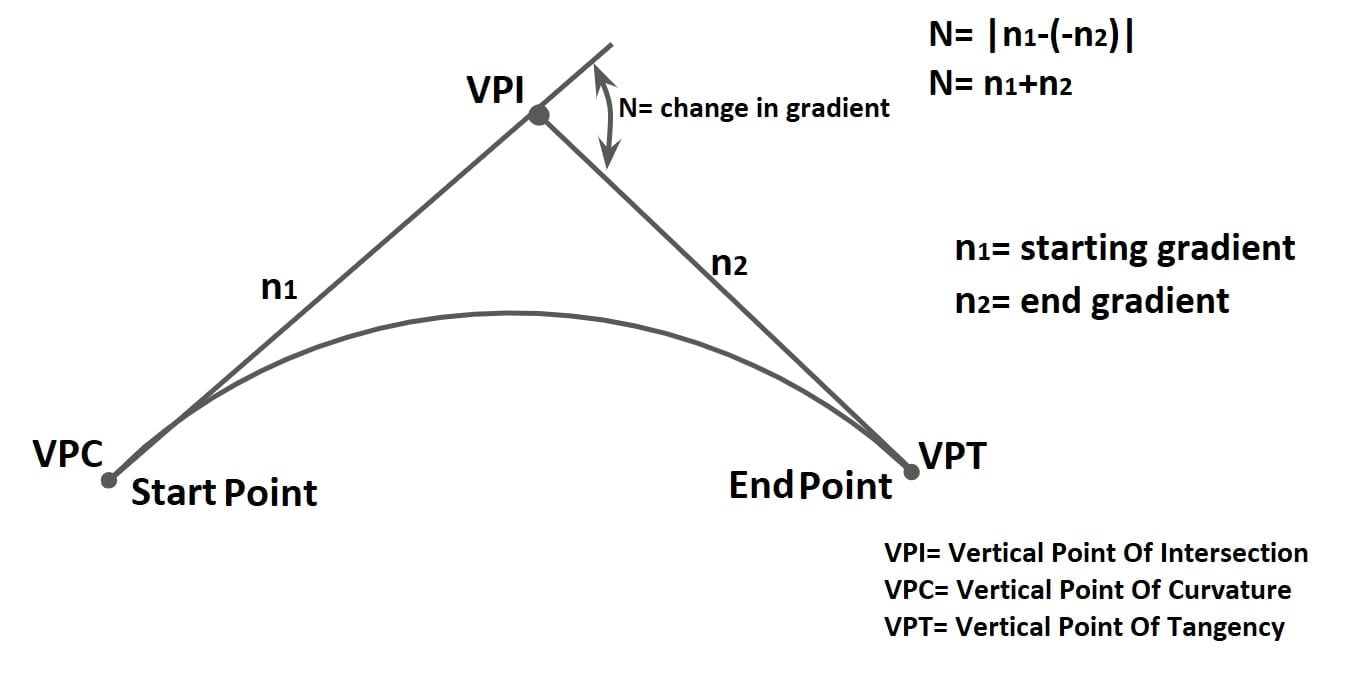
Summit curves are vertical curves with convexity upward & concavity downward.
It can formed by two gradients in the following ways.
Some Important Points of Summit Curve
- Convexity upward & Concavity downward.
- Vertical Point Of Intersection (VPI) always lies above the curve.
- Summit curve are designed only for sight distance criteria.
- Summit curve are made with square parabola shape.
- Ideal shape of summit curve is circular.
- Centrifugal force acts in upwards direction due to which effective weight of vehicle reduces. Hence there is no discomfort in summit curve.

Derivation of Summit Curve
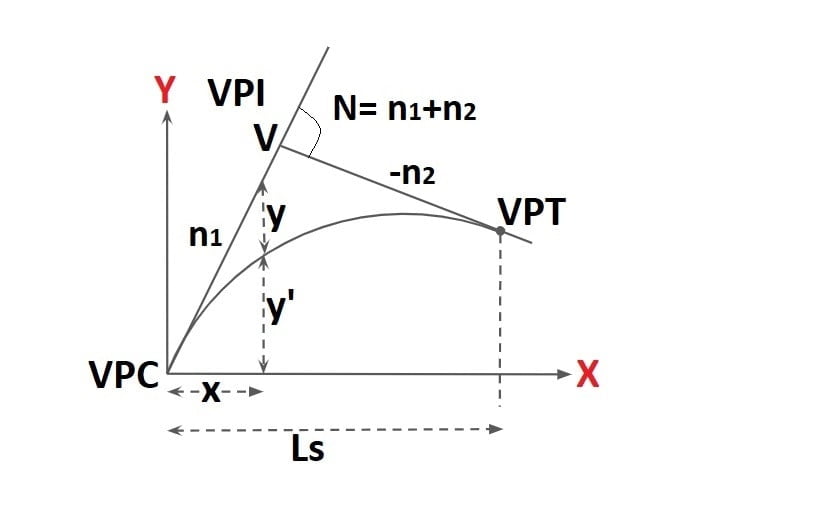
 1. General Equation of Summit Curve
1. General Equation of Summit Curve
y’= ax2 + bx + c
At point A, (y’=0, x=0)
then we put the value of (y’=0, x=0)
0= 0+0+c
c=0
y’= ax2 + bx + 0
y’= ax2 + bx
\(\frac{\mathrm{d} y’}{\mathrm{d} x}= 2ax+b\)=Gradient
At point A, x=0, \(\frac{\mathrm{d} y’}{\mathrm{d} x}= +n_1\)
+n1=2a·0+b
b=+n1
At point B, x= LS, \(\frac{\mathrm{d} y’}{\mathrm{d} x}= -n_2\)
-n2=2a·LS + n1
\(a=-[\frac{n_1+n_2}{2L_S}]\).
\(a=-[\frac{N}{2L_S}]\)
General Equation
\(y’=[-\frac{N}{2L_S}]x^{2}+n_1x\)
2. Position of Summit / Highest / Crest Point of Curve From VPC
we know that at crest point of curve, slope is zero.
\(\frac{\mathrm{d} y’}{\mathrm{d} x}=0\)2ax+b=0
x=-b/2a
we know that
b=+n1 & \(a=-[\frac{N}{2L_S}]\).
so \(x=\frac{n_1}{N}L_S\)
3. Apex Equation of Summit Curve
tanθ= n1 = (y+y’)/x
y= n1x-y’
\(y’=[-\frac{N}{2L_S}]x^{2}+n_1x\)
\(y= [n_1x-([-\frac{N}{2L_S}]x^{2}+n_1x)\)
\(y= [\frac{N}{2L_S}]x^{2}\)
4. Position pf VPI from VPC
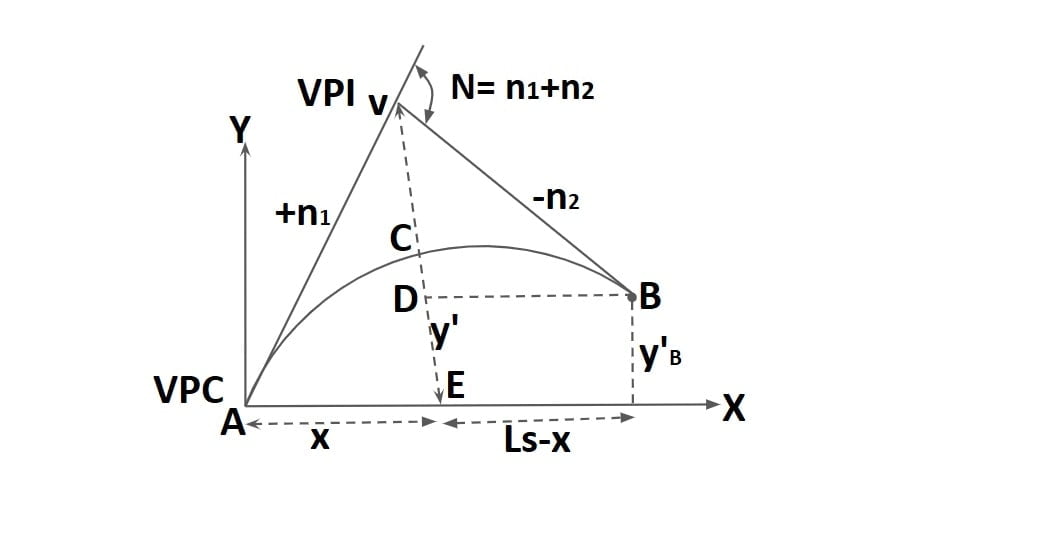 From ΔAVE
From ΔAVE
tanθ1=n1=VE/x
VE= n1x…….(1)
From ΔVDB
tanθ2=n2=VD/(LS-x)
VD= n2LS – n2x…….(2)
y’B = DE = VE- VD……..(3)
\(y’_B=[-\frac{N}{2L_S}]x^{2}+n_1x\) (x= LS) ……(4)
the value of VE, VD, y’B from equation 1,2,4 put in Equation 3.
x=LS/2
Case-1: When curve is symmetrical (n1=n2)
- Vertical line passing through VPI will bisect length of curve into two equal half.
- This line always pass through summit point of curve.
- In this case R.L of starting point & end point will be same.
Case-2: When curve is unsymmetrical (n1≠n2)
- Vertical line passing through VPI will bisect length of curve into two equal half.
- This line will never pass through summit point of curve.
- In this case the curve will be tilted & R.L of starting point & end point will be different.
5. Calculating Ordinates of Summit Curve
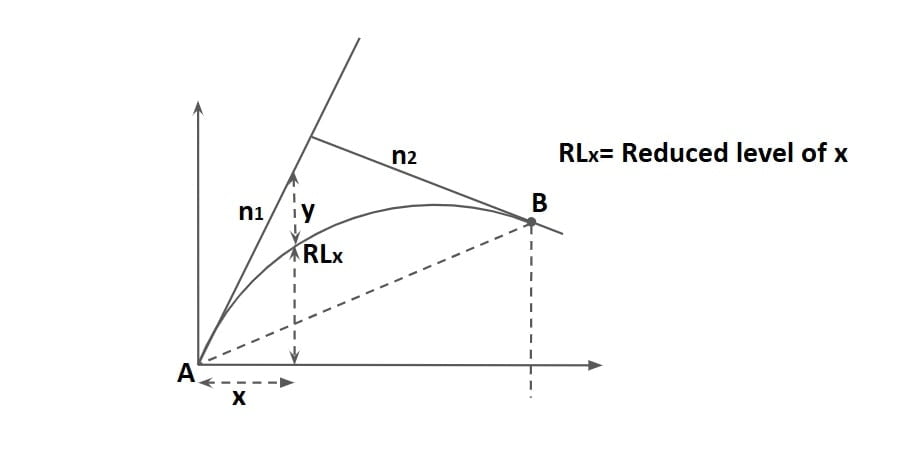 RL of a point at a distance x
RL of a point at a distance x
RLx = (RL of A) + n1x – y
RLx = (RL)A + n1x – (Nx2/2L )
RLB = (RL)A + n1L – (NL2/2L )
Length Of Summit Curve
Case-1: When LS> SD (Sight Distance)
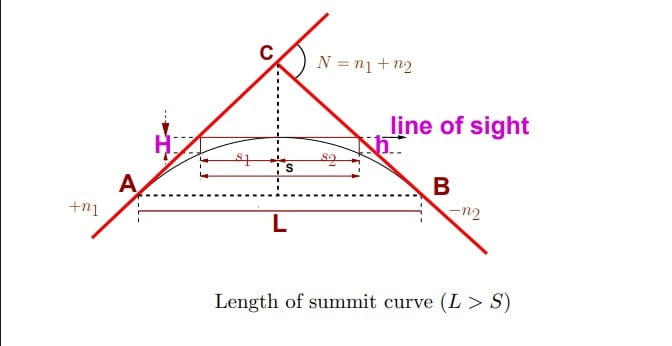 H= height of drivers eye
H= height of drivers eye
h= height of obstruction
s= sight distance
\(L_S=\frac{N\cdot s^{2}}{2(\sqrt{H}+\sqrt{h})^{2}}\).
As per IRC
for SSD, H= 1.2m, h= 0.15m.
\(L_S=\frac{N\cdot s^{2}}{4.4}\)for OSD/ISD, H=1.2m, h=1.2m.
\(L_S=\frac{N\cdot s^{2}}{9.6}\)Case-2: When LS< SD (Sight Distance)
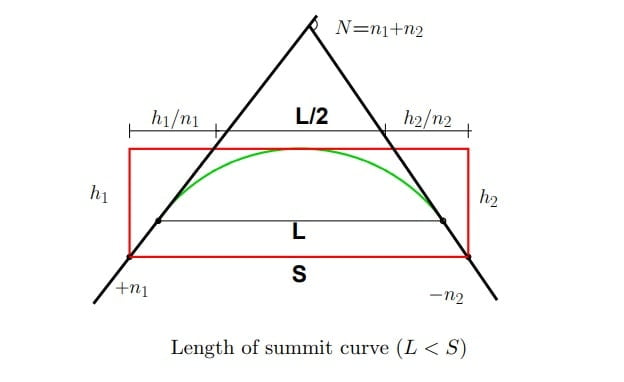 \(L_S=2s-\frac{2(\sqrt{H}+\sqrt{h})^{2}}{N}\).
\(L_S=2s-\frac{2(\sqrt{H}+\sqrt{h})^{2}}{N}\).
As per IRC
for SSD, H= 1.2m, h= 0.15m.
\(L_S=2s-\frac{4.4}{N}\)for OSD/ISD, H=1.2m, h=1.2m.
\(L_S=2s-\frac{9.6}{N}\)Note:
For calculation of sight distance in design of summit curve & valley curve, effect of gradient should not be taken.
hence
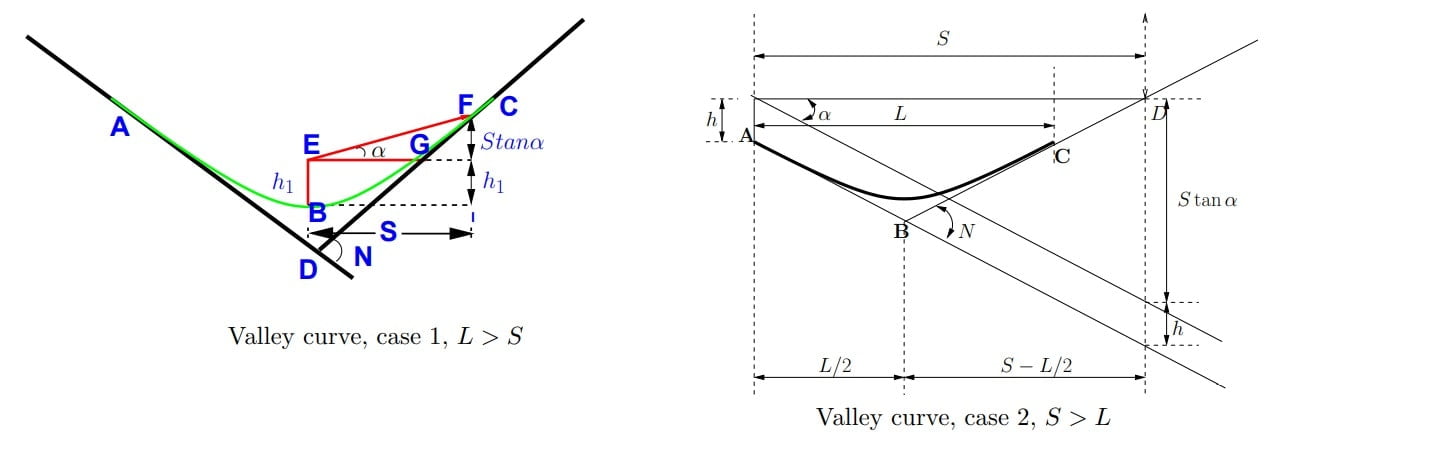
\(SSD= 0.2Vtr + \frac{V^{2}}{254f}\)Valley Curve
- Valley curve are vertical curve with concavity upward & convexity downward.
- It can formed by two gradient in following ways.

Some Important Points of Valley Curve
- Convexity downward & Concavity upward.
- Vertical Point Of Intersection (VPI) always lies below the curve.
- Valley curves are designed taking following consideration into account
- Comfort to passengers
- Headlight sight distance
- Drainage in valley curve
Note:
The maximum distance visible through the Headlight of the vehicle is called Head Light Sight Distance.
Generally HSD = SSD
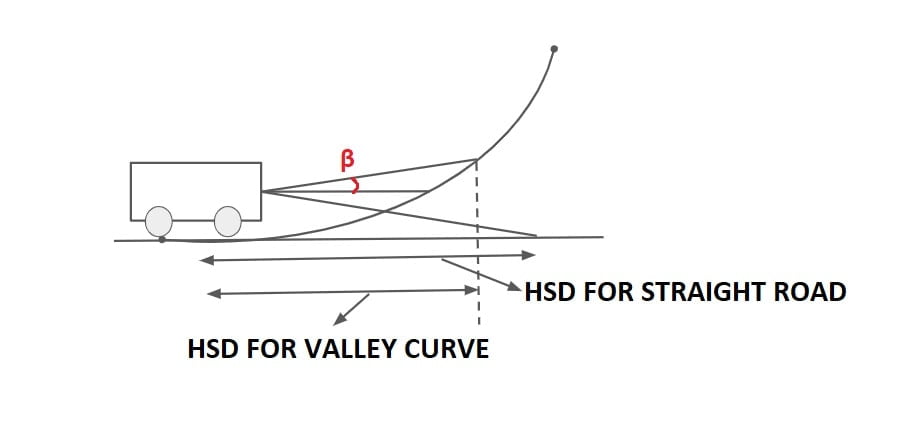 As per IRC
As per IRC
- height of head light =h=0.75m
- Beam angle = β=1°
4. Valley Curves is usually made up of two transition curve of equal length without having a circular curve in between.
5. In valley curve, centrifugal force and gravity force both acts downward, hence create discomfort for passengers.
6. Position of lowest point of valley curve from starting of curve.
\(x=L_V(\frac{n_1}{2N})^{\frac{1}{2}}\)
LV= length of valley Curve
N= Change in Gradient
n1= 1st gradient.
Length Of Valley Curve
The length of the valley curve is designed based on the max of the following two criteria.
Criteria 1: As per Comfort Condition
In this criteria the rate of change of centrifugal acceleration is limited to a comfortable zone of about 0.6m/sec3, then the length of the transition curve is given by
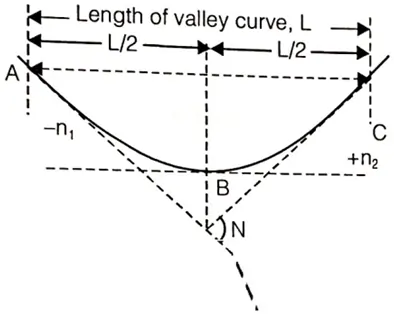
\(L_T=\frac{v^{3}}{CR}\)……(1)
and \(R=\frac{L_T}{N}\)………(2)
the value of R from equation 2 put in equation 1.
\(L_T=\sqrt{\frac{Nv^{3}}{C}}\)and LV = 2LT
\(L_V=2\sqrt{\frac{Nv^{3}}{C}}\)As per IRC
c= 0.6m/s3 for cubic parabola
v= change in speed
N = change in gradient
unit change:
\(L_V=0.378\sqrt{Nv^{3}}\)
v in kmph
LV in m
Criteria 2: As per HSD
 Case-1: When LV> HSD
Case-1: When LV> HSD
s= HSD of horizontal
β= Beam angle
h= height of headlight
\(L_V=\frac{N\cdot s^{2}}{2h+2\cdot s\cdot tan\beta }\).
As per IRC
for β=1°, h= 0.75m.
\(L_V=\frac{N\cdot s^{2}}{1.5+0.035\cdot s }\).
Case-2: When LV< HSD
\(L_V=2s -\frac{2h+2s\cdot tan\beta }{N}\).
As per IRC
for β=1°, h= 0.75m.
\(L_V=2s -\frac{1.5+0.035\cdot s}{N}\).
 1. General Equation of Summit Curve
1. General Equation of Summit Curve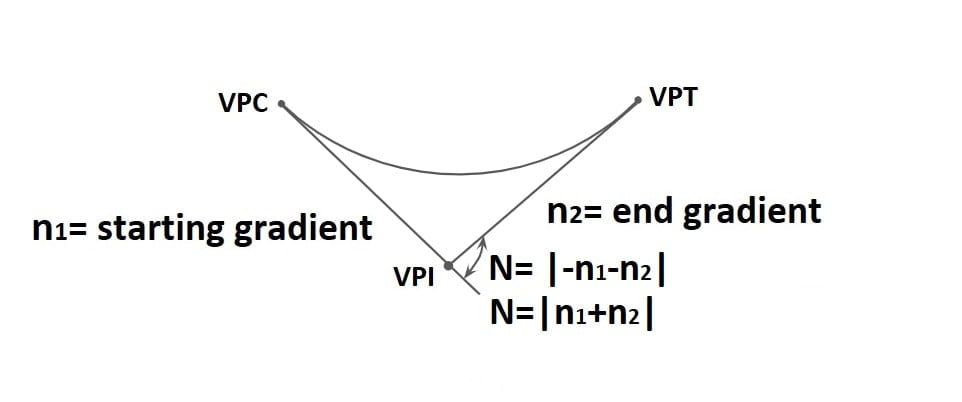
 Case-1: When LV> HSD
Case-1: When LV> HSD