In fundamentals of surveying (part-2), we details analysis about plan & map, scale, representation of scale,shrinkage ratio, type of scales & other.
Plan & Map
Plan: It is the graphical representation of various features on or near to the earth’s surface as projected on a horizontal plane. Plan represents the area on a horizontal plane. The horizontal distances are measured between the various points on the horizontal plane. Because of small areas involved in surveying as compared to earth’s total area, the areas may be regarded as flat surface and the plan is constructed by orthographic projections. A plan is usually drawn or a relatively large scale.
Map: In this, the scale of graphical projection or horizontal plane is small. Due to small scales a map depicts a large number of details as compared to plan. Some additional features are also shown on map like reliefs, contour lines, undulations etc.
Note
Distance: Linear measurement in the horizontal plane is termed as distance.
Elevation: Linear measurement in the vertical plane is termed as elevation.
SCALE
Scale is a technique through which any ground distance is represented on paper or map.
Representation of Scale
There are many way to representation of scale.
1.Engineer’s Scale
This scale is represented by a statement like 1cm = 10m ( 1cm :10m, \(\frac{1cm}{1m}\) )etc.
Here 1cm on the plan represents & 10m represents ground distance.
2.Representation Fraction (RF)
Here one unit of length on the plan represents some number of the same units of length on the ground.
Example:
1cm = 10m is represented in RF as 1:1000, \(\frac{1cm}{1000cm}\) or \(\frac{1}{1000}\)
3.Graphical Scale
If the plan or map is to be used after a few years the numerical scales (ES, RF) may not give accurate results, if the sheet or paper “Shrinks or Expands”.
In such a case, graphical scale is used in which scale is drawn on plan or map, which also shrink or expand proportionally & the distance can thus be found accurately.
Shrinkage Factor or Shrinkage Ratio
The ratio of shrunk length to the actual length is know as Shrinkage Factor (SF) or Shrinkage Ratio (SR).
Shrinkage ratio (SR) or (SF) = \(\frac{\text{Shrunk length}}{\text{Original length}}\)
Shrunk Scale = SF × Original Scale
Error Due to Shrinkage of Map
Correct distance on map in term of original scale =\(\frac{\text{measured distance on map}}{SF}\)
Correct area on map in term of original scale =\(\frac{\text{measured area on map}}{SF^{2}}\)
Correct Volume on map in term of original scale =\(\frac{\text{measured volume on map}}{SF^{3}}\)
Error Due to Wrong Measuring Scale
If a wrong measuring scale is used to measure the length or area of an already drawn line or area on the plan, the measured length or area will not be correct.
Hence it is to be correct as follows
Correct length =\(\frac{\text{RF of wrong scale × measured length}}{\text{RF of correct scale}}\)
Correct area =\(\left [ \frac{\text{RF of wrong scale}}{\text{RF of corrcet scale}} \right ]^{2}\times \)measured length
Type of Scales
Scales may be classified as follows
1. Plane Scale
It is a scale on which it is possible to measure two dimensional only units & tenth. Example (cm & m), (m & dc).
2.Diagonal Scale
On this scale, it is possible to measure three dimensions unit, tenth, & hundredth. Example (m, dm, cm)
3.Vernier Scale
It is a secondary unit of the main scale which is used to measure the dimension even lesser than the least count of the main scale.There are many type of vernier scale.
A. Direct Vernier
This vernier is calibrated in the same direction of main scale. This vernier has division slightly smaller than division of main scale.
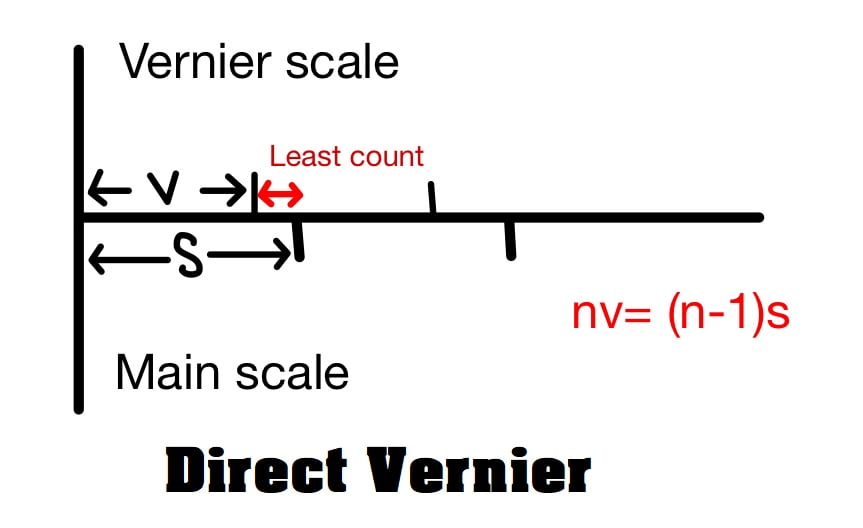
Let (n-1) division of main scale is divided into n division of vernier scale
nv=(n-1)s
v=\(\frac{(n-1)s}{n}\)
s>v
here:
s= least count of main scale (length of 1 division of main scale)
v= length of one division of vernier scale (not the least count)
Least Count (LC): The least count of the vernier is equal difference in length of one division of the main scale & one division of vernier scale.
LC= s-v = s- \(\frac{(n-1)s}{n}\)
LC= \(\frac{ns-(n-1)s}{n}\)
LC= \(\frac{s}{n}\)
B. Retrograde Vernier
This vernier is calibrated in the opposite direction of main scale. This vernier has division slightly greater than division of main scale.
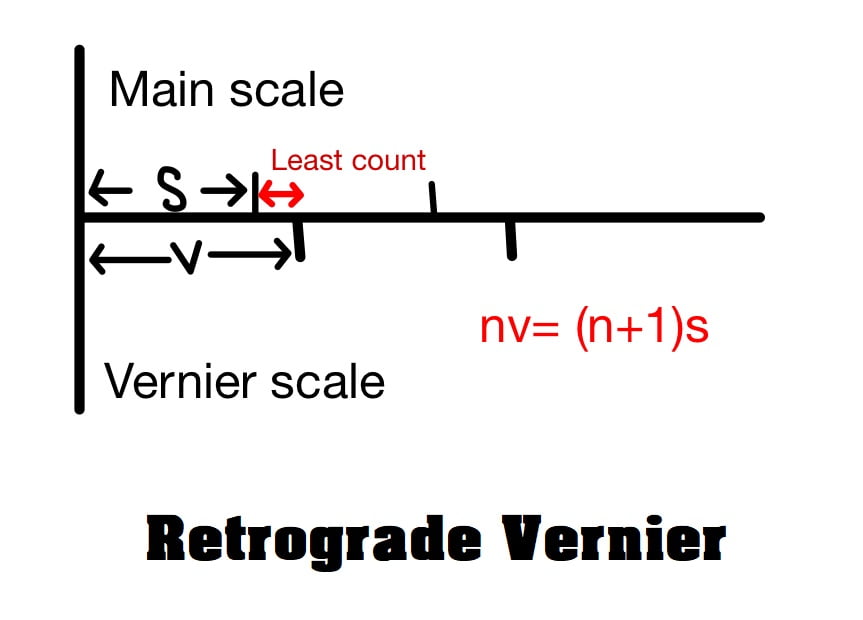
Let (n+1) division of main scale is divided into n division of vernier scale
nv=(n+1)s
v=\(\frac{(n+1)s}{n}\)
s<v
here:
s= least count of main scale (length of 1 division of main scale)
v= length of one division of vernier scale (not the least count)
Least Count (LC)
LC= v-s= \(\frac{(n+1)s}{n}\) -s
LC= \(\frac{(n+1)s-ns}{n}\)
LC= \(\frac{s}{n}\)
C. Extended Vernier
Here (2n-1) division of main scale is divided into n division of vernier scale.
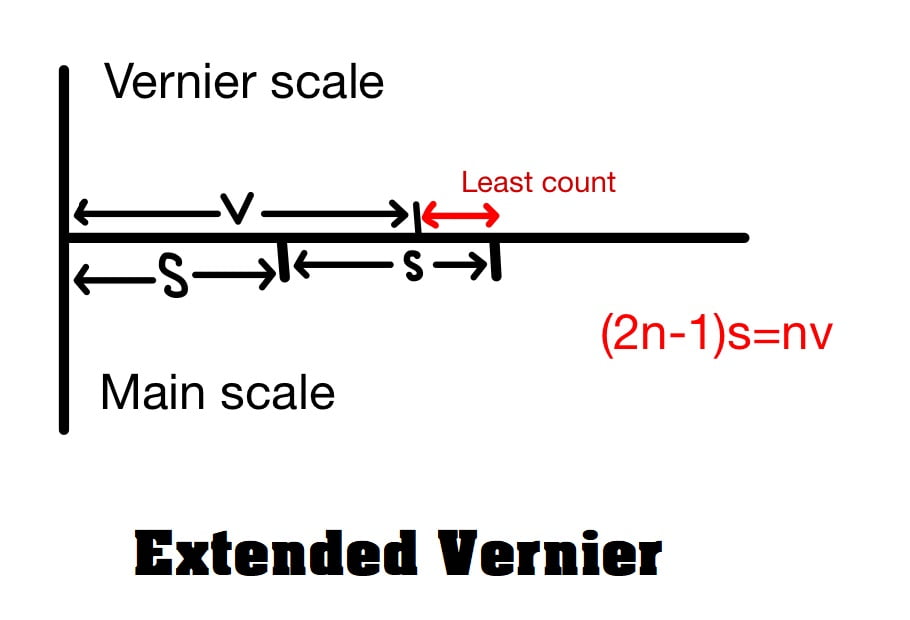
nv=(2n-1)s
v=\(\frac{(2n-1)s}{n}\)
s<v
Least Count (LC)
LC= 2s-v= 2s-\(\frac{(2n-1)s}{n}\)
LC= \(\frac{2ns-2ns+s}{n}\)
LC= \(\frac{s}{n}\)
D. Double Vernier
When the vernier is calibrated in both direction of index line it is called double vernier. To use double vernier main scale should also be calibrated in both direction.
Here also LC= \(\frac{s}{n}\)
Note: Least Count of theodolite is 20″ (20 second)