Curve  

1. The curves are the transitions which are provided at the intersection of two straight lines.
2. If curves are provided at the intersection of two straight lines in a horizontal plane it is termed as horizontal curve. And if it is provided at the intersection of two straight lines in a vertical plane it is termed as a vertical curve.
3. Horizontal curves provided are generally circular, and vertical curves provided are generally parabolic.

  Horizontal curves are generally of three types  

1. Simple Circular Curve
2. Compound Curve 
3. Reverse Curve

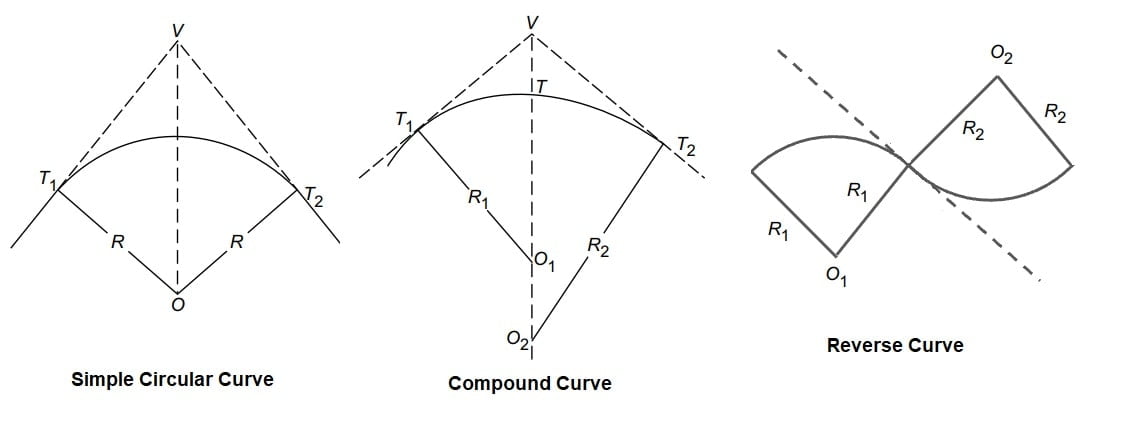
Simple Circular Curve

A simple circular curve consists of an arc of the circle. This curve is tangential to two straight lines of the route.

Compound Curve 

A compound curve consists of two circular arcs of different radius with their centres of curvature on the same side of the common tangent.

Reverse Curve

A reverse curve consists of two circular arcs (either of same or different radius) with their centres of curvature on the opposite side of the common tangent. Reverse curves are provided on the routes when the two straight lines are parallel or when angle between them is very small, for example hilly roads.

Note :

Compound and Reverse curves are provided for low speed, roads and railways.

Broken-back Curve

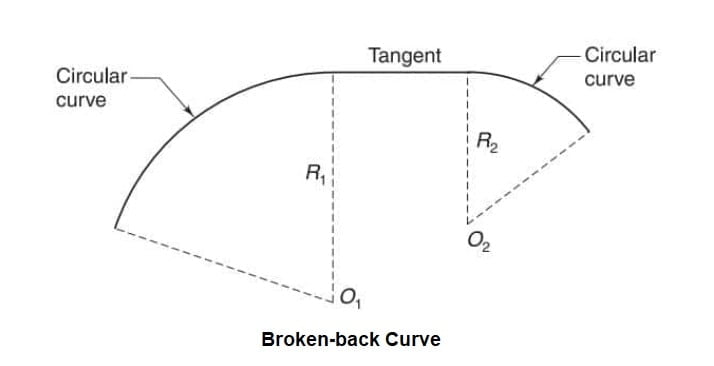
In the past, sometimes, two circular curves having their centres on the same side (Fig. 11.5) and connected with a short tangent length were used for railroad traffic. Since these are not suitable for high speeds, they are not in use nowadays.

  Basic Definitions 

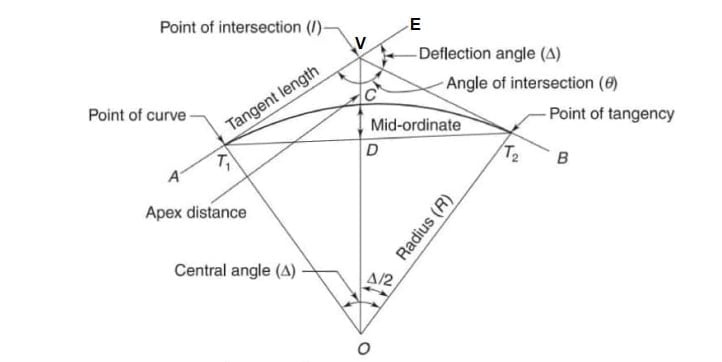
Back tangent

The tangent line before the beginning of the curve is called the back tangent or the rear tangent. The line AT₁ is the back tangent.

Forward tangent

The tangent line after the end of the curve is called the forward tangent. The line T_₂B is the forward tangent.

Vertex or point of intersection

The back tangent and the forward tangent, when extended, intersect at a point called the vertex (V) or the point of intersection (P.I.).

Deflection angle

The angle VEB is called the angle of deflection (Δ).

Point of Curvature (P.C.)

It is the point on the back tangent at the beginning of the curve. At this point, the alignment of the route changes from a straight line to a curve. The point is also called the tangent-curve (T.C.) point. The point of curvature is also called the point of curve. Point (T_₁).

Point of tangency (P.T.)

It is the point on the forward tangent at the end of the curve. At this point, the alignment of the route changes from a curve to a straight line. The point is also known as the curve-tangent (C.T.). Point (T_₂).

Tangent distance (T)

It is the distance between the point of curvature (T) to the point of intersection (V). It is also equal to, the distance between the point of intersection to the point of tangency (T₂).

External distance (E)

It is the distance (VC) between the point of intersection (V) and the middle point C of the curve.

Long chord (L)

It is the chord of the circular curve. It joins the point of curvature (T₁) and the point of tangency (T₂)=T₁DT₂ .

Mid ordinate (M)

It is the distance (CD) between the middle point (C) of the curve and the middle point (D) of the long chord.

Length of curve (l)

It is the length of the curve (or route= T₁CT₂) between the point of curvature (T₁) and the point of tangency (T₂).

  Elements of Circular Curve  

Length of Tangent (T)

Length of Tangent (T) = T₁V = VT₂ = R·tanΔ/2

T₁V = OT₁·tanΔ/2 = R·tanΔ/2

VT2 = OT₂·tanΔ/2 = R·tanΔ/2

Length of Curve (l)

Length of Curve (l) = T₁CT₂ = l

l = Δ × (π/180) × R,  Δ is in degree.

And we know that

• • Length of an Arc = Δ × R, where Δ is in radian.
  • Length of an Arc = Δ × (π/180) × R, where Δ is in degree.
  • Δ = Center angle of the arc
  • R = Radius of the circle

Mid Ordinate (M)

Mid Ordinate (M) = CD

M = CD = OC- OD

\(M=R-Rcos\frac{\Delta }{2}\).

\(M=R(1-cos\frac{\Delta }{2})\).

\(M=R(versine\frac{\Delta }{2})\).

The mid ordinate of the curve is also called as the versine of the curve.

Length of Chord (L)

Length of Chord = T₁DT₂ =T₁D + T₂D

L = R·sinΔ/2 + R·sinΔ/2

L = 2·R·sinΔ/2 

External Distance (E) Apex Distance

E = VC = OV-OC

{In triangle T₁VO, cosΔ/2 = T₁O/OC

secΔ/2 = OC/ T1O

secΔ/2 = OC/ R

R•secΔ/2 = OC}

E = R·secΔ/2 – R

E = R·(secΔ/2 – 1)

Chainage of Tangent points

Chainage at T₁ = Chainage at V – length of tangent.

Chainage at T₂ = Chainage at T₁ + length of Curve.

Intermediate Chord Length

For 1_st chord

C₁ = {Multiple of chain length just greater than chainage at T₁ – Chainage at T₁ }

For 2_nd to (n-1) chord

C₂ = C₃ = C₄ ………= C_n-1 = {chain length= C}

For Last chord

C_n = {Chainage at T2– Multiple of chain length just less than chainage at T2 }

No of Intermediate Chord

\(n=[\frac{l-C_1-C_2}{\text{chain length}}+2]\)

FOR MORE INFORMATION ABOUT SURVEYING