Setting Out Of Circular Curve 

It is the process of locating the point along the length of curve either at equal or convenient distance.

Setting of curve can be broadly done by two method.

1. Linear Method

• These are the methods in which setting is done by measuring distances.

2. Angular Method

• These are method in which setting is done by measuring angles with or without measuring distances.

Method of setting of curve is also classified on the basic of Instrument Used.

1. Tape Method
2. Tape & Theodolite Method
3. Two Theodolite Method
4. Tacheometric Method
5. Total Station Method

---

Linear Method

The following are the linear methods which can be used for setting circular
curves:
(i) Offsets From Long Chord
(ii) Perpendicular Offset From Tangent
(iii) Offset From Chord Produced
(iv) Radial Offset From Tangent
(v) Successive Bisection Of Chords

In these methods only linear measurements are taken. Hence, the
surveyor needs chain/tape.

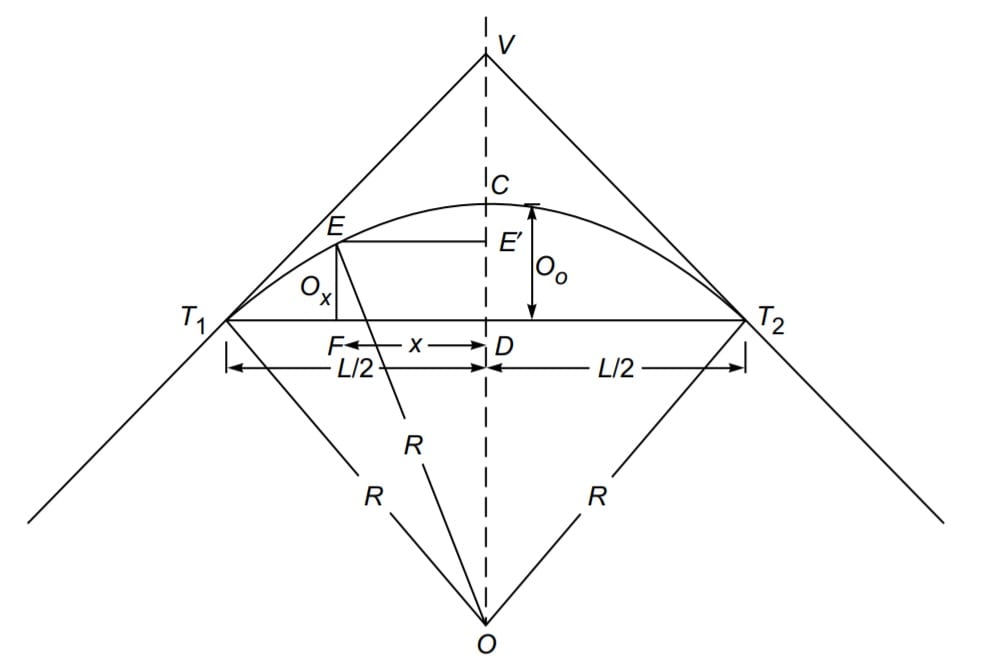
1.Offsets From Long Chord

R – radius of the curve
L – length of long chord
O0 – mid-ordinate = CD
Ox – ordinate at distance x from the mid-point of long chord

CD = OC – OD

OC = OT₁= R

In Δ OT₁D

OD² =OT₁² -T₁D²

\(OD = \sqrt{R^{2}-(\frac{L}{2})^{2}}\).

\(CD = R^{2}-\sqrt{R^{2}-(\frac{L}{2})^{2}}\)

In Δ E’EO

OE² =EE’² + OE’²

\(R^{2}=x^{2}+(OD+O_x)^{2}\).

\((OD+O_x)^{2}=R^{2}-x^{2}\).

\(O_x=\sqrt{R^{2}-x^{2}}-\sqrt{R^{2}-(\frac{L}{2})^{2}}\).

2.Perpendicular Offset From Tangent

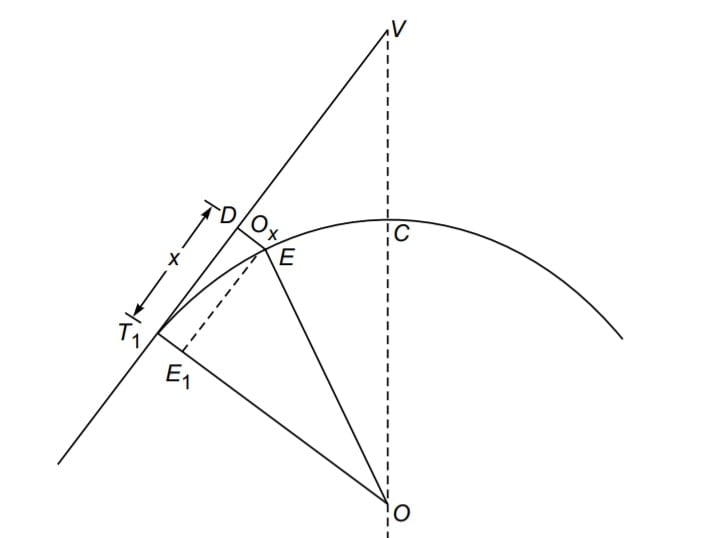
O_x= T₁E₁= T₁O- E₁O

T₁O= R

\(E_1O= {\sqrt{R^{2}-x^{2}}}\)

\(O_x=R-{\sqrt{R^{2}-x^{2}}}\).  {Exact Formula}

\(O_x=R-R(1-\frac{x^{2}}{R^{2}})^{\frac{1}{2}}\).

Expand \(R(1-\frac{x^{2}}{R^{2}})^{\frac{1}{2}}\) using binomial theorem.

then

\(O_x=\frac{x^{2}}{2R}\) (approximately)

3.Offset From Chord Produced

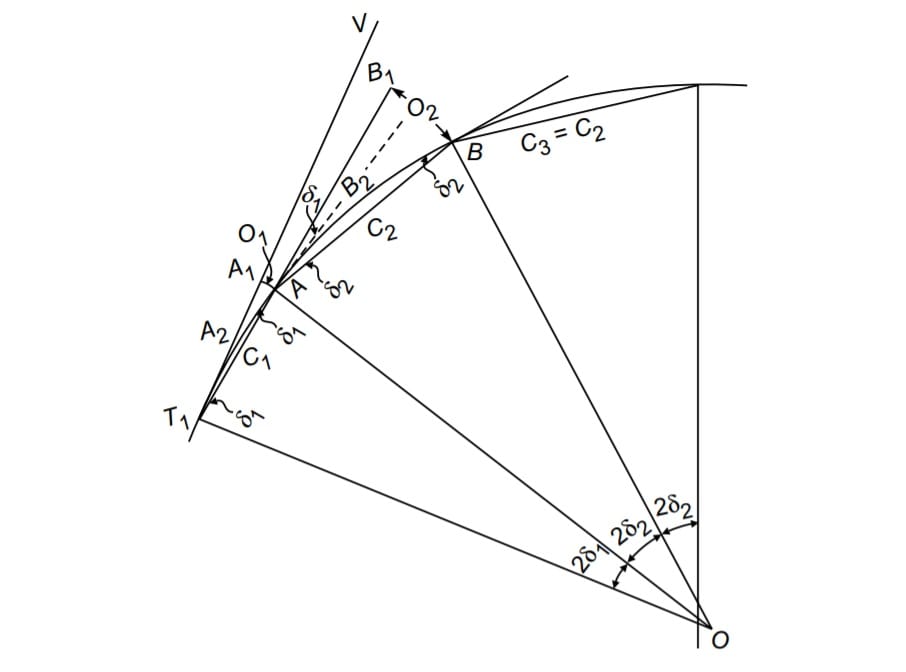
Let T₁A = C₁ be length of first sub-chord

AB = C₂ be length of full chord

δ1 = deflection angle A₁T₁A

δ2 = deflection angle B₁AB

Then from the property of circular curve

T₁OA = 2δ1

C₁ = chord T1A ≈ Arc T₁A = R·2·δ1

C₁ = R·2·δ1

\(\delta _1=\frac{C_1}{2R}\)   ….(i)

offset O₁ = arc AA₁ =C₁δ₁  ….(ii)

Substituting the value of δ₁ from equation (i) into equation (ii), we get

\(O_1=C_1\times \frac{C_1}{2R}\).

\(O_1=\frac{C_1^{2}}{2R}\).

similarly  O₂ =C₂ (δ₁+δ₂)

\(O_2=C_2(\frac{C_1}{2R}+\frac{C_2}{2R})\).

\(O_2=\frac{C_2}{2R}(C_1+C_2)\).

similarly

\(O_3=\frac{C_3}{2R}(C_2+C_3)\).

\(O_4=\frac{C_4}{2R}(C_3+C_4)\).

\(O_5=\frac{C_5}{2R}(C_4+C_5)\).

\(O_n=\frac{C_n}{2R}(C_{n-1}+C_n)\).

but C₂ =C₃ =C_{4 ………..}=C_n-1 = C= chain length

Thus, upto last full chord i.e. n – 1 the chord,

so

\(O_1=\frac{C_1^{2}}{2R}\).

\(O_2=\frac{C^{2}+C_1C}{2R}\).

\(O_3=O_4….=O_{n-1}=\frac{C^{2}}{R}\).

\(O_n=\frac{C\cdot C_n+C_n^{2}}{2R}\)

This method is the best method for longer curves of larger radius by linear method & is usually used when theodolite is not available.

It has advantage that, not all the land between tangents and curve need to be accessible.

4.Radial Offset From Tangent

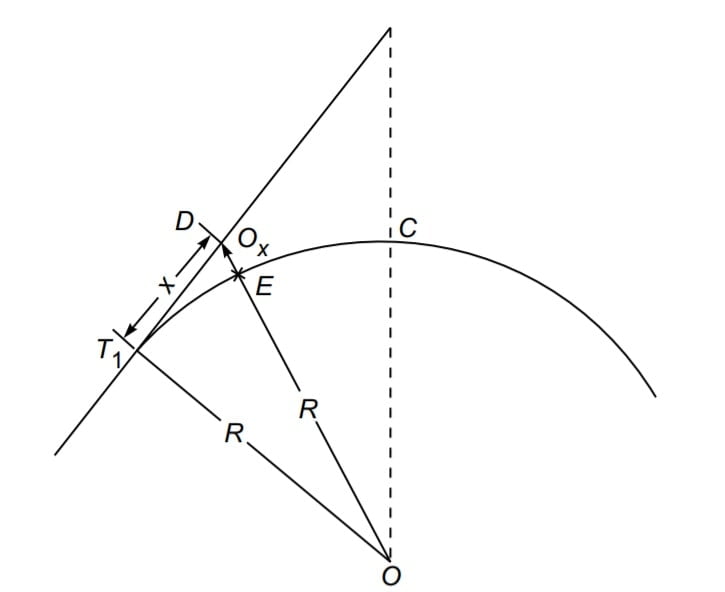
From Δ OT₁D, we get

OD² = OT₁²+ T₁D²

(R + Ox)² = R²+ x²

O_x + R = (R² +x² )^½

O_x = (R² +x² )^½ – R  {Exact Formula}

\(O_x=R\sqrt{1+(\frac{x}{R})^{2}}-R\).

\(O_x=R(1+\frac{x^{2}}{2R^{2}}-\frac{x^{2}}{8R^{4}})-R\)  …….using binomial theorem.

Neglecting small quantities of higher order,

\(O_x=R(1+\frac{x^{2}}{2R^{2}})-R\).

\(O_x=\frac{x^{2}}{2R}\).   {Approximate Formula}

---

Angular Method

The following are the angular methods which can be used for setting circular
curves:
(i) Tape & Theodolite/Rankine Method / Tangential / Deflection Angles.
(ii) Two-theodolite Method
(iii) Tacheometric Method
In these methods linear as well as angular measurements are used. Hence, the
surveyor needs chain/tape and instruments to measure angles. Theodolite is the
commonly used instrument. These methods are briefly explained in this chapter.

Tape & Theodolite/Rankine Method / Tangential / Deflection Angles

• In this method tape is used for making linear measurement and theodolite is used for making angular measurement.
• For this method it is recommended that chord length done not exceed (R/20) as this ensure that length of chord may be approximated to the corresponding length of arc.

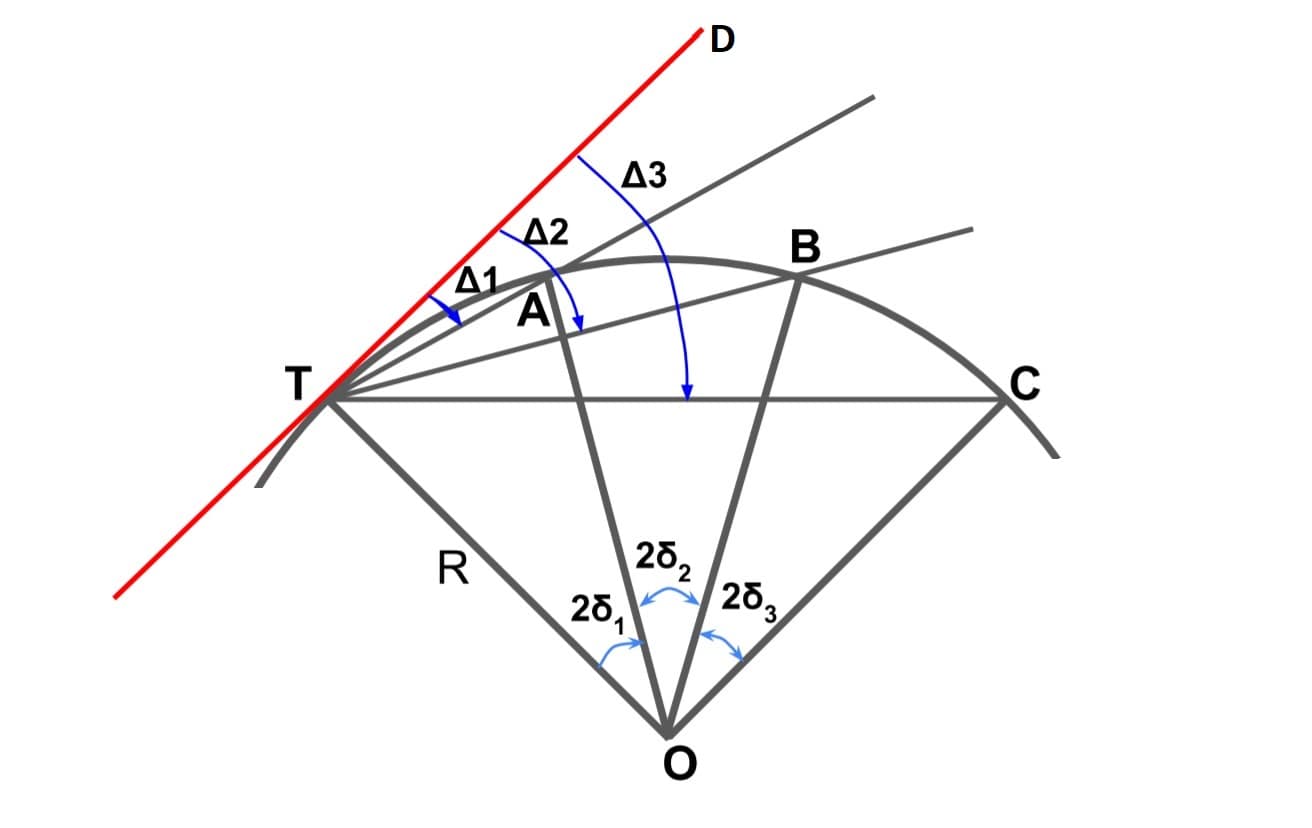
OT= OA= OB= OC= R

In triangle OTA

∠OTA = ∠OAT  (∴OT= OA =R ) 

Assume ∠OTA = ∠OAT = θ

so ∠OTA + ∠OAT + ∠AOT  =180°

θ+θ+2δ₁ =180°  (∴∠AOT=2δ₁ ) 

2θ+2δ₁ =180°

 θ =90° – δ1  ….(i)

we know that line TD is the tangent line of OT so ∠OTD =90°

and ∠ATD = Δ₁ , ∠OTA = θ

∠OTD = ∠OTA + ∠ATD =90°

 θ + Δ₁ =90° 

we put the value of  θ from equation 1

90° – δ1  + Δ₁ =90°

Δ₁ = δ1

so deflection angle

Δ₁ =δ1

Δ₂ = δ₁+δ₂ = Δ₁ +δ₂ 

Δ₃ = δ₁+δ₂+δ₃= Δ₂ +δ₃ 

so on

Δ_n = Δ_n-1 +δn 

For δ calculation from Arc

\(2\delta _1=\frac{C_1}{R} \) ….(Radian)

\(\delta _1=\frac{C_1}{2R}\)  ….(Radian)

\(\delta _1=\frac{90C_1}{\Pi R} \) ….(degree)

\(\delta _2=\frac{90C_2}{\Pi R} \).

so on

\(\delta _n=\frac{90C_n}{\Pi R} \)

Here  δ₁, δ₂, δ₃,…..δ_n  are the tangential angle made by successive chords TA, AB,BC… with their respective tangents.

Here  Δ₁, Δ₂, Δ₃,…..Δ_n  are the deflection angle made by successive chords TA, TB, TC… with back tangent at T.

Two-theodolite Method

 

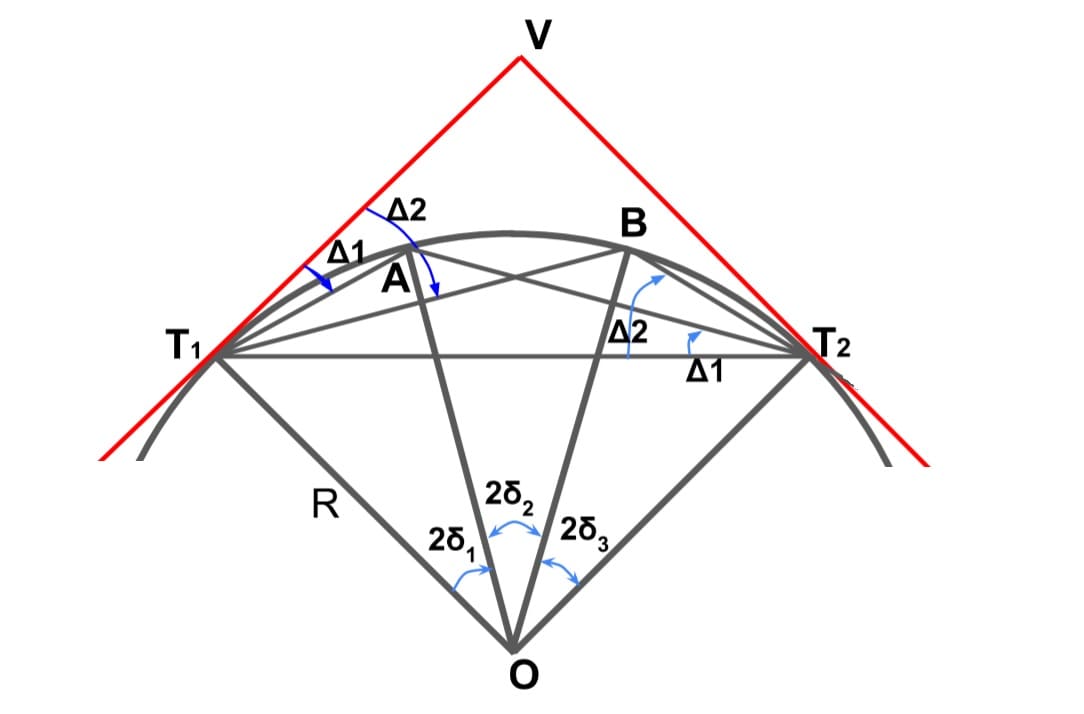
Δ₁ =δ1

Δ₂ = δ₁+δ₂ = Δ₁ +δ₂ 

Δ₃ = δ₁+δ₂+δ₃= Δ₂ +δ₃ 

so on

Δ_n = Δ_n-1 +δn 

• In this theodolite are used for angular measurement and no linear measurement is being carried out.
• One of the theodolite is placed at T1 and other at T2.
• It is suitable to be used when taping/ chaining is difficult i.e where ground is rough.
• In this method the error in setting out is not carried forward as each point is fixed independently.
• This method is based upon the property of the circle that chord makes an angle at the center of circle which is twice the angle made by chord any other point on the circle.
• Hence, it can be concluded that the angle made by the chord with the tangent at a point is equal to the angle which chord subtends at any other point on circle.

Tachometer Method 

• In this case both linear & angular measurement is done by tachometer.
• Here process is similar to tape & theodolite method.